Головна ⇒ 📌Математика ⇒ СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

РОЗДІЛ II ОДНОЧЛЕНИ

&5. СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

Подивіться на малюнки 3 і 4. Ви бачите квадрат зі стороною а (мал. 3) і куб з ребром а (мал. 4). Ви знаєте, як знайти площу квадрата й об’єм куба та як записати результат за допомогою відповідних виразів: а2 і а3.

Узагалі, добуток n рівних множників, кожний з яких дорівнює а, можна записати за допомогою степеня:

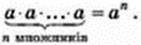
СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

Мал. 3

У виразі аn число и називають основою степеня. Воно показує, яке число множили саме на себе. Число n

називають показником степеня. Він показує, скільки рівних множників було в добутку. Оскільки для лічби множників використовують натуральні числа, то виразу an дали назву “степінь з натуральним показником”. Пізніше ви дізнаєтеся про степені з іншими показниками.

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

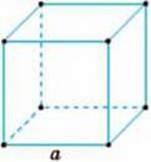
Мал. 4

Степенем числа а з натуральним показником n, більшим за 1, називається добуток л множників, кожний із яких дорівнює а.

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

Вираз аn читають так: “а в степені n” або “енний степінь числа а”.

Задача 1. Запишіть вираз 27 ∙ 3 ∙ 9 у вигляді степеня з основою:

1)3; 2) 9; 3)27.

Розв’язання.

1)27

∙ 3 ∙ 9 = 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 36;

2) 27 ∙ 3 ∙ 9 = 9 ∙ 3 ∙ 3 ∙ 9 = 9 ∙ 9 ∙ 9 = 93;

? Чому в означення степеня з натуральним показником не включено показник 1? Тому що немає сенсу говорити про добуток, у якому лише один множник. Степінь із показником 1 визначають окремо.

Запам’ятайте!

Степенем числа а з показником 1 називається саме число а.

А1 =а

Якщо основа степеня дорівнює 1, то значення степеня за будь-якого натурального n дорівнює 1:

1n = 1.

Якщо основа степеня дорівнює 0, то значення степеня за будь-якого натурального n дорівнює 0:

0n = 0.

Задача 2. Розв’яжіть рівняння: (х + 5)2=0.

Розв’язання. (х + 5)2=0, (х + 5) ∙ (х + 5) = 0, х + 5 = 0, х=-5.

Зверніть увагу:

Якщо значення степеня з натуральним показником дорівнює 0, то основа степеня дорівнює 0. Тобто, якщо аn = 0, то а = 0.

Задача 3. Чи є рівними значення степенів:

1)54 I (-5)4; 2) 53 і (-5)3?

Розв’язання. Обчислимо значення даних виразів:

1) 54 = 5 ∙ 5 ∙ 5 ∙ 5 = 625, (-5)4= (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625;

Отже, 54=(-5)4.

2) 53 = 5 ∙ 5 ∙ 5 = 125, (-5)3= (-5) ∙ (-5) ∙ (-5)= 125.

Отже, 53 ≠ (-5)3.

Знак степеня залежить від знака основи степеня та від парності чи непарності показника степеня. Як ми побачили в задачі 3, добуток парної кількості від’ємних чисел є додатним, а добуток непарної кількості від’ємних чисел є від’ємним. Добуток будь-якої ковкості (як парної, так і непарної) додатних чисел є додатним.

Зверніть увагу:

1) будь-який натуральний степінь додатного числа число додатне:

Аn > 0, якщо а > 0, n – натуральне число;

2) парний натуральний степінь від’ємного числа число додатне:

Аn > 0, якщо а < 0, n = 2k, k – натуральне число;

3) непарний натуральний степінь від’ємного числа число від’ємне:

Аn < 0, якщо а < 0, n = 2k – 1, k – натуральне число.

Дію, за допомогою якої добуток рівних множників згортають у степінь, називають піднесенням до степеня. Це – п’ята арифметична дія, яка є дією третього ступеня. Під час обчислення значень виразів її виконують найпершою.

Задача 4. Обчисліть значення виразу 5х2 + 10 для х = -3.

Розв’язання. Підставимо у вираз 5х2 + 10 значення змінної -3:

5х2 + 10 =

= 5 ∙ (-3)2+ 10 =

= 5 ∙ 9 + 10 =

= 55.

Зверніть увагу:

У виразах, що містять степені, спочатку виконують піднесення до степеня, а потім – множення, ділення, додавання, віднімання.

Дізнайтеся більше

Уперше натуральні степені чисел охарактеризував Діофант Александрійський. У своїй знаменитій “Арифметиці” він описує перші натуральні степені чисел так: “Серед чисел є квадрати, що отримані множенням числа самого на себе, ці числа називаються стороною квадрата; куби, що отримані множенням квадратів на їх сторону; квадрато-квадрати – від множення квадратів самих на себе; квадрато-куби, що отримані множенням квадрата на куб його сторони; кубо-куби – від множення кубів самих на себе”.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Що таке степінь числа; основа степеня; показник степеня?

2. Що означає піднести число а до степеня n?

3. Чому дорівнює а в степені 1?

4. Чому дорівнює 1 в степені n?

5. Чому дорівнює 0 в степені n?

6. Який знак парного степеня додатного числа; від’ємного числа?

7. Який знак непарного степеня додатного числа; від’ємного числа?

8. Який порядок виконання дій у виразі, що містить степені?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

170. Чи правильно, що вираз аn – це: 1) добуток чисел а і n; 2) а-ий степінь числа n; 3) n-ий степінь числа а?

171. Чи правильно, що у виразі аn число а показує: 1) скільки рівних множників було в добутку; 2) яке число множили саме на себе?

Як називається число а?

172. Чи правильно, що у виразі аn число ге показує: 1) яке число множили саме на себе; 2) скільки рівних множників було в добутку?

Як називається число n?

173. Прочитайте вираз:

1)22;

2) (-10)3;

3)1,210;

4) (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)4;

5)(-5)5;

6)02

Назвіть основу і показник степеня. Що вони показують?

174. Скільки разів взято множником число 0,5, якщо отримали степінь:

1) 0,52; 2) 0,55; 3) 0,5n; 4) 0,5m?

175. Запишіть у вигляді степеня:

1)2 ∙ 2 ∙ 2;

2) (-7) ∙ (-7) ∙ (-7) ∙ (-7) ∙ (-7);

3) (-1,5) ∙ (-1,5) ∙ (-1,5) ∙ (-1.5).

176. Запишіть у вигляді добутку:

1) (-15)5;

2) 104;

3) (-4)6.

177. Якими даними треба доповнити порожні клітинки таблиці 4?

Таблиця 4

Степінь

22

78

(-2,5)3

44

Основа степеня

-5

0

0,9

1

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

-9

Показник степеня

6

3

10

2

14

3

178. Ми є правильною рівність: 1) 1n = -1; 2) 0n = n; 3) 0n = 0; 4) 1n = 1?

179. Обчисліть: 1) 06; 2) 015; 3) 19; 4) 1100.

180. Чи правильно, що для від’ємного числа а:

1) аn – від’ємне число;

2) аn – від’ємне число, якщо n – парне натуральне число;

3) аn – від’ємне число, якщо n – непарне натуральне число;

4) аn – додатне число;

5) аn – додатне число, якщо n – непарне натуральне число;

6) аn – додатне число, якщо n – парне натуральне число?

181.Чи правильно, що у виразах, які містять степені, спочатку виконують: 1) додавання; 2) віднімання; 3) множення; 4) ділення; 5) піднесення до степеня?

182. Запишіть у вигляді степеня:

1) (-n) ∙ (-n) ∙ (-n) ∙ (-n) ∙ (-n) ∙ (-n) ∙ (-n) ∙ (-n) ∙ (-n);

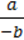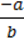2) – СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ ∙ СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ ∙ СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ;

3) 2а ∙ 2а ∙ 2а ∙ 2а ∙ 2а ∙ 2а ∙ 2а ∙ 2а ∙ 2а.

183. Обчисліть:

1)26; 6) (-2)3; 11) (1СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)2;

2) (-1,1)2; 7) (-3)3; 12) (-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)4 .

3)(-4)2; 8)33;

4)0,14; 9)(-0,2)6;

5) 0,53; 10) (-5)3;

184. Обчисліть:

1) 0,43;

2) (-6)4;

3) (-25)1;

4) (-0,1)5;

5) -(1СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)2;

6) (-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)4.

185. Знайдіть а2, якщо а дорівнює: 1) 10; 2) -0,1; 3) -4; 4) –СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ.

186. Знайдіть m3, якщо m дорівнює: 1) 10; 2) -0,1; 3) -4; 4) СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ.

187. Знайдіть:

1) суму квадратів чисел 5, -2 і -4;

2) різницю кубів чисел -10 і 5;

3) суму квадрата числа 6 і четвертого степеня числа -3.

188. Знайдіть:

1) суму квадратів чисел -1, 6 і -3;

2) квадрат суми чисел -1, 6 і -3;

3) різницю кубів чисел 5 і -7;

4) куб різниці чисел 5 і -7.

189. Запишіть у вигляді степеня число: 1)4; 2) 9; 3) 16; 4) 5. Скільки розв’язків має задача?

190. Запишіть у вигляді степеня число: 1) 100; 2) 49; 3) 64; 4) 2. Скільки розв’язків має задача?

191. Обчисліть:

1) 03; 3) 071; 5) 13 + 022;

2) 112; 4)-1111; 6)05 – (-1)9.

192. Розв’яжіть рівняння:

1) х5 = 0; 3)(-х)2=0; 5) (6 + 5х)26= 0;

2) (х + 1)3 = 0; 4) (8 – х)9 = 0; 6) (4х + 20)111 = 0.

193. Розв’яжіть рівняння:

1) х8 = 0;

2)(15 + х)13 = 0;

3)(9 – 6х)2 = 0;

4)(0,1х + 8)17 = 0.

194. Додатним чи від’ємним є значення степеня:

1)(-8)8;

2)107;

3) (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)7;

4) (-3,6)5;

5) (-1)9;

6) (-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)6?

195. Поставте знак <, >, = між виразами:

1) 123 і 0; 4)123 і (-1)32; 7) (-2)6 і 26;

2) (-2)5 і (-5)2; 5) 231 і 321; 8) -26 і 26; 10) 0,53 і (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)3 ;

3) (-7,2)5 і 03; 6) 80 і 34; 9) -26 і (-2)6;

11) -0,26 і (-0,2) ∙ (-0,2) ∙ (-0,2) ∙ (-0,2) ∙ (-0,2) ∙ (-0,2).

196. Порівняйте значення виразів:

1) (-4)4 і 44; 3)(-1)5 і 15; 5) (-1)6 і 16;

2) (-4)3 і 43; 4) 17 і 19; 6) 03 і 011.

197. Обчисліть:

1)111 ∙ (-1)11; 3) -(-3)4 + 34+ 103 ∙ 16;

2)01 ∙ (-4)2 : (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)4; 4) (-1)3 ∙ (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)2 ∙ 120.

198. Обчисліть:

1) 343 ∙ 012; 3) -(-1)3 + 52 – 24;

2)-(-2)5 – 25 + 13 ∙ 31; 4) (-16)3 ∙ (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)2 ∙ 04

199. Обчисліть:

1) (-6)3+(-62) ∙ 3; 3) -6 + 6 ∙ З2;

2) (-63 + 62) ∙ 3; 4) -6 + (-6) ∙ 32.

200. Обчисліть:

1) (-10)3+ (-12); 3)(-12 + 82) : (-2);

2) ((-5)3 + 52) : 10; 4) (-12 + 8)2 ∙ (-2).

201. Розв’яжіть рівняння:

1)2 ∙ 32 – х = 25;

2)4х = 82;

3)34 + х = (-9)2

202. Запишіть у вигляді степеня з основою 5:

1) 25 ∙ 5;

2) 5 ∙ 25 ∙ 125;

3) 25 ∙ 25 ∙ 125 ∙ 125 ∙ 125 ∙ 25.

203. Запишіть у вигляді степеня з основою 2:

1)8 ∙ 4;

2)2 ∙ 4 ∙ 16;

3)32 ∙ 2 ∙ 64.

204. Запишіть вираз 4 ∙ 64 ∙ 16 у вигляді степеня з основою:

1)2; 2)4; 3)16.

205. Запишіть вираз 2 ∙ 8 ∙ 16 у вигляді степеня з основою:

1)2; 2)4; 3)16.

206. Знайдіть а4, якщо а дорівнює: 1) -2; 2) -0,3; 3) СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ .

207. Знайдіть m5, якщо m дорівнює: 1) 0,2; 2) -3; 3) –СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ.

208. Знайдіть значення виразу (а + b)2, якщо:

1) а = 2, b = -2,1;

2) а = СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ, b = -1СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ;

3) а = СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ, b = 2,2.

209. Знайдіть значення виразу а2 + b2, якщо:

1) а = 2, b = -2,1;

2) а =-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ , b = -1СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ;

3) а = 1, b = -2,2

210. Знайдіть різницю куба суми квадратів чисел -2 і 3 та квадрата суми кубів цих чисел.

211. Знайдіть число, квадрат якого дорівнює:

1)0,16;

2)0,0025;

3) СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ;

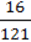4) 1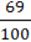СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ.

212. Куб якого числа дорівнює:

1) -8;

2) 0,125;

3)-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

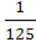
213. Обчисліть:

1) -3 ∙ (-5)3 + 12 ∙ (-14)2 – 44 ∙ 32;

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

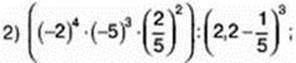
3) -23 ∙ (-5)2 ∙ (-22) ∙ (-5)3 ∙ (64 – 82)7.

214. Обчисліть:

1) 0,52 + (-0,1 )2 ∙ 63; 3) (-0,4)2 + 0,32 ∙ (-1 )3 + З2;

2) (0,52 + (-0,1 )2) – 63; 4) ((-0,4)2 + 0,32) ∙ ((-1 )3 + 32).

215. Число 9065 можна записати як суму розрядних доданків: 9065 = 9 ∙ 103 + 0 ∙ 102 + 6 ∙ 101 + 5.

Запишіть у такому вигляді число:

1)253608; 2) 22000.

216. Обчисліть:

1) 104 + 2 ∙ 103 + 3 ∙ 102 + 4 ∙ 101 + 5;

2) 5 ∙ 105 + 6 ∙ 103 + 6 ∙ 102 + 5.

217. Знайдіть суму чисел:

1) 2 ∙ 105 + 2 ∙ 104 + 2 ∙ 102 + 2 ∙ 101 + 2 і 5 ∙ 105 + 5 ∙ 104 + 5 ∙ 102 + 5 ∙ 101+ 5;

2) 9 ∙ 105 + 2 ∙ 104 + 4 ∙ 103 + 6 ∙ 101 і 5 ∙ 106 + 8 ∙ 103 + 9 ∙ 102 + 3.

218. Визначте знак виразу:

1)-(-4)15 ∙ (-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)6;

2) -95 ∙ (-СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)6;

3) (-0,01)23 ∙(-1)8 ∙ 5665

219. Запишіть у порядку зростання числа: (-0,2)2, (-0,2)3, (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)1, -(-0,2)2 і -(-0,2)3

220. Чи може а2 бути меншим, ніж а? Наведіть приклад.

221. За якого натурального значення n виконується нерівність:

1)(-6)2 < 3n < (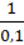СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)2;

2) 03≤ 0,5n ≤ (СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)2?

222. Розв’яжіть рівняння:

1) (1,2 – 3х)4 = 0; 5) х8 ∙ (15 – х)8 = 0;

2)(2 – х)3 = 0; 6) (7,2 + 8х)5 ∙ (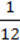СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ – 2х)2 = 0;

3) 23 ∙ х3 ∙ (-х)3=0; 7) |x – 5| ∙ (х – 6)99 = 0;

4) (1 – х)6 ∙ (9 + х)12 = 0; 8) | х + 1|3 ∙ (х – 10)10 = 0.

223. Запишіть у вигляді степеня вираз:

1) 0,01 ∙ 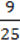СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ ∙ СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ ∙ 10;

2)0,125 ∙ СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ ∙ 0,5 ∙ 0,25;

3) 0,09 ∙ 0,09 ∙ 0,09 ∙ (-0,3) ∙ (-0,3) ∙ (-0,3);

4)4 ∙ 27 ∙ 9 ∙ 64 ∙ 3 ∙ 16;

5)-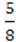СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ ∙ (-0,4) ∙ (-0,064) ∙ СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ.

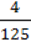224. За якого значення а вираз |-а|n для всіх натуральних значень n є:

1) додатним; 2) недодатним; 3) невід’ємним?

225. За якого значення a вираз (|-а| + a)n для всіх натуральних значень n дорівнює:

1) нулю; 2) одиниці?

226. Визначте знак виразу:

1) а3 ∙ (-а)4, якщо а < 0;

2) а2+ 32;

3) (-а)7 ∙ (-а)8, якщо а > 0.

227. Знайдіть значення виразу (а2 – 1) ∙ (а3 – 1) ∙ (а4 – 1 ) ∙ … ∙ (а100 – 1), якщо:

1) а = -1;

2) а = 1;

3) а = 0.

228. Знайдіть значення виразу (а2 – 1) ∙ (а2 – 2) ∙ (а2 – 3) ∙… ∙ (а2 – 100), якщо:

1) а = 8; 2) а = -6.

229. Спростіть вираз:

1) 11 + (-1)2 + 13 + (-1)4+…+119 + (-1)20;

2)(-1)1 + (-1)2 + …+(-1)20.

230. Знайдіть найменше значення виразу:

1)а2 – 4;

2) (а + 3)6 + 3;

3) |(-а)3| +98.

231. Розв’яжіть рівняння:

1) (36 – х) ∙ (43 – 82)=0;

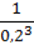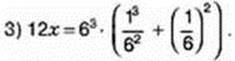
2) (2СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ)3 ∙ (25 – x) = СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ;

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

232. Розв’яжіть рівняння:

1) (3 – х)2 + (х – 2)6 = 0; 3) (2 – х)2 + |х – 2| = 0;

2) (100 + х)100 + (х + 102)10 = 0; 4) (5 – х)4 + (х + 5)4 = 0

233. Квадрат числа складається з цифр 6,5 і 2. Знайдіть це число.

234. Доведіть: 1) 1110 – 1 ділиться на 10; 2) 1010 + 5 ділиться на 3.

235. Доведіть: 1) 415 – 1 ділиться на 10; 2) 105 + 17 ділиться на 9.

236. Доведіть, що вираз – 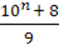СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ є натуральним числом для будь-якого натурального n.

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

237. Три кімнати мають форму квадратів зі сторонами відповідно а, b і с. Знайдіть суму площ чотирьох кімнат, якщо площа найбільшої з них дорівнює сумі площ трьох інших.

238. Дванадцяткова система числення була створена ще стародавніми шумерійцями (5 тис. до н. е.). Елементом такої системи нині може служити лічба дюжинами. Перший, другий і третій степені числа 12 мають власні назви: 1 дюжина = 12 штук, 1 грос = 12 дюжин, 1 маса = 12 гросів. Скільки штук: 1) в 1 масі; 2) в 1 гросі?

ЗАДАЧІ НА ПОВТОРЕННЯ

239. Знайдіть значення виразу:

1) |-280| + 15756 : 26 – 906;

2) 8585 : 101 – |-17| ∙ 5.

240. Обчисліть:

1) 4% числа 8, 25;

2) 15 % числа 5,24.

241. Пристань А розміщена нижче за течією річки від пристані В на 70 км. Швидкість човна у стоячій воді дорівнює 30 км/год, а швидкість течії річки – 5 км/год. Знайдіть час, за який човен подолає: 1) шлях від А до В; 2) шлях від В до А.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Степінь натурального числа з натуральним показником Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 7. Степінь натурального числа з натуральним показником Уже відомо, що суму, в якій всі доданки рівні між собою, можна записати коротше – у вигляді добутку. Наприклад, У математиці є спеціальний спосіб і для запису добутку, в якому всі множники рівні між собою. […]...

  2. Степінь з натуральним показником Математика – Алгебра Одночлени Степінь з натуральним показником Степенем Числа a з натуральним показником n, більшим за 1, називається добуток n множників, кожний із яких дорівнює a. Тобто де a – основа степеня; n – показник степеня. Степенем числа a з показником 1 є са­­ме число a. Знак степеня з натуральним показником 1. Якщо основа […]...

  3. Степінь з натуральним показником Урок № 20 Тема. Степінь з натуральним показником Мета: розширити знання учнів відомостями про властивості степенів раціональних чисел з парним та непарним показником; сформувати вміння застосовувати ці властивості під час розв’язування вправ. Тип уроку: застосування знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ № 1-2 – вправи на відтворення вмінь, набутих на […]...

  4. СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР ЗАДАЧІ НА ПОВТОРЕННЯ СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР 50. Обчисліть: 1)5 ∙ 26 + 22 – 4 ∙З4; 3) б2: 2 ∙ (43-55); 2) 2(2 ∙ 53- 102): 52; 4) 23: 12 ∙ 53-(32 ∙ 5-5). 51. Знайдіть значення виразу а3+ b2, якщо: 1) а = 2, b= 12; 2)а=1,b=1; […]...

  5. ПОВТОРЕННЯ. СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР Цілі: – навчальна: повторити поняття степеня натурального числа з натуральним показником; узагальнити знання учнів про площі та об’єми фігур; відтворити вміння розв’язувати задачі на обчислення площі прямокутника і квадрата, об’єму прямокутного паралелепіпеда і куба; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та систематизація […]...

  6. Властивості степеня з натуральним показником (продовження). Степінь степеня Урок № 23 Тема. Властивості степеня з натуральним показником (продовження). Степінь степеня Мета: свідоме засвоїти зміст властивостей піднесення степеня до степеня, виробляти вміння виконувати перетворення виразів із застосуванням раніше набутих знань про властивості степеня в комплексі з названою властивістю; систематизувати знання учнів про властивості степеня. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку I. […]...

  7. Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...

  8. Властивості степеня з натуральним показником Розділ 1. ЦІЛІ ВИРАЗИ & 4. Властивості степеня з натуральним показником Розглянемо властивості степеня з натуральним показником. Вираз а3а2 є добутком двох степенів з однаковими основами. Застосувавши означення степеня, цей добуток можна переписати так: А3а2 = (ааа) ∙ (аа) = ааааа = а5. Отже, а3а2 = а5, тобто a5 = а2 + 3. У той […]...

  9. Степінь з натуральним показником. Одночлени Урок № 29 Тема. Степінь з натуральним показником. Одночлени Мета: узагальнити та систематизувати знання та вміння учнів, набуті в ході вивчення названої теми, підготовити учнів до тематичного оцінювання. Обладнання: таблиця “Степінь. Властивість степеня”. Тип уроку: узагальнення та систематизація знань та вмінь. Хід уроку I. Перевірка домашнього завдання @ Цей етап уроку є ще аналізом самостійної […]...

  10. Степінь з натуральним показником та властивості степеня з натуральним показником Урок № 25 Тема. Степінь з натуральним показником та властивості Степеня з натуральним показником Мета: повторити, систематизувати та узагальнити знання учнів про означення та властивості степеня числа з натуральним показником; відпрацювати та вдосконалити вміння і навички щодо застосування названих теоретичних відомостей для спрощення виразів та виконання обчислень; здійснити проміжну діагностику засвоєних знань та вмінь у […]...

  11. Степінь числа Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 20. Степінь числа Як ви знаєте, за допомогою добутку зручно записувати суму кількох рівних доданків. Наприклад, 7+7+7 + 7 = 7∙4. У математиці придумали спосіб коротко записувати добуток, у якому всі множники рівні. Наприклад, 7 ∙ 7 ∙ 7 ∙ […]...

  12. ТИПИ СТЕПІНЬ ЧИСЛА РОЗДІЛ 4 СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР У розділі дізнаєтесь: Що таке степінь числа і як він пов’язаний із дією множення; Про дію піднесення до степеня та її властивості; Що таке квадрат і куб числа; Який порядок виконання дій у виразах, що містять степені; Що таке многокутник та які його […]...

  13. Степінь з натуральним показником. Одночлен Урок № 30 Тема. Степінь з натуральним показником. Одночлен Мета: діагностика рівня набутих знань та вмінь учнів з теми. Тип уроку: контроль знань, умінь, навичок. Хід уроку І. Умова тематичної контрольної роботи Варіант 1 Варіант 2 № 1. Знайдіть значення виразу: 1) 1,5 • 62 – 24; 2) 1) 2,5 • 25 – 72; 2) […]...

  14. Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь з раціональним показником N ) Для будь-якого невід’ємного числа а й натурального числа n (n ≥ 2) існує одне невід’ємне число b, при якому bn = а й позначається . Звідси випливає: 1. = 0 тільки при а = 0; 2. = 1 тільки при а = […]...

  15. ВЛАСТИВОСТІ СТЕПЕНЯ З НАТУРАЛЬНИМ ПОКАЗНИКОМ Цілі: – навчальна: удосконалити вміння застосовувати властивості степенів до розв’язування задач; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати об’єктивність та чесність під час оцінювання власних знань, старанність, наполегливість у досягненні мети; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ […]...

  16. Властивості степеня з натуральним показником. Добуток степенів з однаковою основою Урок № 21 Тема. Властивості степеня з натуральним показником. Добуток степенів з однаковою основою Мета: домогтися свідомого розуміння учнями властивості добутку степенів з однією основою та сформувати вміння перетворювати числові та буквені вирази з використанням цієї властивості. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання (Зібрати зошити) II. Актуалізація, опорних […]...

  17. Степінь з цілим від’ємним показником Тестові завдання Тестове завдання № 3 . Степінь з цілим від’ємним показником 1. При якому t правильна рівність ? А Б В Г -2 5 -5 -3 2. Знайдіть значення виразу . А Б В Г 1 3. Перетворіть у дріб: ху -1 + ху -2. А Б В Г 4. Обчисліть: 104 : (0,01) […]...

  18. Підсумковий урок з теми “Степінь з від’ємним цілим показником. Стандартний вигляд числа” Урок № 31 Тема. Підсумковий урок з теми “Степінь з від’ємним цілим показником. Стандартний вигляд числа” Мета: повторити, систематизувати та узагальнити знання і способи дій, які опанували учні під час вивчення теми “Степінь з цілим від’ємним показником. Стандартний вигляд числа”. Тип уроку: систематизація та узагальнення знань і вмінь. Наочність та обладнання: опорні конспекти. Хід уроку […]...

  19. Степінь Математика – Алгебра Подільність натуральних чисел Степінь Добуток n однакових множників, кожний із яких дорівнює а, називається n-м Степенем числа А і записується : , де n – натуральне число. Вираз називається степенем, число a – основою степеня, число n – показником сте­пеня. Приклади ; ....

  20. Властивості степеня з цілим від’ємним показником Урок № 26 Тема. Властивості степеня з цілим від’ємним показником Мета: закріпити знання учнів про означення та властивості степеня з цілим (від’ємним) показником та сформувати вміння використовувати їх для розв’язування вправ на обчислення значень числових виразів та перетворень виразів зі змінними. Тип уроку: відпрацювання навичок, діагностика засвоєння. Наочність та обладнання: опорний конспект “Степінь з цілим […]...

  21. Властивості степеня (продовження). Степінь добутку й відношення Урок № 24 Тема. Властивості степеня (продовження). Степінь добутку й відношення Мета: домогтися свідомого розуміння властивості степеня добутку й відношення; виробити вміння застосовувати ці властивості для перетворень виразів і обчислення значень числових виразів. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ Як і на попередніх двох уроках, перевірку домашнього […]...

  22. Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...

  23. Квадрат і куб від’ємного числа Урок № 8 4 Тема. Квадрат і куб від’ємного числа Мета: повторити поняття квадрата та куба числа (степінь з натуральним показником) та з’ясувати властивості квадрата і куба від’ємного числа; продовжити роботу на удосконалення умінь виконувати додавання та множення раціональних чисел із використанням їх властивостей. Тип уроку: застосування знань, вмінь, навичок. Хід уроку I. Перевірка домашнього […]...

  24. Означення степеня з цілим від’ємним показником Урок № 24 Тема. Означення степеня з цілим від’ємним показником Мета: домогтися засвоєння учнями змісту означення степеня з цілим від’ємним показником (для цілої та дробової основи степеня); сформувати вміння відтворювати означення степеня та застосовувати його для перетворення степеня з цілим від’ємним показником у дріб, та навпаки, сформувати вміння розв’язувати вправи на обчислення значень числових виразів […]...

  25. Многочлен. Подібні члени многочлена та їх зведення. Стандартний вигляд многочлена. Степінь многочлена Розділ 1. ЦІЛІ ВИРАЗИ & 7. Многочлен. Подібні члени многочлена та їх зведення. Стандартний вигляд многочлена. Степінь многочлена Вираз 7х2у3 – 5ху7 + 9х5 – 8 є сумою одночленів 7х2у3, -5ху7, 9×5 і -8. Цей вираз називають многочленом. Одночлени, з яких складається многочлен, називають членами многочлена. Наприклад, многочлен 7х2y – 5ху7 + 9х5 – 8 […]...

  26. СТАНДАРТНИЙ ВИГЛЯД МНОГОЧЛЕНА. СТЕПІНЬ МНОГОЧЛЕНА Цілі: – навчальна: сформувати поняття стандартного вигляду многочлена, степеня многочлена; сформувати вміння записувати многочлен у стандартному вигляді, знаходити степінь многочлена; – розвивальна: формувати вміння бачити закономірності; сприяти вдосконаленню обчислювальних навичок; – виховна: виховувати наполегливість у досягненні мети, почуття відповідальності; Тип уроку : засвоєння нових знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП […]...

  27. ДІЇ ЗІ СТЕПЕНЯМИ РОЗДІЛ II ОДНОЧЛЕНИ &6. ДІЇ ЗІ СТЕПЕНЯМИ Ви знаєте, що додавання і віднімання – це дії першого ступеня, множення і ділення – дії другого ступеня, а піднесення до степеня – дія третього ступеня. Зі степенями можна виконувати всі ці дії. Наприклад: 33 + 32 = 27 + 9 = 36, 33 – 32 = 27 […]...

  28. ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА ЗАДАЧІ НА ПОВТОРЕННЯ ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА 1. Скільки чисел натурального ряду розміщено між числами: 1)120 і 129; 2) 999 і 1100; 3)8901 і 8910; 4) 50000 і 50020? 2. На прямій дано три точки А, В і С. Знайдіть довжину відрізка ВС, якщо АВ = 8 см і АС – 9 см. Скільки розв’язків […]...

  29. Одночлен. Стандартний вигляд одночлена Розділ 1. ЦІЛІ ВИРАЗИ & 5. Одночлен. Стандартний вигляд одночлена Розглянемо вирази 7; – ; а9; – b; 7b2m; 4а2 ∙ (-5)ас. Це – числа, змінні, їх степені і добутки. Такі вирази називають одночленами. Вирази а + b2; с3 – 5m; 0,9а2 : m не є одночленами, оскільки містять дії додавання, віднімання, ділення. Спростимо одночлен […]...

  30. Узагальнення поняття степеня УРОК 40 Тема. Узагальнення поняття степеня Мета уроку. Формування поняття степеня з раціональним показником, степінь з ірраціональним показником. І. Перевірка домашнього завдання 1. Відповіді на запитання, що виникли в учнів при розв’язуванні домашнього завдання. 2. Колективне розв’язування нерівності < 4 – х. Відповідь: 0 < х < 2. II. Повторення і систематизація знань учнів про […]...

  31. Віднімання раціональних чисел. Властивості віднімання Урок № 7 4 Тема. Віднімання раціональних чисел. Властивості віднімання Мета: доповнити уявлення учнів властивостями віднімання; відпрацювати навички замінювати віднімання додаванням і знаходити значення утворених сум. Тип уроку: застосування знань, навичок та вмінь. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Закінчіть речення: “Щоб від числа [а] відняти число 7 [-6], […]...

  32. Корінь n-го степеня. Арифметичний корінь n-го степеня і його властивості УРОК 33 Тема. Корінь n – го степеня. Арифметичний корінь n – го степеня і його властивості Мета уроку. Повторити відомості про квадратний корінь. Формування понять корінь n-го степеня і арифметичний корінь n-го степеня. Вивчення властивостей коренів n-го степеня. І. Аналіз контрольної роботи з теми “Тригонометричні рівняння і нерівності” II. Повторення відомостей про квадратний корінь […]...

  33. Одночлен. Стандартний вигляд одночлена Урок № 26 Тема. Одночлен. Стандартний вигляд одночлена Мета: домогтися свідомого розуміння змісту основних понять уроку (одночлен; одночлен стандартного вигляду, коефіцієнт одночлена стандартного вигляду; степінь одночлена); вдосконалювати вміння виконувати перетворення степенів. Тип уроку: засвоєння знань учнів. Хід уроку I. Перевірка домашнього завдання @ Щоб перевірити корекцію самостійної роботи, збираємо зошити на перевірку та за необхідності […]...

  34. Многочлен та його стандартний вигляд Розв’яжіть задачі 372. 1) є многочленом; 2) є многочленом; 3) є многочленом; 4) є многочленом; 5) не є многочленом; 6) не є многочленом; 376. 1) 1) Ні; 2) ні; 3)так. 377. 1) у випадку 4). 378. Старший член многочлена – x5. 379. Вирази 2×2 – 2×3 та -3x – x3 записані у стандартному вигляді. 380. […]...

  35. МНОГОЧЛЕН ТА ЙОГО СТАНДАРТНИЙ ВИГЛЯД РОЗДІЛ 3 МНОГОЧЛЕНИ У розділі дізнаєтесь: ► що таке многочлен; ► який вигляд многочлена називають стандартним; ► що називають степенем многочлена; ► які властивості дій з многочленами; про формули скороченого множення; ► як розкладати многочлен на множники; ► як застосувати вивчений матеріал на практиці &8. МНОГОЧЛЕН ТА ЙОГО СТАНДАРТНИЙ ВИГЛЯД Запишемо суму одночленів х2, -15ху, […]...

  36. Степінь натурального числа. Розкладання натурального числа на прості множники Урок № 4 Тема. Степінь натурального числа. Розкладання натурального числа на прості множники Мета: повторити знання учнів про степінь натурального числа з натуральним показником, здобутих у 5 класі, і сформувати вміння використовувати алгоритм розкладання складених чисел на прості множники. Тип уроку: засвоєння нових знань. Хід уроку I. Перевірка домашнього завдання @ Оскільки програмою передбачений дуже […]...

  37. ПОВТОРЕННЯ. ДІЇ ДРУГОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ Цілі: – навчальна: повторити поняття множення та ділення натуральних чисел, закони множення; відтворити вміння виконувати множення та ділення натуральних чисел, розв’язувати задачі, які передбачають множення та ділення натуральних чисел; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та систематизація знань. Обладнання та наочність: Хід […]...

  38. Сполучна і розподільна властивості множення Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 17. Сполучна і розподільна властивості множення Нарисуємо на аркуші в клітинку прямокутник із сторонами 5 см і 3 см. Розіб’ємо його на квадрати зі стороною 1 см (рис. 142). Підрахуємо кількість клітинок зошита, що містяться в прямокутнику. Це можна зробити, […]...

  39. Перетворення виразів Уроки № 122, 123 Тема. Перетворення виразів 1. Спростіть вираз і знайдіть його значення при даних значеннях букв: а) -12b – 7b + 10b – b при b = -0,1; 2; -1; -5,7; 0; Б) -5а – 8а – 2а – 15a при а = -0,6; ; ; 0,002; -1; В) -4c + 9с – […]...

  40. Квадрат і куб числа Урок № 36 Тема. Квадрат і куб числа Мета уроку. Ознайомити учнів з новою дією – піднесення до степеня, позначенням і обчисленням а² і а3. Формувати вміння розв’язування вправ. Розвивати спостережливість, уважність. Хід уроку І. Робота в групах Ділене 246 521 837 245 Дільник 307 1208 63 217 Частка 651 837 245 1 ІІ. Сприймання […]...

Ви зараз читаєте: СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ
«
»