Степінь з натуральним показником та властивості степеня з натуральним показником
Урок № 25
Тема. Степінь з натуральним показником та властивості Степеня з натуральним показником
Мета: повторити, систематизувати та узагальнити знання учнів про означення та властивості степеня числа з натуральним показником; відпрацювати та вдосконалити вміння і навички щодо застосування названих теоретичних відомостей для спрощення виразів та виконання обчислень; здійснити проміжну діагностику засвоєних знань та вмінь у ході самостійної роботи.
Тип уроку: систематизація та узагальнення знань.
Хід уроку
I. Перевірка
@ Оскільки вправи № 1-2 є вправами на закріплення знань та способів дій, розглянутих на попередньому уроці, перевірку або здійснюємо усно, або перед уроком перевіряємо їх тільки в слабких учнів (або за умови налагодженої систематичної роботи учнів-консультантів перевірку домашнього завдання доручаємо їм).
II. Робота з випереджальним домашнім завданням
1. Самостійна робота учнів. Учні, спираючись на виконаний № 3 у домашньому завданні, заповнюють таблицю:
Арифметична дія зі степенем | Запис алгоритму у вигляді рівності | Корекція |
Дія | Запис | |
1. 2. 3. |
2.
III. Систематизація та узагальнення знань
@ Після виконання роботи з випереджальним домашнім завданням учні повинні усвідомити, що:
1) оскільки степінь – це короткий запис добутку однакових множників, то зі степенями виконують такі дії: множення (степенів з однаковою основою та однаковим показником – зводиться до дій із показниками або основами); ділення (обернена дія до множення) та піднесення до степеня (як особливий випадок степеня);
2) властивості степеня (див. попередні уроки) допомагають: по-перше, спрощувати буквені вирази, не обчислюючи значень степенів, та, по-друге, знаходити значення числових виразів, що складаються зі степенів, не виконуючи складних обчислень.
Тобто, використовуючи властивості степеня, ми замінюємо поданий вираз на тотожно рівний йому вираз, але в новому виразі порядок виконання дій змінився (і замість того щоб виконувати піднесення до степеня, ми виконуємо або додавання / віднімання показників, або множення / ділення основ степенів).
Бажано, щоб робота із систематизації та узагальнення знань з теми супроводжувалась наочністю, наприклад відповідного змісту таблицею (або учні складають її самотужки).
Таблиця 1 | |
Степінь з натуральним показником | |
1. Означення | |
2. Властивості: 1) 1n = 1; 0n = 0; a1 = а; a0 = 1 (а? 0) | 5) (am)n = amn |
2) (-а)2m = а2m; (-а)2m – 1 = – а2m – 1 | 6) (ab)m = ambm |
3) аm – an = аm+n | 7) |
4) |
|
IV. Застосування знань, умінь та навичок
Виконання письмових вправ
1. Обчисліть значення виразу:
1) 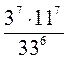 ; 2)
; 2) 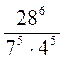 ; 3)
; 3) 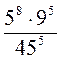 ; 4)
; 4) 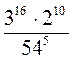 ; 5)
; 5) 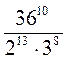 ; 6)
; 6) 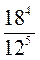 .
.
@ Щоб спонукати учнів до самостійних свідомих дій під час виконання завдання, можна запропонувати їм попрацювати за алгоритмом:
1. Усвідом, як ти зрозумів завдання.
2. Сформулюй питання, на які треба відповісти.
3. Систематизуй, в якій послідовності їх треба висвітлити. Постав собі запитання: “Чому саме так?” – і спробуй на нього відповісти.
4. Знайди шляхи отримання відповіді на ці запитання (підручник, конспект, запитання вчителю, товаришу і т. ін.).
5. Зроби висновок: яких нових знань набув, що є головним, яка ідея приваблива, про що йде мова і т. ін.
@ Якщо така робота з яких-небудь причин неможлива, учитель за цим самим алгоритмом розкриває хід своїх думок під час виконання подібного завдання, тобто формулює своєрідний загальний алгоритм виконання завдання та обчислення значення виразу, що с відношенням двох виразів – добутків степенів. (Важливо, щоб уші усвідомили, що без застосування властивостей степеня обчислення будуть украй складними.)
V. Діагностика засвоєння знань та вмінь
Самостійна робота
@ Щоб врахувати важливі відмінності в рівні підготовки учнів, пропонуємо самостійну роботу трьох рівнів складності.
І рівень
Варіант 1 | Варіант 2 |
1. Виконайте дії: | |
1) 3 – 52 – 23; 2) -70 + (-1)5. | 1) 72 – 2 – 33; 2) (-1)7 – 30. |
2. Спростіть вираз: | |
1) с5 – с7 : с8; 2) (с4)3 – с; 3) (-3с)4; 4) ((с2)3)4. | L) а19 : а13; 2) (а5)2 : а; 3) (-5а)2; 4) ((а4)3)5. |
3. Обчисліть, використовуючи властивості степеня: | |
1) 213 – 0,513; 2) | 1) 0,2510 – 410; 2) |
II рівень
Варіант 1 | Варіант 2 |
1. Виконайте дії: | |
1) 0,2 – (-4)2 – 8 – | 1) 27 – |
2. Спростіть вираз: | |
1) (с3)4 – с5; 2) | 1) (а4)5 – а4; 2) |
3. Обчисліть, використовуючи властивості степеня: | |
1) 0,045 – 255; 2) | 1) 12,510 – 0,810; 2) |
III рівень
Варіант 1 | Варіант 2 |
1. Обчисліть: | |
1) | 1) |
2. Спростіть вираз: | |
1) | 1) |
3. Обчисліть, використовуючи властивості степеня: | |
1) | 1) |
VI. Рефлексія
– Які завдання були незрозумілі?
– Які завдання викликають сумнів?
VII. Домашнє завдання
№ 1. Задається індивідуально: після здійснення рефлексії учні самі вибирають ті вправи самостійної роботи, які викликали труднощі під час її виконання. Для заохочення учнів до роботи можна наступного уроку зібрати зошити й оцінити виконання вправ. За умови успішного виконання можна вважати це домашнє завдання корекцією самостійної роботи й підвищити оцінку в журналі.
№ 2. Випереджальне домашнє завдання. (Робота з текстом підручника за алгоритмом свідомого сприйняття тексту.)
Знайдіть у тексті підручника пункт “Одночлен” і виконайте таке завдання:
1) виділіть незрозумілі слова, поняття, терміни та зайдіть їх означення в підручнику або довіднику (тлумачному словнику);
2) виділіть ключові слова, тобто слова, що розкривають основний зміст пункту;
3) наведіть власні смислові порівняння виділених слів, термінів.
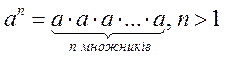
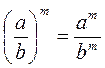 (b? 0)
(b? 0)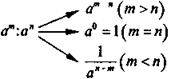
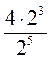 .
.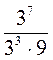 .
.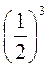 ; 2) (-0,4)3 – 0,40.
; 2) (-0,4)3 – 0,40.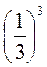 – 0,03 – (-10)2; 2) (-0,7)0 – 0,72.
– 0,03 – (-10)2; 2) (-0,7)0 – 0,72.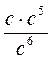 ; 3) (-2cd)3; 4) ((-с5)2)4.
; 3) (-2cd)3; 4) ((-с5)2)4.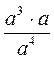 ; 3) (-3аb)3; 4) (((-a)3)2)5.
; 3) (-3аb)3; 4) (((-a)3)2)5.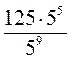 .
.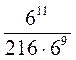 .
.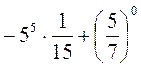 ; 2)
; 2) 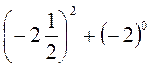 .
.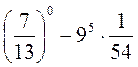 ; 2)
; 2) 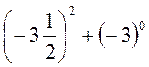 .
.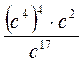 ; 2)
; 2) 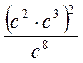 ; 3) (-3c3d2e)3; 4) (cn+5)2 : ((-c2)3)2.
; 3) (-3c3d2e)3; 4) (cn+5)2 : ((-c2)3)2.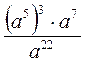 ; 2)
; 2) 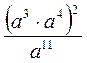 ; 3) (-5а3bс2)3; 4) (аn-3)5 • ((-a4)2)5.
; 3) (-5а3bс2)3; 4) (аn-3)5 • ((-a4)2)5.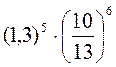 ; 2)
; 2) 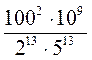 .
.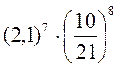 ; 2)
; 2) 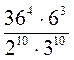 .
.