Теорема, обернена до теореми Піфагора
Урок № 35
Тема. Теорема, обернена до теореми Піфагора
Мета: домогтися свідомого розуміння учнями змісту теореми Піфагора та її доведення: сформувати поняття єгипетського трикутника, піфагорової трійки чисел, піфагорових трикутників. Формувати вміння відтворювати зміст вивченої теореми та застосовувати її під час розв’язування задач на доведення.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект “Теорема Піфагора”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Засвоєння
Математичний диктант
Варіант 1 | Варіант 2 | |
1 | Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють відповідно 5 м і 12 м | Знайдіть катет прямокутного трикутника, якщо його інший катет і гіпотенуза дорівнюють відповідно 40 см і 41 см |
2 | Запишіть теорему Піфагора для? АВС, у якому | |
|
| |
3 | Знайдіть | Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють відповідно 6 мм і 8 мм |
4 | Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює 6,5 см. Знайдіть трикутники, якщо один із катетів має довжину 5 см | Знайдіть радіус кола, описаного навколо прямокутного трикутника з катетами 8 дм і 15 дм |
Розв’язання письмових вправ перевіряємо під час усної роботи за готовими рисунками до цих задач.
III. Формулювання мети і завдань уроку
Створити позитивну мотивацію пізнавальної діяльності учнів можна, провівши цей етап уроку в ігровій формі.
Гра “Що? Де? Коли?”
Питання знавцям
Давні єгиптяни будували прямі кути на місцевості таким чином: ділили вузлами мотузку на 12 рівних частин, зв’язували її кінці, після чого мотузку розтягувати на землі так, щоб утворився трикутник зі сторонами 3, 4 і 5 поділок. Кут трикутника, що лежав проти сторони з 5-ма поділками, був прямий. Чи можете ви обгрунтувати правильність цієї побудови або спростувати її?
У результаті пошуку відповідей па запитання учні мають зрозуміти, що з математичної точки зору питання ставиться як визначення того, чи буде трикутник зі сторонами 3, 4, 5 одиниць прямокутним. Також учні мають зрозуміти, що застосування теореми Піфагора для розв’язування задачі неможливе (бо в умові немає твердження, що трикутник є прямокутним).
Таким чином формулюється загальна проблема: як, не проводячи вимірювань, визначити, чи с трикутник із заданими довжинами (співвідношенням) сторін прямокутним, – розв’язання якої і є основною метою уроку.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями змісту теореми, оберненої до теореми Піфагора, та її доведення учням слід активізувати знання і вміння щодо означення прямокутного трикутника; ознак рівності трикутників; теореми Піфагора.
Виконання усних вправ
1. Дано:  M =
M =  B = 90°, МС = ВС (рис. 1). Доведіть, що АВ = МН.
B = 90°, МС = ВС (рис. 1). Доведіть, що АВ = МН.
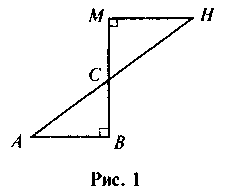
2. Дано: AB 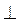 AD, CD
AD, CD 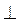 AD,
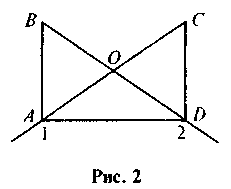
AD, 1 =
1 =  2 (рис.2).Доведіть, що? ABD = ?DCA.
2 (рис.2).Доведіть, що? ABD = ?DCA.
3. Диктант.
1) Якщо катети прямокутного трикутника дорівнюють 12 см і 9 см, то гіпотенуза дорівнює…
2) Якщо дві більші сторони прямокутного трикутника дорівнюють 17 і 15, то третя сторона дорівнює…
3) Якщо діагональ квадрата дорівнює 12 см, то сторона квадрата має довжину…
4) Якщо діагоналі ромба мають довжини 12 см і 16 см, то сторона ромба має довжину.
V. Засвоєння знань
План вивчення нового матеріалу
1. Теорема, обернена до теореми Піфагора: формулювання та доведення.
2. Єгипетський трикутник.
3. Піфагорові трійки чисел, піфагорові трикутники.
@ Матеріал, винесений для вивчення на урок, донедавна містився у підручнику у вигляді опорної задачі. За новою програмою з математики серед програмових вимог знання теореми, оберненої до теореми Піфагора, та вміння доводити її, також окремо не виділені. Проте розв’язування багатьох задачі, пов’язаних із прямокутним трикутником, базується саме на застосуванні цієї теореми. Тому, вивчивши теорему Піфагора, учні мають принаймні ознайомитися із змістом та доведенням оберненої теореми, а також сформувати вміння застосовувати її для визначення виду трикутника із заданими довжинами сторін.
Зміст матеріалу п. і 3.2, що міститься після доведення теореми, не є обов’язковим для вивчення всіма учнями, проте, з огляду на те, що в задачах досить часто фігурують саме піфагорові трикутники, знання цього поняття, а також знання учнями декількох піфагорових трійок (найбільш часто зустрічаються трійки: 3, 4, 5; 5, 12, 13; 6, 8, 10; 8, 15, 17) може допомогти учням суттєво спростити обчислення невідомих сторін трикутників. (Для учнів, які цікавляться математикою, пропонуються формули для складання піфагорових трійок.)
Якщо m і n – натуральні числа, то числа 2mn, m2 – n2 і m2 + n2 складають піфагорові трійки. Доведіть.
VI. Формування первинних умінь
З метою закріплення знань учнів щодо змісту теореми, оберненої до теореми Піфагора, а також формування вмінь застосування твердження цієї теореми до розв’язування задач, учні мають послідовно розв’язати усні задачі.
Виконання усних вправ
1. Чи правильно визначено вид трикутника?
А) Оскільки 122 ? 132 + 52, то трикутник зі сторонами 5, 12, 13 не є прямокутним;
Б) оскільки 6 = 5 + 1, то сторона довжиною 6 одиниць лежить проти прямого кута.
2. Визначте вид трикутника ABC, якщо:
1) АС = 5, ВС = 6, АС = 7;
2) АС = 4, BC = 2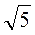 , AC = 6.
, AC = 6.
3. Яку градусну міру має найбільший кут трикутника зі сторонами 6, 8 і 10? Чому?
4. Сторони паралелограма дорівнюють 3 см і 4 см, а діагональ – 5 см. Визначте вид паралелограма.
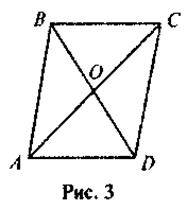
5. Чи правильно зроблено до рисунка 3 такий запис: “Дано АВ = 5 см, BD = 4 см, АС = 6 см, ABCD – паралелограм”?
Виконання графічних вправ
Побудуйте трикутник зі сторонами 2,5 см, 6 см і 6,5 см. Виміряйте найбільший кут трикутника. Підтвердьте здобутий результат за Допомогою теореми, оберненої до теореми Піфагора.
Виконання письмових вправ
1. Визначте, чи є прямокутним трикутник зі сторонами:
А) 4, 5, 6;
Б) 2, 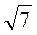 ,
, 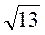 .
.
2. Діагоналі паралелограма дорівнюють 16 см і 30 см, а сторона – 17 см. Доведіть, що даний паралелограм є ромбом.
3. Сторони трикутника дорівнюють 15 см, 20 см і 25 см. Знайдіть медіану і висоту, проведену до найбільшої сторони.
4. Знайдіть висоти трикутника, якщо його сторони дорівнюють 7 см, 24 см і 25 см.
Крім того, на уроці слід виділити час для розв’язування задач на застосування теореми Піфагора.
Виконання письмових вправ
1. У рівнобедреному прямокутному трикутнику знайдіть:
А) гіпотенузу, якщо катет дорівнює 4 см; 2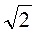 см; а см;
см; а см;
Б) катет, якщо гіпотенуза дорівнює 10 см; 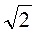 см; с см.
см; с см.
2. Дві сторони прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть довжину третьої сторони. Скільки розв’язків має задача?
3. У рівносторонньому трикутнику знайдіть висоту, якщо сторона дорівнює 6 см; 2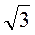 см; а см.
см; а см.
4. Висота рівнобедреного трикутника ділить бічну сторону на відрізки завдовжки 1 см і 12 см, починаючи від основи. Знайдіть основу трикутника.
@ Під час розв’язування залам на пряме застосування теореми, оберненої до теореми Піфагора (див. усні вправи № 2, 3), слід вимагати від учнів попереднього відтворення змісту теореми із наступним записом відповідної рівності і перевіркою правильності здобутої рівності.
Також на уроці продовжується формування вмінь застосовувати теорему Піфагора. Тому, щоб уникнути плутанини, слід зауважити учням, що вивчені теореми мають різні сфери застосування: теорема Піфагора застосовується у випадку, коли за умовою задачі дано прямокутний трикутник (або існування прямокутного трикутника обумовлено властивостями фігур, даних в умові – див. властивості чотирикутників та поняття висоти трикутника); обернена теорема використовується у випадку, коли умова задачі містить довжини сторін деякого трикутника (абсолютні значення або у вигляді виразів чи відношень) і умовою задачі вимагається визначити, чи є трикутник прямокутним.
Також слід звернути увагу на задачі №1,3 (письмові вправи) – у задачах виводяться формули, які корисно зафіксувати в конспектах учнів як опорні.
Гіпотенуза прямокутного рівнобедреного трикутника з катетом а обчислюється за формулою с = а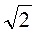 ; висота рівностороннього трикутника зі стороною а обчислюється за формулою
; висота рівностороннього трикутника зі стороною а обчислюється за формулою 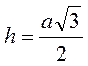 .
.
VII. Підсумки уроку
Дві сторони трикутника мають довжини 4 см і 5 см. Якою може бути довжина третьої сторони, щоб цей трикутник був прямокутним? Піфагоровим?
VIII. Домашнє завдання
Вивчити зміст основних понять уроку.
Розв’язати задачі.
1. У квадраті знайдіть:
А) діагональ, якщо сторона дорівнює а;
Б) сторону, якщо діагональ дорівнює d.
2. Сторони трикутника дорівнюють 12 см, 16 см і 20 см. Який кут утворює з найменшою стороною бісектриса найбільшого кута?
3. У рівносторонньому трикутнику знайдіть сторону, якщо висота дорівнює 1 см; 3 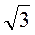 см: h см.
см: h см.
Повторити означення перпендикуляра до прямої, теорему Піфагора, властивості сторін прямокутного трикутника.