ТЕОРЕМИ І АКСІОМИ
РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ
& 8. ТЕОРЕМИ І АКСІОМИ
Ви вже маєте уявлення про теореми. Теорема – це твердження, в істинності якого переконуються за допомогою логічних міркувань, доведень.
Звичайно теорема містить умову (те, що дано) і висновок (що вимагається довести). Щоб виокремити умову і висновок теореми, її зручно подати у формі “Якщо…, то…”. Наприклад:
“Якщо кути вертикальні, то вони рівні”. Тут слова перед комою виражають умову теореми, а після коми – висновок.
Часто умову теореми
Наприклад, теорему про вертикальні кути (мал. 108) можна оформити так.
Дано: ∠AOD, ∠ВОС – вертикальні кути.
Довести: ∠AOD = ∠ВОС.
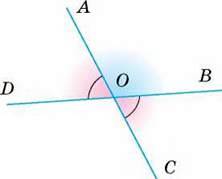
Мал. 108
Доведення.
∠AОВ = 180° – ∠AОВ (∠AОВ і ∠AОВ – суміжні),
∠BOC = 180° – ∠AOB (∠BOC і ∠AОВ – суміжні).
Отже, ∠AОВ = ∠ВОС.
Помінявши умову і висновок теореми місцями, одержимо нове твердження (істинне або хибне). Якщо одержане таким способом твердження істинне, його називають теоремою, оберненою до даної. Наведемо приклад.
1. “Якщо
2. “Якщо відповідні кути рівні, то прямі – паралельні” – дана теорема. “Якщо прямі паралельні, то відповідні кути – рівні” – теорема, обернена до даної.
Найважливіші теореми, у яких подано критерії чого-небудь, називають ознаками.
Доводячи теорему, показують, що вона випливає з інших істинних тверджень. Однак на початку вивчення геометрії ще ніяких “інших істинних тверджень” немає. Тому кілька перших тверджень зазвичай приймають без доведень. Їх називають аксіомами.
Деякі аксіоми вам уже відомі. Сформулюємо їх ще раз.
– Яка б не була пряма, існують точки, що належать цій прямій, і точки, що їй не належать.
– Через будь-які дві різні точки можна провести пряму, і тільки одну.
– Із трьох точок прямої одна, і тільки одна, лежить між двома іншими.
– Кожний відрізок має певну довжину.
– Кожний кут має певну міру.
– Через точку, що не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній.
Від теорем і аксіом слід відрізняти означення, у яких розкривається зміст поняття. Наприклад: “Відрізком називається частина прямої, обмежена двома її точками” – означення відрізка; “Гострим кутом називається кут, менший від прямого” – означення гострого кута.
В означеннях, аксіомах і теоремах – основний зміст геометрії, їх треба знати, але формулювати (правильно!) можна і своїми словами. Наприклад, означення відрізка можна формулювати й так: “Відрізок – це частина прямої, обмежена двома її точками” або так: “Частину прямої, обмежену двома її точками, називають відрізком”.
Для допитливих
1. Слово аксіома – грецького походження. Спочатку це слово означало: повага, авторитет, незаперечність. Згодом словом “аксіома” стали називати твердження, яке приймається без обгрунтування.
2. Слово теорема також грецького походження. Спочатку теоремою називали видовище, театральну виставу. Першим геометрам доведені ними теореми здавалися досить несподіваними, дивними, мов цікаві видовища. І справді дивно: з небагатьох примітивних тверджень, які приймаються без доведень, шляхом самих міркувань, людина може отримати мільйони неочевидних наслідків. Навіть таких, які в природі не можна спостерігати. І таких, про існування яких не здогадувався жоден мислитель.
3. Щоб і ви зрозуміли, яке задоволення відчували перші геометри, відкриваючи і доводячи все нові й нові властивості геометричних фігур за допомогою самих лише міркувань, спробуйте відповісти на одне з таких запитань.
Подивіться на малюнок 109. На ньому виділено 6 точок: середини сторін трикутника ABC і основи його висот. Здається, усі ці точки лежать на одному колі. Чи справді це так?
Чи в кожному трикутнику? Хто першим виявляв подібні закономірності й обгрунтовував їх, той відчував велике задоволення, немов мандрівник, який першим прийшов туди, де жодна інша людина ще не бувала, або спортсмен, який побив світовий рекорд.
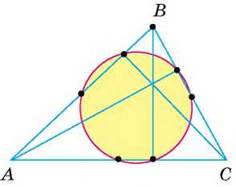
Мал. 109
Запитання і завдання для самоконтролю
1. Що таке теорема? Наведіть приклади теорем.
2. Що таке аксіома? Наведіть приклади аксіом.
3. Що таке означення? Наведіть приклади означень.
4. Яке твердження називають теоремою, оберненою до даної?
5. Що таке ознака?
Виконаємо разом
1. Бісектриси внутрішніх різносторонніх кутів, утворених січною з двома паралельними прямими, паралельні одна одній. Доведіть. Сформулюйте обернене твердження.
– Нехай ВС – січна прямих АВ і CD, кути ABC і BCD – внутрішні різносторонні, а ВК і СР – їх бісектриси (мал. 110). Покажемо, що коли АВ ‖ CD, то ВК ‖ СР.
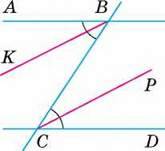
Мал. 110
Якщо АВ ‖CD, то ∠ABC = ∠BCD (як внутрішні різносторонні при паралельних прямих). Половини рівних кутів – рівні, тому ∠KBC = ∠ВСР. Ці кути – внутрішні різносторонні для прямих КВ і СР та січної ВС. Оскільки ці кути рівні, то прямі КВ і СР – паралельні.
А це й треба було довести.
Обернене твердження: якщо бісектриси внутрішніх різносторонніх кутів, утворених двома прямими з їх січною, – паралельні, то паралельні й дані прямі.
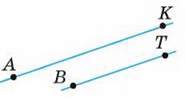
2. Два промені називають співнапрямленими, якщо один із них є частиною другого або якщо вони паралельні й розміщені по один бік від прямої, що проходить через їх початки. Наведіть приклади.
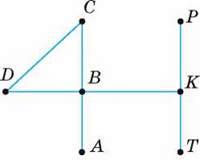
– Наприклад, промені АК і ВК (мал. 111), а також промені АК і ВТ (мал. 112).
3. Доведіть, що кути із співнапрямленими сторонами рівні.
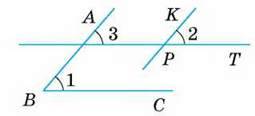
– Доведемо, що коли промені ВА і РК, ВС і РТ – співнапрямлені, то кути 1 і 2 – рівні.
Якщо дані кути розміщені, як показано на малюнку 113, то ∠1 = ∠3 і ∠3 = ∠2. Отже, ∠1 = ∠2.
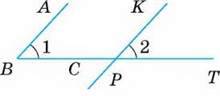
Якщо дані кути розміщені, як показано на малюнку 114, то промінь РТ становить частину променя ВС. У цьому випадку ∠1 = Z 2 як відповідні кути при паралельних прямих ВА і РК.
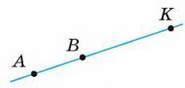
Мал. 111
Мал. 112
Мал. 113
Мал. 114
ЗАДАЧІ І ВПРАВИ
Виконайте усно
225. Сформулюйте означення:
А) вертикальних кутів; б) суміжних кутів.
226. Сформулюйте аксіоми про розміщення точок на прямій.
227. Сформулюйте аксіоми про вимірювання відрізків.
228. Сформулюйте аксіому Евкліда про паралельність прямих.
229. Чи через кожні три точки можна провести пряму? Чи існують три точки, через які можна провести пряму?
230. Чи існують 4 точки, через які можна провести пряму?
231. Сформулюйте ознаку подільності натуральних чисел на 3. Як її можна сформулювати інакше?
232. Яке з тверджень правильне:
А) “Якщо кожне з двох натуральних чисел ділиться на 10, то і їх сума ділиться на 10”;
Б) “Якщо сума двох натуральних чисел ділиться на 10, то кожне з них ділиться на 10”?
А
233. Сформулюйте теорему про суміжні кути. Подайте її у формі” Якщо…, то…”. Зазначте її умову і висновок.
234. Сформулюйте теорему про дві прямі, паралельні третій. Запишіть її за допомогою математичних символів.
235. Які з даних тверджень – істинні:
А) “Якщо кути рівні, то вони вертикальні”;
Б) “Якщо кути не вертикальні, то вони не рівні”;
В) “Якщо кути не рівні, то вони не вертикальні”?
236. Сформулюйте твердження, обернене до теореми 1. Чи можна вважати його теоремою? Чому?
237. Сформулюйте твердження, обернене до теореми 5. Чи є воно теоремою?
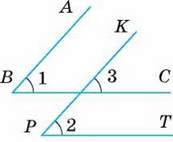
238. Дивлячись на малюнок 115, учень міркує: “Якщо АВ ‖ КР і ВС ‖ РТ, то ∠1 = ∠3 = ∠2.
Отже, кути з відповідно паралельними сторонами – рівні”. Чи правильно він міркує? Розгляньте інші можливі випадки.
Мал. 115
239. Чи можна вважати правильними такі означення:
А) “Бісектрисою кута називають пряму, яка ділить цей кут навпіл”;
Б) “Бісектрисою кута називають промінь, який ділить цей кут на рівні частини”?
240. Прочитайте три перші абзаци & 3 “Кути і їх міри”. Чи є в них означення? Сформулюйте одне з них.
Б
241. Сформулюйте означення паралельних прямих. Чи можна слова “на площині” опустити? Чому?
242. Яке з тверджень правильне:
А) ” Якщо кожне з трьох натуральних чисел ділиться на 5, то їх сума також ділиться на 5″;
Б) “Якщо сума трьох натуральних чисел ділиться на 5, то кожне з них ділиться на 5 ” ?
243. Доведіть, що кут між бісектрисами двох вертикальних кутів – розгорнутий. Сформулюйте і доведіть аналогічне твердження про бісектриси двох суміжних кутів.
244. Сформулюйте словами і доведіть твердження:
А) якщо а ‖ b і b ‖ с, то а ‖ с;
Б) якщо а ⏊ b і b ⏊ с, то а ‖ с.
Чи правильні ці твердження, якщо прямі а, b і с не лежать в одній площині?
245. Доведіть, що:
А) якщо кут А дорівнює куту В, а кут В дорівнює куту С, то кути А і С дорівнюють один одному;
Б) якщо відрізок АВ дорівнює відрізку КР, а КР дорівнює відрізку МТ, то відрізок АВ дорівнює відрізку МТ.
246. Чи правильні твердження:
А) “Якщо кут А суміжний з кутом В, а кут В суміжний з кутом С, то кути А і С – суміжні”;
Б) “Якщо кут А вертикальний з кутом В, а кут В вертикальний з кутом С, то кути А і С – також вертикальні”;
В) ” Якщо прямі а і с лежать в одній площині і прямі с і n лежать в одній площині, то прямі а і n також лежать в одній площині”?
247. Паралельні залізничні рейки, промені сонця та багато інших моделей прямих на фотографіях і картинах часто зображають у вигляді непаралельних прямих (мал. 116). Наведіть приклади зображень, на яких непаралельні прямі мають вигляд паралельних.
248. Доведіть, що січна, перетинаючи паралельні прямі, утворює з ними:
А) рівні зовнішні різносторонні кути;
Б) зовнішні односторонні кути, які в сумі становлять 180°.
249. Доведіть, що кути з відповідно перпендикулярними сторонами рівні або в сумі становлять 180°.

Мал. 116
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
250. Скільки існує на прямій точок, які лежать між даними її точками А і В?
251. На які частини пряму ділять дві її точки?
252. Скільки різних відрізків зображено на малюнку 117? Назвіть їх.
253. Скількома різними ламаними можна сполучити дві дані точки К і Р? А скількома відрізками? Скількома дугами кіл?
254. Дюйм – це 2,5 см. Скільки квадратних сантиметрів має квадратний дюйм?
Мал. 117
Геометрія навколо нас

ЗАДАЧІ ЗА ГОТОВИМИ МАЛЮНКАМИ
А
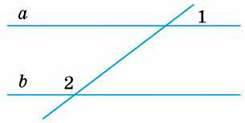
1
∠1 = 50°, ∠2 = 130°.
Довести: а ‖ b.
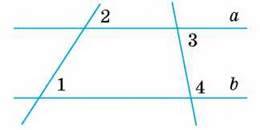
2
∠1 = ∠2, ∠3 = 80°.
∠4.
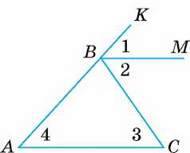
3
∠2 = ∠3.
Довести: ∠1 = ∠4
4
А ‖ b, ∠1 = 60°.
∠2
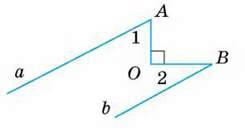
Б
1
∠1 : ∠2 = 3: 2, ∠3 = 72.
Довести: а ‖ b.
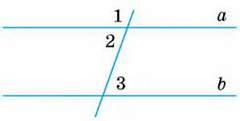
2
∠3 + ∠4 = 180°.
Довести: ∠1 = ∠2.
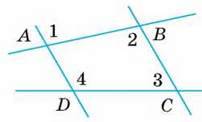
3
А ‖ b, ∠1 = ∠2.
Довести: с ‖ d
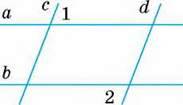
4
А ‖ b.
∠C
Самостійна робота |
Варіант 1
1. Відрізки АВ і КР перетинаються у внутрішній точці О так, що ∠AOK = 50°. Знайдіть міри кутів АОР, ВОР і ВОК.
2. Один із двох суміжних кутів більший за інший на 18°. Знайдіть ці кути.
З. Через кінці відрізка АВ з одного боку від прямої АВ проведіть промені АК і ВС так, щоб ∠КАВ = 107°, а ∠АВС = 73°. Чи паралельні ці промені? Чому?
Варіант 2
1. Відрізки MN і КТ перетинаються у внутрішній точці X так, що АМХК = 65°. Знайдіть міри кутів МХТ, TXN і KXN.
2. Знайдіть міри двох суміжних кутів, якщо один із них утричі більший за інший.
З. Через кінці відрізка АВ з одного боку від прямої АВ проведіть промені AM і ВС так, щоб ∠МАВ = 102°, а ∠АВС = 77°. Чи паралельні ці промені? Чому?
Варіант З
1. Відрізки АС і МР перетинаються у внутрішній точці О так, що ∠МОС = 48°. Знайдіть міри кутів АОР, АОМ і РОС.
2. Знайдіть міри двох суміжних кутів, якщо один із них на 26° більший за інший.
З. Через кінці відрізка КР з одного боку від прямої КР проведіть промені КА і РВ так, щоб ∠АКР = 97°, а ∠КРВ = 83°. Чи паралельні ці промені? Чому?
Варіант 4
1. Відрізки АВ і CD перетинаються у внутрішній точці М так, що ∠АМС = 35°. Знайдіть міри кутів AMD, CM В і BMD.
2. Знайдіть міри двох суміжних кутів, якщо один із них на 15° менший від іншого.
З. Через кінці відрізка АВ з одного боку від прямої АВ проведіть промені АК і ВМ так, щоб ∠КАВ = 58°, а ∠АВМ =123°. Чи паралельні ці промені? Чому?
Тестові завдання 2
1. Яку міру має кут, суміжний із кутом 100°? | А) 100°; б) 80°; В) 8°; г) 50°. |
2. Яким є кут, суміжний із тупим кутом? | А) тупим; Б) прямим; В) гострим; Г) розгорнутим. |
3. ∠АОР і ∠ВОС – вертикальні кути. Який знак слід поставити замість * в записі: ∠АОР * ∠ВОС? | А) <; б) =; В) >; г)>. |
4. Сума трьох кутів, утворених при перетині двох прямих, дорівнює 280° Знайдіть міру четвертого кута. | А) 100°; б) 80°; В) 90°; г) 70°. |
Для виконання завдань 5-10 скористайтеся малюнком 118. | |
5. Який знак слід поставити замість * в записі: СВ * ∠P? | А) ‖; Б) =; В) ∈; Г) ⏊. |

ТИПОВІ ЗАДАЧІ ДЛЯ КОНТРОЛЬНОЇ РОБОТИ
1. Точки А, В і С лежать на одній прямій, АВ = 7,3 см, ВС = 3,7 см.
Знайдіть довжину відрізка АС. Розгляньте два випадки.
2. Внутрішній промінь ОК кута АОВ розбиває його на кути АОК і КОВ. Знайдіть міру кута:
А) АОВ, якщо ∠AOK = 30°, ∠KOB = 40°;
Б) КОВ, якщо ∠АОВ = 79°, ∠KOA = 53°;
В) КОА, якщо він на 20° менший від кута КОВ і ∠АОВ = 80°.
3. Накреcліть ∠ABC = 120°. Проведіть його бісектрису ВМ і бісектрису ВК кута МВС. Знайдіть міри кутів КВС і АВК.
4. Знайдіть міри чотирьох кутів, утворених при перетині двох прямих, якщо один із них дорівнює 45°.
5. Знайдіть міри суміжних кутів, якщо один із них:
А) на 25° більший за інший;
Б) у 3 рази менший від іншого.
6. За допомогою малюнка 119 установіть:
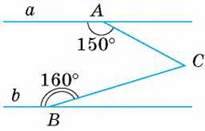
А) чи паралельні прямі АВ і CD;
Б) міру кута КРМ.
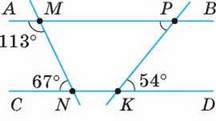
Мал. 119
7. Дві паралельні прямі перетинає третя пряма так, що сума двох із восьми утворених кутів дорівнює 240°. Знайдіть міри всіх утворених кутів.
8. Відрізки АВ і КР перетинаються в точці О. Доведіть, що якщо ∠AKO = ∠ОРВ, то ∠KAO = ∠OBP.
9. Прямі АВ і КР перетинаються в точці О. ОМ – бісектриса кута АОР. Знайдіть міру кута КОМ, якщо ∠АОК – ∠АОМ = 36°.
10. Доведіть, що бісектриси внутрішніх односторонніх кутів при паралельних прямих – перпендикулярні.
Запитання і завдання для самоконтролю
1. Які кути називають суміжними?
2. Сформулюйте і доведіть властивість суміжних кутів.
3. Які кути називають вертикальними?
4. Сформулюйте і доведіть властивість вертикальних кутів.
5. Що таке кут між прямими?
6. Сформулюйте означення перпендикулярних прямих.
7. Які відрізки називають перпендикулярними?
8. Які дві прямі називають паралельними?
9. Які відрізки називають паралельними?
10. За допомогою яких креслярських інструментів можна провести пряму, перпендикулярну до даної прямої? Як це роблять?
11. Як можна провести пряму, паралельну даній прямій?
12. Сформулюйте означення паралельних прямих.
13. Що таке січна двох прямих?
14. Які кути називають внутрішніми різносторонніми? А внутрішніми односторонніми? Покажіть на малюнку.
15. Які кути називають відповідними? Покажіть на малюнку.
16. Сформулюйте і доведіть ознаку паралельності прямих.
17. Сформулюйте аксіому Евкліда про паралельність прямих.
18. Що ви знаєте про Евкліда, про його “Основи”?
19. Сформулюйте і доведіть теорему про внутрішні різносторонні кути при паралельних прямих.
20. Сформулюйте і доведіть властивості відповідних і внутрішніх односторонніх кутів при паралельних прямих і січній.
21. Сформулюйте і доведіть теорему про дві прямі, перпендикулярні до третьої прямої.
22. Що означає слово транзитивний? Сформулюйте теорему про транзитивність паралельності прямих.
23. Що таке теорема? Наведіть приклади теорем.
24. Що таке аксіома? Наведіть приклади аксіом.
25. Що таке означення? Наведіть приклади означень.
26. Яке твердження називають теоремою, оберненою до даної?
27. Що таке ознака?
ГОЛОВНЕ В РОЗДІЛІ 2
Два кути, на які розгорнутий кут розбивається його внутрішнім променем, називають суміжними. Сума мір двох суміжних кутів дорівнює 180°.
Два кути називають вертикальними, якщо сторони одного кута є доповняльними променями сторін другого. Вертикальні кути – рівні.
Якщо дві прямі перетинаються, вони утворюють чотири кути (дві пари вертикальних кутів). Менший із них – кут між даними прямими.
Дві прямі називають перпендикулярними, якщо вони перетинаються під прямим кутом. Якщо прямі а і b перпендикулярні, пишуть: a ⏊ b. Відрізки чи промені називають перпендикулярними, якщо вони лежать на перпендикулярних прямих.
Дві прямі на площині називають паралельними, якщо вони не перетинаються. Якщо прямі a i b паралельні, пишуть: а ‖ b. Два відрізки або промені називають паралельними, якщо вони лежать на паралельних прямих.
Через точку, яка не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній.
Пряму, яка перетинає дві інші прямі, називають їх січною. З двома даними прямими вона утворює 8 кутів, деякі пари яких мають окремі назви:
1 і 3, 2 і 4 – внутрішні різносторонні;
1 і 4, 2 і 3 – внутрішні односторонні;
1 і 8, 2 і 7, 3 і 6, 4 і 5 – відповідні;
5 і 7, б і 8 – зовнішні різносторонні;
5 і 8, б і 7 – зовнішні односторонні.
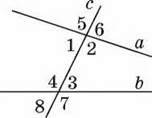
Ознака паралельності прямих
Дві прямі паралельні, якщо з січною вони утворюють рівні внутрішні різносторонні кути, або рівні відповідні кути, або такі внутрішні односторонні кути, сума яких дорівнює 180°.
Властивості паралельних прямих
– Січна з двома паралельними прямими утворює рівні внутрішні різносторонні кути, рівні відповідні кути, такі внутрішні односторонні кути, сума яких дорівнює 180°.
– Дві прямі, паралельні третій, паралельні одна одній.
– Якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до іншої.
Дві прямі, перпендикулярні до третьої, – паралельні.