Головна ⇒ 📌Математика ⇒ ТИПИ СТЕПІНЬ ЧИСЛА

ТИПИ СТЕПІНЬ ЧИСЛА

РОЗДІЛ 4 СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР

У розділі дізнаєтесь:

Що таке степінь числа і як він пов’язаний із дією множення;

Про дію піднесення до степеня та її властивості;

Що таке квадрат і куб числа;

Який порядок виконання дій у виразах, що містять степені;

Що таке многокутник та які його види;

Як обчислювати площу прямокутника і квадрата;

Що таке прямокутний паралелепіпед, куб, піраміда;

Як обчислювати об’єм прямокутного паралелепіпеда і куба;

Що таке комбінаторна

задача та як її розв’язувати;

Як застосувати вивчений матеріал на практиці

§ 18. СТЕПІНЬ ЧИСЛА

Ви вже знаєте, що суму кількох рівних доданків можна знайти за допомогою дії множення. Наприклад:

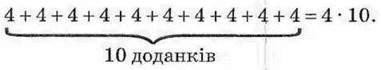
Про таку числову рівність кажуть, що суму рівних доданків згорнули в добуток. І навпаки, якщо читати цю рівність справа наліво, виходить, що добуток 4 ∙ 10 розгорнули в суму рівних доданків.

? Чи можна згорнуто записати добуток кількох рівних множників, наприклад, 4∙4∙4∙4∙4∙4∙4∙4∙4∙4? Так. Для цього використовують спеціальний вираз 410, який

називають степенем.

? Вираз 410 читають так: “чотири в десятому степені” або “десятий степінь числа 4”.

У виразі 410 число 4 називають феновою степеня – вона показує, яке число множили саме на себе. Число 10 називають показником степеня – він показує, скільки рівних множників було в добутку. Отже, добуток рівних множників можна згорнути в степінь:

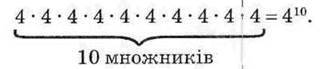
Дію, за допомогою якої добуток рівних множників згортають у степінь, називають піднесенням до степеня. Це – п’ята арифметична дія.

Піднести число а до степеня п означає знайти добуток n множників, кожен з яких дорівнює а.

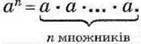
Задача. Порівняйте значення степенів 410 і 104

Розв’язання. Піднесемо число 4 до степеня 10:

410= 4∙4∙4∙4∙4∙4∙4∙4∙4∙4=1048576.

Піднесемо число 10 до степеня 4:

104= 10 ∙ 10 ∙ 10 ∙ 10= 10000.

Оскільки 1048576 > 10000, то 410 > 104.

Зверніть увагу:

Значення степеня може змінитися, якщо поміняти місцями основу степеня та його показник.

? Чи існує степінь, значення якого не зміниться, якщо його основу і показник поміняти місцями? Так. Наприклад, 33, 2525, 428428.

Якщо основа степеня дорівнює 1, то значення степеня при будь-якому натуральному n дорівнює 1:

1n = 1

Наприклад, 12 = 1, 125 = 1, 1257 = 1.

Якщо показник степеня дорівнює 1, то значення степеня при будь-якому натуральному а дорівнює а:

А1 = а.

Наприклад, 21 = 2, 251= 25, 2571= 257.

Нова арифметична дія – піднесення до степеня – вносить зміни до порядку виконання дій. Це дія третього ступеня, тому її виконують найпершою.

Задача. Обчисліть значення виразу З6 + 2 ∙ 132- 8 : 4.

Розв’язання.

Визначимо порядок виконання дій у заданому виразі:

1 5 3 2 6 4

36 + 2 ∙ 132 – 8 : 4,

Тепер виконаємо дії у цьому порядку;

З6 + 2 ∙ 132- 8 : 4 = 729 + 2 ∙ 169-8:4 = 729 + 338-2=1065.

Зверніть увагу:

У виразах, що містять степені, спочатку виконують піднесення до степеня, а потім множення і ділення, додавання і віднімання.

Особливими вважають другий і третій степені числа. Для них навіть придумали власні назви: другий степінь називають квадратом числа, а третій степінь – кубом цього числа.

Степінь а2 читають так: “а в квадраті”, а степінь а3 – “а в кубі”.

Для спрощення обчислень важливо запам’ятати квадрати і куби одноцифрових чисел. Відповідну таблицю розміщено на форзаці підручника.

Дізнайтеся більше

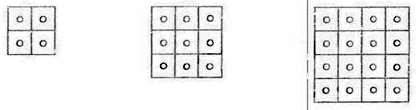
Існує цікава закономірність, що пов’язує квадрат натурального числа і квадрат попереднього для нього натурального числа. Подивіться на малюнок 148. Ви бачите, як за допомогою квадратиків із червоними і чорними кружечками можна унаочнити числові рівності:

22 = 1 + 3 , 32 = 1 +3 + 5, 42=1+3 + 5 + 7 і т. д.

Звідси:

22 = 12 + 3, 32 = 22 + 5, 42 = 32 + 7.

Мал. 148

РОЗВ’ЯЖІТЬ ЗАДАЧІ

569. Прочитайте вираз: 1) 22; 2) 25; 3) 32; 4) 43; 5) 674; 6) 1002. Назвіть основу і показник степеня. Що вони показують?

670. Скільки разів взято множником число 5, якщо отримали степінь:

1) 52; 2) 55; 3) 545; 4)5n; 5) 5m?

671. Якому степеню числа 2 дорівнюй добуток:

1)2∙2∙2; 3)2∙2∙2∙2;

2)2∙2 ∙ 2 ∙ 2 ∙ 2; 4) 2?

671. Якими даними треба доповнити клітинки таблиці 25?

Таблиця 25

Степінь

Основа

Степеня

Показник

Степеня

100

673. Чи правильно визначено порядок дій у виразі:

1 2 1 2 12 3 1 2

1) 43 + 9; 2) 23 – 23; 3)5∙32∙7; 4)82:4?

674. Запишіть у вигляді степеня:

1) три у квадраті; 2) шістнадцять у кубі.

675 Яка з рівностей є правильною:

1) 5 + 5 + 5 = 53; 2) 5 ∙ 5 ∙ 5 = 53; 3)5∙3 = 53?

676. Запишіть у вигляді степеня:

1) 37 ∙ 37 ∙ 37 ∙ 37 ∙ 37 ∙ 37; 3) m ∙ m ∙ m;

2) 24 ∙ 24 ∙ 24 ∙ 24 ∙ 24 ∙ 24 ∙ 24; 4) n∙ n ∙ n ∙ n ∙ n ∙ n ∙ n ∙ n ∙ n.

677. Запишіть у вигляді добутку:

1) 275; 2) 5394; 3) m6; 4) n12.

678. За даними таблиці 26 знайдіть значення степеня з основою 10. Яка простежується закономірність?

Таблиця 26

Степінь

101

102

103

104

105

106

107

108

10а

1010

Значення

Степеня

679°. Порівняйте значення виразів:

1)3 + 3 + 3 і 3∙3∙3; 2) 3 ∙ 2 і З2.

680. Поставте знаки “<“, “>”, або “=” між виразами:

1) 23 і З2; 3) 12 і 13; 5)231 і 321; 7) 26 і 134;

2) 25 і 52; 4) 123 і 132; 6)1231 і 1321; 8) 80 і З4.

681. Обчисліть:

1)111 ∙ 11; 2) 54 + 75; 3) 122 : 6; 4) 23 ∙ 52.

682. Обчисліть:

1) 350 – б2 ∙ 3; 3) (350 – 6)2 ∙ 3;

2) (350 – б2)∙3; 4) 350 – (6 ∙ З)2.

683. Визначте порядок дій у виразі:

1) 26+ 2 ∙ 52 ∙ 7; 2) (26 + 2) ∙ 52 ∙ 7; 3) 342 +52∙З2∙7.

684. Знайдіть а2, якщо а дорівнює: 1) 12; 2) 25; 3) 100.

685. Знайдіть m3, якщо m дорівнює: 1) 8; 2) 15; 3) 100.

686. За даними таблиці 27 знайдіть квадрати і куби числа а. Запам’ятайте отримані значення.

Таблиця 27

A	1	2	3	4	5	6	7	8	9	10
A2
А3

687. Яке число у квадраті дорівнює: 1) 100; 2) 64; 3) 49?

688. Яке число в кубі дорівнює: 1) 8; 2) 125; 3) 64?

689. Запишіть у вигляді виразу:

1) сума квадрата числа 3 і числа 6;

2) різниця куба числа 5 і числа 100.

690. Розв’яжіть рівняння:

1) 24 – х = 10; 3)54 + х = 625;

2) 300 – х= б3; 4)4х = 82.

691. Запишіть вираз у вигляді степеня з основою 2:

1)8 ∙ 4; 2)2∙4∙16; 3)32∙2∙64.

692 Запишіть вираз у вигляді степеня:

1) 9 ∙ 9 ∙ 9 ∙ 3 ∙3 ∙ 3; 2) 25 ∙ 25 ∙ 125 ∙ 125 ∙ 125 ∙ 25.

693. Запишіть вираз у вигляді добутку та обчисліть його значення:

1) 31 ∙ З2; 2) 63∙62; 3) 52 ∙ 52.

694. Запишіть у вигляді степеня вираз:

1) 26 ∙ 24; 2) 88 ∙ 82; 3) а2 ∙ а8; 4)р3∙р27.

695. Обчисліть:

1) 2 ∙ 54 + 12 ∙ 63+12 ∙ З2; 3) 152 : (63+З2);

2) (2 ∙ 54 – 2): 23; 4) (23 ∙ 33): (22 ∙ З2).

696. Обчисліть:

1) 54- 22 ∙ 6 + 43; 3)(54-22) 6+43;

2) (54 – 22 ∙ 6) + 43; 4)54 – 22 ∙ (6 + 43).

697.Знайдіть значення виразу а + b2, якщо b = 8, а а дорівнює:

1)1; 2)6; 3)100.

698. Знайдіть значення виразу (а + b)2, якщо a = 2,ab дорівнює:

1)12; 2)5; 3)10.

699. Знайдіть значення виразу а2 + b2, якщо а = 2, а b дорівнює:

1)12; 2)5; 3)10.

700. Знайдіть:

1) куб суми квадратів чисел 3 і 4;

2) квадрат різниці кубів чисел 6 і 5.

701. Розв’яжіть рівняння:

1) 23 ∙ х = б4; 2) 32+х=25; 3)27-х=53.

702. Число 7065 можна записати як суму розрядних доданків:

7065 = 7 ∙ 1000+6 ∙ 10+5 = 7 ∙ 103 + 6 ∙ 101+ 5. Запишіть у такому вигляді число:

1) 4567; 2) 30003.

703. Запишіть у вигляді степеня:

1)4∙ 27∙9∙ 64∙3∙16; 2) 11 ∙11∙ 8 ∙11 ∙ 11 ∙21 .

704. Розв’яжіть рівняння:

1) 24 ∙ х = б3- 40; 3) (54 – х2) ∙ 23 = 63+ 24;

2) 25 ( 25- х) – 53; 4) 112-х2= 102-22∙52.

705. Обчисліть:

1) 4∙104+4 ∙ 103+4 ∙ 102 + 4 ∙ 1044;

2) 105+ 2 ∙ 103 + 7 ∙ 102 + 3 ∙ 101+6.

Яка закономірність простежується?

706. Знайдіть суму чисел:

1) 2 ∙ 105+ 3 ∙ 104 + 4 ∙ 103+ 5 ∙ 102 + 6 ∙ 101 + 7 і 5 ∙ 106 + 9 ∙ 104+ 102+ 8 ∙ 101 + 3;

2) 4 ∙ 105+ 5 ∙ 104+ 7 ∙ 103+ 6 ∙ 101 + 7 і 5 ∙106+ 5 ∙ 104+ 102 + 3.

707. Знайдіть різницю куба суми квадратів чисел 2 і 3 та квадрата суми кубів цих чисел.

708. Задача Ал-Хорезми( Середня Азія, близько 780р. -850р.). Подайте число 10 у вигляді двох натуральних доданків, сума квадратів яких дорівнює 58.

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

709. На першу клітинку шахової дошки поклали 2 зернятка, на другу – у 2 рази більше, ніж на першу, на третю – у 2 рази більше, ніж на другу і т. д. Скільки зерняток буде на: 1) десятій клітинці; 2) на останній клітинці? Відповідь запишіть у вигляді степеня числа 2.

ЗАДАЧІ НА ПОВТОРЕННЯ

710. Обчисліть усно:

1) 125:5 + 24∙2-15; 2)56:7 + 52 +4∙15.

711. Розв’яжіть рівняння:

1) (25-х) ∙ 11 = 169 : (67- 54)-458 : 229;

2) 16х – 34 = 405 : 5 – 153 : З,

712. Даринка купила 15 зошитів по 1 грн 30 к. та 4 альбоми по 7 грн. Скільки заплатила за покупку Даринка?

713. Олексій купив 5 пачок морозива по 0 грн 50 к. та 6 пачок печива по 6 грн 25 к. Скільки заплатив за покупку Олексій?