Точка та прямі
§ 1. Найпростіші геометричні фігури та їхні властивості
1. Точка та прямі
Практичні завдання
1.
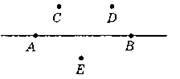
2. Прямі ME, МК, ЕК, EM, КМ, КЕ.

3. Точка С належить прямій а, точка С належить прямій b.
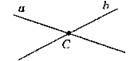
4. Утворилося три прямих.
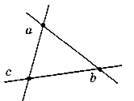
5.

6. Можна отримати три або одну точку перетину.
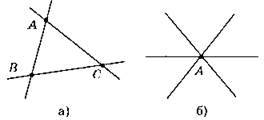
7. 1)

2)
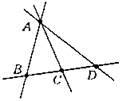
3)
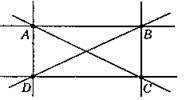
Вправи
8. 1) Прямій а належать точки С, D, Е; прямій МК належать точки М, К, Е.
2) Прямій а не належать точки В, F, К, Р; прямій МК не належать точки С, D, B, F, Р.
3) Прямі а і МК перетинаються в точці Е.
4) Точки, які належать прямій а, але не належать прямій МК: В, Р, F.
9. 1) Точки, що належать прямій р: В, Е, А; точки, які не належать прямій р: C, D.
2) Точка А належить прямим m, р, k, АС; точка В належить прямим n і р; точка D належить прямим k i n, DE; точка Е належить прямим р, EC, BE.
3) Через точку С проходять прямі: n, СЕ, СА; через точку В проходять прямі: n, р; через точку D проходять прямі: n, СА, СЕ; через точку Е проходять прямі:
4) Прямі kip перетинаються в точці А; прямі m і k перетинаються в точці А.
5) Три із чотирьох зображених на рисунку прямих перетинаються в точці А.
10. Прямі AB і АС рівні, оскільки при накладанні вони співпадають.
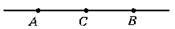
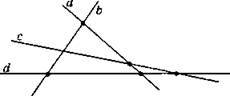
11. Серед прямих а, b, с, d кожні дві з них перетинаються, причому через кожну точку перетину проходять тільки дві прямі. При цьому утвориться б точок перетину.
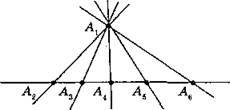
12. Шість точок A1, А2, А3, А4, А5, А6 визначають шість прямих: A1А2; A1А3; A1А4; A1А5; A1А6; A2А6.
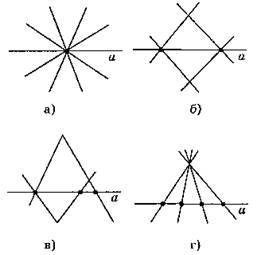
13. Якщо дану пряму а перетинають чотири прямі, то може утворитися або 1, або 2, або 3, або 4 точки перетину з даною прямою.
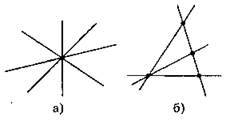
14. Якщо провели чотири прямі, кожні дві з яких перетинаються, то може утворитися 1 або 4, або б точок перетину.
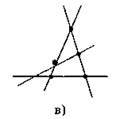
15. Якщо провели п’ять прямих, кожні дві з яких перетинаються, то найменша кількість точок перетину цих прямих дорівнює 1; а найбільша кількість точок перетину цих прямих дорівнює 10.
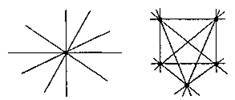
16. Можна провести шість прямих і позначити на них 11 точок так, щоб на кожній прямій було позначено рівно чотири точки.

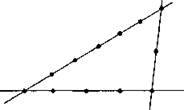
17. Якщо на площині проведено три прямі і на першій прямій позначено п’ять точок, на другій сім точок, а на третій – три точки, то найменша кількість точок становить 12 (перша і друга, друга і третя, перша і третя прямі перетинаються: (5 + 7 + 3 – 3= 12).
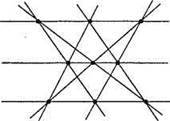
18. Можна позначити дев’ять точок і провести дев’ять прямих так, щоб на кожній прямій лежало рівно три позначені точки і через кожну точку проходило рівно три з проведених прямих.
Спостерігайте, рисуйте, конструюйте, фантазуйте
19.
