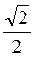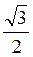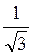Тригонометричні функції числового аргументу
УРОК 7
Тема. Тригонометричні функції числового аргументу
Мета уроку: Формування поняття тригонометричних функцій числового аргументу; вивчення значень тригонометричних функцій деяких чисел (кутів), зміни знаків тригонометричних функцій у координатних чвертях.
І. Перевірка домашнього завдання
Розв’язування вправ аналогічних до домашніх.
1. Подайте в радіанній мірі кути:
А) 5°; б) 1140°; в) -765°; г) 67° 5′.
Відповідь: а) 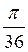 ; б)
; б) 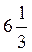 ?; в)
?; в) 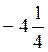 ?; г)
?; г) 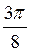
2. Подайте в градусній мірі кути:
А) 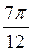 ; б) 1,25?; в) 1; г) 10.
; б) 1,25?; в) 1; г) 10.
Відповідь: а) 105°; б) 225°; в) 57,32°; г) 573,25°.
3. Знайдіть довжину дуги, якщо на неї опирається центральний кут? = 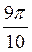 , а радіус кола дорівнює 10 м.
, а радіус кола дорівнює 10 м.
Відповідь: 9? м.
II. Сприймання і усвідомлення понять синуса, косинуса, тангенса і котангенса числа
Розглянемо на координатній площині коло радіуса 1 з центром у початку координат, яке називається одиничним (рис. 43). Позначимо точку Ро – правий кінець горизонтального діаметра. Поставимо у відповідність кожному дійсному числу? точку кола за такими правилом:
1)
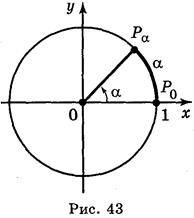
2) Якщо? < 0, то, рухаючись із точки? о (рис. 44) в напрямі за годинниковою стрілкою, опишемо по колу шлях довжиною |?|; кінець цього шляху і буде шукана точка Р?.
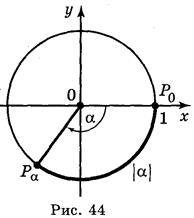
3) Якщо? = 0, то поставимо у відповідність точку Ро.
Таким чином, кожному дійсному числу можна поставити у відповідність точку?0 одиничного кола.
Якщо? = ?о + 2?k, де k – ціле число, то при повороті на кут? одержуємо одну і ту саму точку, що й при повороті на кут? о.
Якщо точка? відповідає числу?, то вона відповідає і всім числам виду? + 2?k, де 2? – довжина кола (бо радіус дорівнює 1), а k – ціле число, що показує кількість повних обходів кола в ту чи іншу сторону.
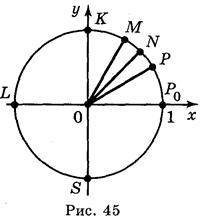
1. Яким числам відповідають точки Р0, Р, М, K, L, S (рис. 45), якщо відомо, що? – середина дуги Р0К, а дуги Р0Р, РМ, МК – рівні.
Відповідь: 2?n;  +2?n;
+2?n;  +2?n;
+2?n;  + 2?n;
+ 2?n;  + 2?n; ? + 2?n; –
+ 2?n; ? + 2?n; –  + 2?n, n
+ 2?n, n  Z.
Z.
2. Позначте на одиночному колі точки, які відповідають числам:
А)  + 2?n, –
+ 2?n, –  + 2?n,
+ 2?n, 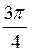 + 2?n, –
+ 2?n, –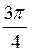 + 2?n, де n
+ 2?n, де n  ?;
?;
Б)  + 2?n,
+ 2?n, + 2?n,
+ 2?n, 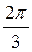 + 2?n,
+ 2?n, 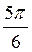 + 2?n, –
+ 2?n, – 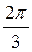 + 2?n, де n
+ 2?n, де n  ?.
?.
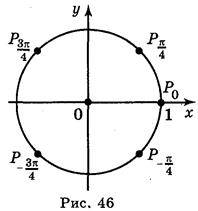
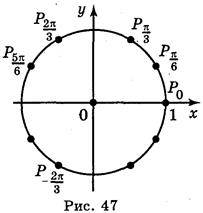
Відповідь: а) рис. 46 (кожна чверть кола поділена на 2 рівні частини); б) рис. 47 (кожна чверть кола поділена на 3 рівні частини).
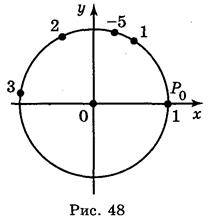
3. Позначте на одиночному колі точки, які відповідають числам 1; 2; 3;-5. Відповідь: рис. 48.
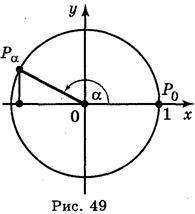
Синусом числа? називається ордината точки Р?, утвореної поворотом точки Р? (1; 0) навколо початку координат на кут в? радіан (позначається sin?) (рис. 49).
Синус визначений для будь-якого числа?.
Косинусом числа? називається абсциса точки Р?, утвореної поворотом точки Р? (1; 0) навколо початку координат на кут в? радіан (позначається cos?) (рис. 49).
Косинус визначений для будь-якого числа?.
Виконання вправ
1. Обчисліть:
A) cos 7?; б) sin 7?; в) cos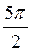 ; г) sin
; г) sin 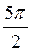 .
.
Відповідь: а) -1; б) 0; в) 0; г) 1.
2. Обчисліть:
A) 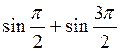 ; б)
; б) 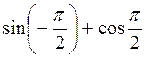 ; в) sin? + sin 1,5?; г) cos0 + cos 3,5? – cos 3?.
; в) sin? + sin 1,5?; г) cos0 + cos 3,5? – cos 3?.
Відповідь: а) 0; б) -1; в) -1; г) 2.
Тангенсом числа? називається відношення синуса числа? до його косинуса: 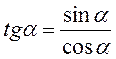 .
.
Тангенс визначений для всіх а, крім тих значень, для яких cos? = 0, тобто, ? =  + ?n, n
+ ?n, n  ?.
?.
Для розв’язування деяких задач корисно мати уявлення про лінію тангенсів (рис. 50). Проведемо дотичну t до одиничного кола в точці? о. Нехай? – довільне число, для якого cos? 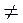 0, тоді точка Р? (cos?; sin?) не лежить на осі ординат і пряма ОР? перетинає t в деякій точці Т? з абсцисою 1. Знайдемо ординату точки Т? із трикутника ОРоТ?.
0, тоді точка Р? (cos?; sin?) не лежить на осі ординат і пряма ОР? перетинає t в деякій точці Т? з абсцисою 1. Знайдемо ординату точки Т? із трикутника ОРоТ?.
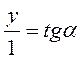 ; у = tg?.
; у = tg?.
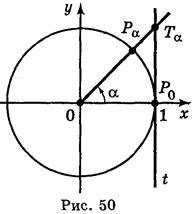
Таким чином, ордината точки перетину прямих ОР? і t дорівнює тангенсу числа?. Тому пряму t називають віссю тангенсів.
Котангенсом числа? називається відношення косинуса числа? до його синуса: 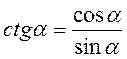 .
.
Котангенс визначений для всіх?, крім таких значень, для яких sin? 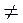 0, тобто, a = ?n, n
0, тобто, a = ?n, n  ?.
?.
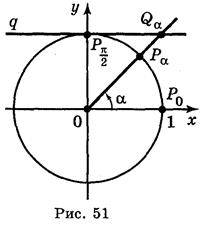
Введемо поняття лінії котангенсів (рис. 51). Проведемо дотичну q до одиничного кола в точці 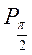 . Для довільного числа?, якщо sin?
. Для довільного числа?, якщо sin? 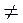 0 і відповідно точка Р? (cos?, sin?) не лежить на осі ОХ і тому пряма ОР? перетинає пряму q у деякій точці Q? з ординатою, що дорівнює 1. Із трикутника О
0 і відповідно точка Р? (cos?, sin?) не лежить на осі ОХ і тому пряма ОР? перетинає пряму q у деякій точці Q? з ординатою, що дорівнює 1. Із трикутника О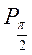 Q? маємо:
Q? маємо: 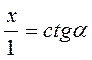 , звідси х = ctg?. Таким чином, абсциса точки перетину прямої ОР? і q дорівнює котангенсу числа?, тому пряму q називають віссю котангенсів.
, звідси х = ctg?. Таким чином, абсциса точки перетину прямої ОР? і q дорівнює котангенсу числа?, тому пряму q називають віссю котангенсів.
Виконання вправ
1. Обчисліть: а) tg?; б) tg (-?); в) tg 4?; г) tg 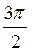 .
.
Відповідь: а) 0; б) 0; в) 0; г) не визначений.
2. Визначте знак числа: а) tg 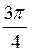 ; б) tg
; б) tg 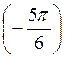 ; в) tg
; в) tg 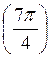 ; г) ctg
; г) ctg 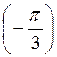 .
.
Відповідь: а) мінус; б) плюс; в) мінус; г) мінус.
III. Визначення значень тригонометричних функцій деяких чисел
Через те що поворот на кут в? радіан співпадає з поворотом 180 на кут –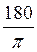 ? градусів, аргумент синуса і косинуса можна виразити як в градусах, так і в радіанах. Наприклад, при повороті точки (1; 0) на кут
? градусів, аргумент синуса і косинуса можна виразити як в градусах, так і в радіанах. Наприклад, при повороті точки (1; 0) на кут  , тобто на кут 90?, тому sin
, тобто на кут 90?, тому sin = sin 90° = 1, cos
= sin 90° = 1, cos = cos 90° = 0.
= cos 90° = 0.
Заповнимо таблицю значень синуса, косинуса, тангенса і котангенса деяких чисел (таблиця 4) або розглянемо таблицю 2 (стор. 31) підручника і виконаємо вправу 1.
? | 0 |
|
|
|
| ? |
| 2? |
0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° | |
Sin? | 0 |
|
|
| 1 | 0 | -1 | 0 |
Cos? | 1 |
|
|
| 0 | -1 | 0 | 1 |
Tg? | 0 |
| 1 |
| Не існ. | 0 | Не існ. | 0 |
Ctg? | Не існ. |
| 1 |
| 0 | Не існ. | 0 | Не існ. |
Значення синуса, косинуса, тангенса і котангенса інших чисел можна знайти за допомогою математичних таблиць або калькулятора.
1. Обчисліть:
А) 3sin  + 2cos
+ 2cos  – tg
– tg  ;
;
Б) 5sin  +3tg
+3tg  – 5cos
– 5cos  – 10ctg
– 10ctg  ;
;
В) 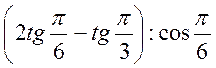 ;
;
Г) sin  ? cos
? cos  – tg
– tg  .
.
Відповідь: а) 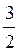 ; б)-7; в) –
; б)-7; в) –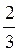 ; г) –
; г) –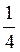 .
.
2. Обчисліть за допомогою мікрокалькулятора: а) sin 1,5; б) cos 0,5; в) tg 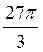 ; г) сtg
; г) сtg 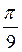 .
.
Відповідь: а) 1,00; б) 0,88; в) 3,08; г) 2,75.
IV. Вивчення зміни знаків тригонометричних функцій
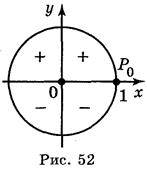
Число sin? – це ордината відповідної точки Р?, тому sin? > 0, якщо точка розташована вище осі абсцис, тобто в І і II чвертях (рис. 52). Якщо ця точка лежить нижче осі абсцис, то її ордината від’ємна в третій і четвертій чвертях.
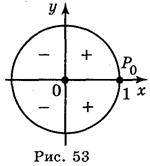
Число cos? – це абсциса точки Р?, тому cos? > 0 в І та IV чвертях, cos? < 0 в II та III чвертях (рис. 53).
Так як 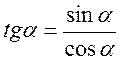 ,
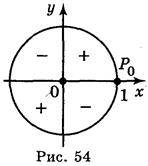
, 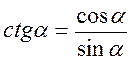 , то tg? > 0 і ctg? > 0, якщо sin? і cos? мають однакові знаки, тобто в І і III чвертях, і tg? < 0 і ctg? < 0 в II і IV чвертях (рис. 54).
, то tg? > 0 і ctg? > 0, якщо sin? і cos? мають однакові знаки, тобто в І і III чвертях, і tg? < 0 і ctg? < 0 в II і IV чвертях (рис. 54).
1. У якій чверті знаходиться точка??, якщо:
А) sin? > 0 і cos? > 0;
Б) sin? > 0 і cos? < 0;
В) sin? < 0 і cos? > 0;
Г) sin? < 0 і cos? < 0?
Відповідь: а) І; б) II; в) IV; г) III.
2. Якій чверті належить Р?, якщо:
А) sin? cos? > 0;
Б) sin? cos? < 0;
В) tg? cos? > 0;
Г) ctg? sin? < 0?
Відповідь: а) І або III; 6) II або IV; в) І або II; г) II або III.
3. Знайдіть знак виразу:
А) cos 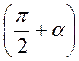 ; б) sin
; б) sin 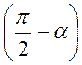 ; в) ctg (? + ?); г) tg
; в) ctg (? + ?); г) tg 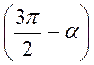 , якщо 0 < ? <
, якщо 0 < ? <  .
.
Відповідь: а) мінус; б) плюс; в) плюс; г) плюс.
4. Визначте знак виразу:
А) sin105° – cos105°; б) cos155° – sin255°; в) tg127° – ctg200°; г) tg351° – ctg220°.
Відповідь: а) мінус; б) плюс; в) мінус; г) мінус.
5. Визначте знак добутку:
А) tg 2 – tg 3 – ctg 3 – cos 1; б) sin 1 – cos 2 – tg 3 – ctg 4.
Відповідь: а) мінус; б) плюс.
V. Підсумок уроку
VI. Домашнє завдання
Розділ І § 4. Запитання і завдання для повторення до розділу І № 40-42, 46. Вправи № 10, 12, 16, 21.