Головна ⇒ 📌ГДЗ з математики ⇒ Вертикальні кути

Вертикальні кути

Розділ 1. Найпростіші геометричні фігури та їх властивості

§ 5. Вертикальні кути

152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні.

153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1.

154.

Вертикальні кути

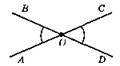
∠BOA і ∠COD – суміжні.

∠BOA = ∠COD = 60°.

155. 1)

Вертикальні кути

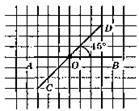
∠DOB = ∠COA = 45°;

2)

Вертикальні кути

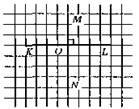
∠MOL = ∠NOK = 90°.

156. ∠AOB = ∠DOC = 41°; ∠KOL = ∠MON = 149°.

157.

Вертикальні кути

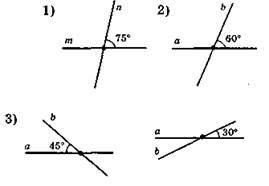
158.

∠1

12°

121°

34°

143°

156°

65°

178°

87°

∠2

12°

121°

34°

143°

156°

65°

178°

87°

Кут

між прямими

Так

Ні

Так

Ні

Ні

Так

Ні

Так

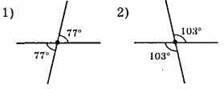
159. Мал. 97. α + α = 100°; 2α = 100°; α = 100° : 2 = 50°.

Мал. 98. β + β – 220°; 2β = 220°; β = 220° : 2 = 110°.

Відповідь: 50° і 50°; 110° і 110°.

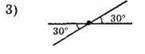
160. 1) 30° : 2 = 15°. Отже, вертикальні кути дорівнюють

15° і 15°.

2) 211° : 2 = 105°30′. Отже, вертикальні кути дорівнюють 105°30′ і 105°30′.

3) 67° : 2 = 33°30′. Отже, вертикальні кути дорівнюють 33°30′ і 33°30′.

4) 190° : 2 = 95°. Отже, вертикальні кути дорівнюють 95° і 95°.

161. Вертикальні кути можуть бути:

1) гострими β < 90°;

Вертикальні кути

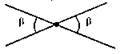
2) тупими 90° < β < 90°;

Вертикальні кути

3) прямими β = 90°.

Вертикальні кути

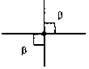
162. Мал. 99. ∠BOC = ∠DOA = 130°- як вертикальні кути;

∠BOD = 180° – ∠BOC = 180° – 130° = 50° – як суміжні кути;

∠AOC = ∠BOD = 50° – як вертикальні кути.

Відповідь: 130°; 50°; 50°.

Мал. 100. ∠COA = ∠BOD = 72° – як вертикальні кути;

∠BOC = 180° – ∠BOD = 180° – 72° = 108° – як суміжні кути;

∠DOA = ∠BOC = 108° – як вертикальні кути.

Відповідь: 72°; 108°; 108°.

163.

Вертикальні кути

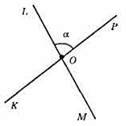
Якщо ∠LOP = α, то ∠KOM = α – як вертикальні кути; ∠KOL = ∠MOP – як вертикальні кути; ∠KOL = 180° – ∠LOP = 180° – α.

1) Якщо α = 40°, то ∠КОМ = 40°, ∠KOL = ∠MOP = 180° – 40° = 140°;

2) якщо α = 12°, то ∠KOM = 12°, ∠KOL = ∠MOP = 180° – 12° = 168°;

3) якщо α = 25°, то ∠KOM = 25°, ∠KOL = ∠MOP = 180° – 25° = 155°.

4) якщо α = 17°, то ∠KOM = 17°, ∠KOL = ∠MOP = 180° – 17° = 163°.

Відповідь: 1) 40°, 140°, 140°; 2) 12°, 168°, 168°; 3) 25°, 155°, 155°; 4) 17°, 163°, 163°.

164. 1) Менший кут дорівнює (180° – 14°) : 2 = 83°, більший дорівнює 180° – 83° = 97°. Отже, утворилися кути: 83°, 97°, 83°, 97°.

2) Менший кут дорівнює (180° – 56°) : 2 = 62°, більший дорівнює 180° – 62° = 118°. Отже, утворилися кути: 62°, 118°, 62°, 118°.

3) Менший кут дорівнює (180° – 38°) : 2 = 71°, більший дорівнює 180° – 71° = 109°. Отже, утворилися кути: 71°, 109°, 71°, 109°.

4) Менший кут дорівнює (180° – 70°) : 2 = 55°, більший дорівнює 180° – 55° = 125°. Отже, утворилися кути; 55°, 125°, 55°, 125°.

165. Вертикальні кути: ∠LFD і ∠AFB, ∠LFD i ∠DFB.

Суміжні кути: ∠LFD і ∠AFL, ∠LFD і ∠DFВ, ∠AFB і ∠LFA, ∠AFB і ∠BFD.

166. Вертикальні кути: ∠AOD і ∠BOL, ∠AOL і ∠DOB.

167.

Вертикальні кути

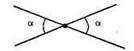
Оскільки вертикальні кути рівні і їх сума більша за один із них на а, то вертикальні кути дорівнюють: 1) 45° і 45°; 2) 90° і 90°; 3) 109° і 109°; 4) 130° і 130°.

168.

Вертикальні кути

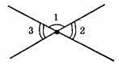
1) Якщо ∠1 = 105°, то ∠2 = 180° – 105° = 75°. ∠2 + ∠3 = 75° х 2 = 150°.

2) Якщо ∠1 = 71°30′, TO ∠2 = 180° – 71°30′ = 108°30′. ∠2 + ∠3 = 2 х 108°30′ = 217°.

3) Якщо ∠1 = 93°35′, TO ∠2 = 180° – 93°35′ = 86°25′. ∠2 + ∠3 = 2 x 86°25′ = 172°50′.

4) Якщо ∠1 = 120°45′, то ∠2 = 180° – 120°45′ = 59°15′. ∠2 + ∠3 = 2 х 59°15′ = 118°30′.

Відповідь: 1) 150°; 2) 217°; 3) 172°50′; 4) 118°30′.

169.

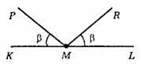
Вертикальні кути

Вертикальні кути

170.

Вертикальні кути

Так, кути можуть бути рівними, але не бути вертикальними. Наприклад: ∠KMP = ∠LMR = β, але ∠KMP і ∠LMR не вертикальні.

171. Два нерівні кути не можуть бути вертикальними, оскільки вертикальні кути рівні.

172. Вертикальні кути: ∠LAD і ∠CAB, ∠LAC і ∠DAB, ∠KCQ і ∠ACB, ∠KCA і ∠QCB, ∠CBA і ∠EPF, ∠CBF і ∠ABE.

173.

Вертикальні кути

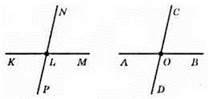
Нехай ∠NLM = ∠COB, тоді ∠KLP = ∠NLM-як вертикальні кути, ∠AOD = ∠COB-як вертикальні кути. Оскільки ∠NLM = ∠COB – за умовою, то ∠KLP = ∠AOD. Отже, якщо два кути рівні, то вертикальні з ними також рівні.

174. Утворилося 6 пар вертикальних кутів: ∠KCM і ∠DCL, ∠KCB і ∠ACL, ∠MCB і ∠ACB, ∠MCL і ∠DCK, ∠BCL і ∠ACK, ∠BCD і ∠ACM.

Утворилося 12 пар суміжних кутів: ∠ACK і ∠KCB, ∠ACM і ∠MCB, ∠ACD і ∠DCB, ∠ACL і ∠LCB, ∠DCA і ∠ACM, ∠DCK і ∠KCM, ∠DCL і ∠LCM, ∠DCB і ∠BCM, ∠KCM і ∠MCL, ∠KCB і ∠BCL, ZKCA і ∠ACL, ∠KCD і∠DCL.

175. При перетині двох прямих утворюється дві пари вертикальних кутів і чотири пари суміжних кутів. Сума будь-яких суміжних кутів дорівнює 180°, а сума двох вертикальних кутів відмінна від 180°. Отже, за умовою задачі задана сума вертикальних кутів.

1) Один із кутів дорівнює 102° : 2 = 51°, а суміжний з ним кут дорівнює 180° – 51° = 129°. Отже, утворені кути дорівнюють: 51°, 129°, 51°, 129°.

2) Один із кутів дорівнює 320° : 2 = 160°, тоді суміжний з ним кут дорівнює 180° – 160° = 20°. Отже, утворені кути дорівнюють: 160°, 20°, 160°, 20°.

3) Один із кутів дорівнює 238° : 2 = 119°, тоді суміжний з ним кут дорівнює 180° – 119° = 61°. Отже, утворені кути дорівнюють: 119°, 61°, 119°, 61°.

4) Один із кутів дорівнює 182° : 2 = 91°, тоді суміжний з ним кут дорівнює 180° – 91° = 89°. Отже, утворені кути дорівнюють: 91°, 89°, 91°, 89°.

Відповідь: 1) 51°, 129°, 51°, 129°; 2)160°, 20°, 160°, 20°; 3) 119°, 61°, 119°, 61°; 4) 91°, 89°, 91°, 89°.

176. При перетині двох прямих утворилося дві пари вертикальних кутів і чотири пари суміжних кутів. Різниця двох вертикальних кутів дорівнює 0°, а різниці двох суміжних кутів (відмінних від прямих) відмінна від 0°. Отже, за умови задачі задана різниця суміжних кутів.

1) Менший кут дорівнює (180° – 29°) : 2 = 75°30′, тоді більший кут дорівнює 180° – 75°30′ = 104°30′. Отже, утворилися кути: 75°30′, 75°30′, 104°30′, 104°30′.

2) Менший кут дорівнює (180° – 115°) : 2 = 32°30′, тоді більший кут дорівнює 180° – 32°30′ = 147°30′. Отже, утворилися кути: 32°30′, 32°30′, 147°30′, 147°30′.

3) Менший кут дорівнює (180° – 107°) : 2 = 36°30′, тоді більший кут дорівнює 180° – 36°30′ = 143°30′. Отже, утворилися кути: 36°30′, 36°30′, 143°30′, 143°30′.

4) Менший кут дорівнює (180° – 53°) : 2 = 63°30′, тоді більший кут дорівнює 180° – 63°30′ = 116°30′. Отже, утворилися кути: 63°30′, 63°30′, 116°30′, 116°30′.

Відповідь: 1) 75°30′, 75°30′, 104°30′, 104°30′; 2) 32°30′, 32°30′, 147°30′, 147°30′; 3) 36°30′, 36°30′, 143°30′, 143°30′; 4) 63°30′, 63°30′, 116°30′, 116°30′.

177. При перетині двох прямих утворюється дві пари вертикальних кутів і чотири пари суміжних кутів. Частка двох вертикальних кутів дорівнює 1 (оскільки вертикальні кути рівні), а частка двох суміжних кутів (відмінних від прямих) не дорівнює 1. Отже, за умовою задачі задана частка суміжних кутів.

1) Менший кут дорівнює 180° : 10 х 1 = 18°, а більший кут – 180° : 10 х 9 = 162°. Отже, утворилися кути: 18°, 18°, 162°, 162°.

2) Менший кут дорівнює 180° : 12 х 1 = 15°, а більший кут дорівнює 180° : 12 х 11 = 165°. Отже, утворилися кути: 15°, 15°, 165°, 165°.

3) Менший кут дорівнює 180° : 6 х 1 = 30°, а більший кут дорівнює 180° : 6 х 5 = 150°. Отже, утворилися кути: 30°, 30°, 150°, 150°.

4) Менший кут дорівнює 180° : 18 х 1 = 10°, а більший кут дорівнює 180° : 18 х 17 = 170°. Отже, утворилися кути: 10°, 10°, 170°, 170°.

Відповідь: 1) 18°, 18°, 162°, 162°; 2) 15°, 15°, 165°, 165°; 3) 30°, 30°, 150°, 150°; 4) 10°, 10°, 170°, 170°.

178.

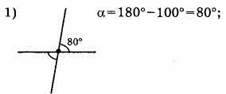
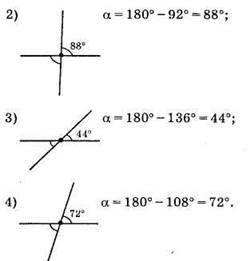
Вертикальні кути

Вертикальні кути

179. 1) Оскільки сума кутів кратна 9 і лежить в межах від 55° до 70°, то ця сума дорівнює 63°. Оскільки вертикальні ку ти рівні, то кожен з них дорівнює 63° : 2 = 31°30′.

2) Оскільки сума кутів кратна 9 і лежить в межах від 111° до 120°, то ця сума дорівнює 117°. Оскільки вертикальні кути рівні, то кожен з них дорівнює 117° : 2 = 58°30′.

3) Оскільки сума кутів кратна 9 і лежить в межах від 241° до 249°, то ця сума дорівнює 243°. Оскільки вертикальні кути рівні, то кожен з них дорівнює 243° : 2 = 121°30′.

Відповідь: 1) 31°30′, 31°30′; 2) 58°30′, 58°30′; 3) 121°30′, 121°30′.

180.

Вертикальні кути

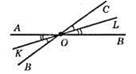
Нехай ∠COB і ∠AОВ – вертикальні, OL – бісектриса ∠COB, ОК – бісектриса ∠AOB. Доведено, що ∠KOL = 180°. Оскільки ∠COB = ∠AOB, то ∠BOL = ∠AOK – як половина рівних кутів. Тоді ∠KOL =∠AOK + ∠AOC + ∠COL = ∠AOC + (∠BOL + ∠COL) = ∠AOC + ∠COB = 180°. Отже, бісектриси вертикальних кутів утворюють розгорнутий кут.

181.

Вертикальні кути

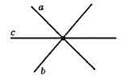
Кількість вертикальних кутів збільшилася на 4 пари, оскільки третя пряма утворює з кожною із даних прямих по 2 пари вертикальних кутів. Всього утворилося 6 пар вертикальних кутів. Кількість суміжних кутів збільшилася на 8 пар, оскільки третя пряма утворює з кожною із даних прямих 4 пари суміжних кутів. Всього утворилося 12 пар суміжних кутів.

Якщо провести четверту пряму, то утвориться 6 + 3 x 2 = 12 вертикальних кутів і 12 + 3 х 4 = 24 суміжних кутів. Якщо провести п’яту пряму, то утвориться 12 + 4 x 2 = 20 вертикальних кутів і 24 + 4 x 4 = 40 суміжних кутів.

182.

Вертикальні кути

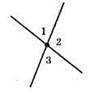
1) ∠1 + ∠2 + ∠3 = 7/6 • 180° = 210°, ∠1 + (∠2 + ∠3) = 210°, ∠1 + 180° = 210°, ∠1 = 210° – 180° = 30°. Отже, прямі перетинаються під кутом 30°.

2) ∠1 + ∠2 + ∠3 = 16/9 • 180° = 320°, ∠1 + (∠2 + ∠3) = 320°, ∠1 + 180° = 320°, ∠1 = 320° – 180° = 140°. Тоді ∠2 = 180° – 140° = 40°. Отже, прямі перетинаються під кутом 40°.

3) ∠1 + ∠2 + ∠3 = 0,25 х 5 х 180° = 225°, ∠1 + (∠2 + ∠3) = 225°, ∠1 + 180° = 225°, ∠1=45°. Отже, прямі перетинаються під кутом 45°.

Вертикальні кути

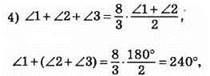
∠1 + 180° = 240°, ∠1 = 240° – 180° = 60°. Отже, прямі перетинаються під кутом 60°.

Відповідь: 1) 30°, 2) 40°, 3) 45°, 4) 60°.

183.

Вертикальні кути

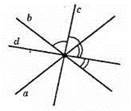
Нехай прямі а і b перетинаються, прямі с і d містять бісектриси двох суміжних кутів. Оскільки бісектриси суміжних кутів утворюють прямий кут, то прямі c i d перетинаються під прямим кутом.

184.

Вертикальні кути

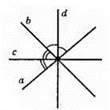
Нехай прямі а і b перетинаються, прямі c i d містять бісектриси утворених вертикальних кутів, а отже містить бісектриси двох суміжних кутів. Оскільки бісектриси двох суміжних кутів утворюють прямий кут, то і прямі c i d перетинаються під прямим кутом.

Застосуйте на практиці

185.

Вертикальні кути

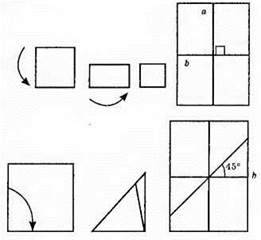
Спочатку слід зігнути аркуш паперу навпіл, а потім ще раз зігнути навпіл. Щоб на згинах отримати дві прямі, що перетинаються під кутом 45°, треба спочатку зігнути аркуш паперу навпіл, потім ще раз зігнути навпіл, а потім зігнути по бісектрисі кута.

186.

Вертикальні кути

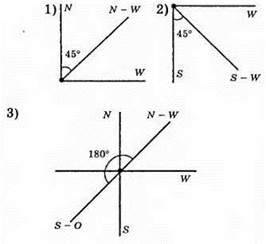
187.

Вертикальні кути

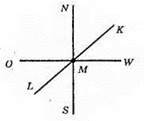
Бісектриса кута між напрямками “північ” і “схід” є промінь МК, бісектриса кута між напрямком “північ” і “захід” є промінь ML. Оскільки кути NMW і OMS – вертикальні, а промені МК і ML – їх бісектриси, то ∠LMK – розгорнутий (бісектриси вертикальних кутів утворюють розгорнутий кут). Отже, бісектриси цих напрямків лежать на одній прямій.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  2. Вертикальні кути. Кут між прямими Урок № 11 Тема. Вертикальні кути. Кут між прямими Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання і доведення теореми про властивість вертикальних кутів; означення кутів між прямими. Сформувати вміння: – будувати вертикальні кути; – знаходити вертикальні кути на рисунку; – розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів. Тип […]...

  3. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  4. Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...

  5. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ Геометрія Евкліда є лише першим кроком до вивчення форм реального простору. О. Смогоржевський РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними […]...

  6. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  7. Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...

  8. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  9. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...

  11. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  12. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  13. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  14. Суміжні кути Урок № 10 Тема. Суміжні кути Мета: домогтися розуміння учнями змісту наслідків з теореми про суму суміжних кутів та змісту понять “наслідок”, “посилання”; використовуючи знання теореми про суміжні кути та її наслідки, виробити вміння розв’язувати задачі на обчислення та доведення, в яких йдеться про суміжні кути. Тип уроку: застосування знань, умінь та навичок. Наочність і […]...

  15. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  16. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  17. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  18. Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...

  19. Тригранні кути 562. Нехай дано тригранний кут, усі плоскі кути якого прямі. Лінійний кут кожного тригранного кута прямий, отже всі його двогранні кути прямі. 563. Якщо всі двогранні кути тригранного кута рівні, то кожний з них більше за 60°, оскільки ∠1 + ∠2 + ∠3 > 180°; ∠Α = ∠1 – ∠2 = ∠3, то 3∠A > […]...

  20. Кути та їх вимірювання Урок № 19 Тема. Кути та їх вимірювання Мета. Формувати уміння та навички будувати кут заданої величини, порівнювати кути, визначати їх градусну міру, користуючись транспортиром, розрізняти на око прямий, тупий та гострий кути. Розвивати окомір, виховувати охайність та старанність. Хід уроку I. Організація класу. II. Перевірка домашнього завдання. 1. Фронтальне опитування А) Що називають кутом? […]...

  21. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  22. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  23. Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...

  24. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  25. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  26. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  27. Кути трикутника і чотирикутника. Розв’язання задач Урок № 51 Тема. Кути трикутника і чотирикутника. Розв’язання задач Мета. Продовжити формування в учнів. вміння розв’язувати задачі геометричного змісту, повторити основні поняття теми, сприяти формуванню практичних навичок при виконанні вправ. Форми роботи: фронтальна бесіда, індивідуальна робота біля дошки, виконання тренувальних вправ, робота з підручником. Обладнання: лінійка, транспортир, кольорова крейда, косинець, таблиці. Тип уроку: урок […]...

  28. Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...

  29. Вимірювання кутів. Види кутів УРОК 36 Тема. Види кутів. Вимірювання кутів Мета: систематизувати знання учнів про поняття кута, його елементів, позначення, вимірювання і класифікацію; вдосконалювати вміння і відпрацьовувати навички вимірювання кутів, визначати видів кутів і розв’язувати задачі на застосування аксіоми вимірювання кутів. Тип уроку: застосовування знань, вмінь та навичок. Обладнання: таблиця “Кути. Вимірювання кутів”. Хід уроку I. Перевірка домашнього […]...

  30. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  31. Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...

  32. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  33. КУТИ ТА ЇХ ВИМІРЮВАННЯ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 5. КУТИ ТА ЇХ ВИМІРЮВАННЯ Подивіться на малюнок 65. Ви бачите дві прямолінійні стежки, що виходять від одного пенька. Стежки нагадують промені, а пеньок – точку, що є спільним початком цих променів. Цей приклад дає уявлення про геометричну фігуру кут (мал. 66). Мал. 65 Мал. 66 Кутом називається […]...

  34. Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого ­кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...

  35. Рівняння. Кути. Трикутники УРОК 42 Тема. Рівняння. Кути. Трикутники Мета: перевірити рівень засвоєння учнями навчального матеріалу; перевірити рівень сформованості вмінь учнів: вимірювати і будувати кути за допомогою транспортира; обчислювати невідомі сторони й периметр трикутника; розв’язувати рівняння з використанням правил знаходження невідомих компонентів дій додавання і, віднімання. Тип уроку: контроль знань. Хід уроку І. Тематична контрольна робота № 3 […]...

  36. КУТИ І ЇХ МІРИ РОЗДІЛ 1 НАЙПРОСТІШІ ГЕОМЕТРИЧНІ ФІГУРИ ТА ЇХ ВЛАСТИВОСТІ & 3. КУТИ І ЇХ МІРИ Два промені, що мають спільний початок, розбивають площину на дві частини. Частину площини, обмежену двома променями із спільним початком, називають кутом. Промені, що обмежують кут, називають сторонами кута, а їх спільний початок – вершиною кута (мал. 30, а). Такий кут називають […]...

  37. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів. Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73). Прямі а і b з їх січною с […]...

  38. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  39. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  40. Кути та їх міри Урок № 18. Тема. Кути та їх міри Мета. Засвоїти поняття кута градусної міри кута, променя, що проходить між сторонами кута; вимірювати кути; записувати кути з малюнка; застосовувати властивості кутів до розв’язання задач, розвивати увагу та допитливість, виховувати інтерес до математики. Обладнання: кодоскоп Хід уроку І. Організація класу ІІ. Перевірка домашнього завдання. Двоє учнів розв’язують […]...

Ви зараз читаєте: Вертикальні кути
«
»