Відстань між двома точками із заданими координатами
УРОК № 24
Тема. Відстань між двома точками із заданими координатами
Мета уроку: виведення формули для знаходження відстані між двома точками, заданими координатами, і застосування формул до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].
Вимоги до рівня підготовки учнів: записують і доводять формулу для знаходження відстані між двома точками, застосовують вивчену формулу до розв’язування задач.
Хід уроку
І. Перевірка домашнього
1. Перевірити наявність виконаних домашніх завдань і відповісти на запитання, які виникли в учнів при виконанні домашніх завдань. 2. Математичний диктант
Сторона квадрата (див. рисунок) дорівнює 5.
Варіант 1
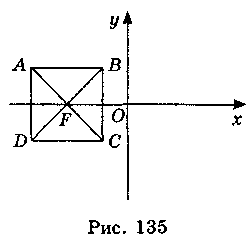
Варіант 2
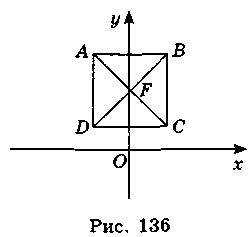
Запишіть координати точок В, С, D, F, середини відрізків AD, АВ, якщо точка А має координати:
Варіант 1 (-6; 2,5);
Варіант 2 (-3; 6).
Відповідь до завдань математичного диктанту
Варіант 1. B(-1;2,5); C(-1;-2,5); D(-6; -2,5); F(-3,5; 0); (-6; 0); (-3,5; 2,5).
Варіант 2. В(3; 6); C(3; l); D(-3; l); F(0; 3,5); (-3; 3,5); (0; 6).
II. Сприйняття
Нехай А(х1; у1), В(х2; у2). Знайдемо відстань між точками А і В.
Розглянемо спочатку випадок х1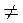 
х2, y1 y2 (рис. 137).
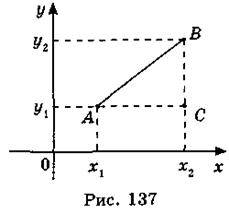
Проведемо AC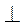
BC. У прямокутному трикутнику ABC маємо:
АС = |х2 – х1|, ВС = |у2 – у1|. За теоремою Піфагора маємо: АВ2 = АС2 + ВС2 або АВ =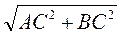 
,
АВ =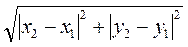 
= 
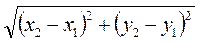. (1)
Якщо у1 = у2 і х1 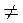х2, то АВ = |х2 – х1|. Такий самий результат у цьому випадку дає і формула (1).
Якщо х1 = х2 і у1 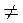у2, то АВ = |y2 – y1|. Такий результат дає і формула (1).
Нарешті, х1 = х2, у1 = у2, тобто якщо точки А і В збігаються, формула (1) дає потрібний результат: АВ = 0.
Отже, як би не були розміщені на координатній площині точки А(х1; у1), В(х2; у2), завжди маємо: АВ = .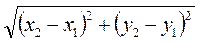
Розв’язування задач
1. Знайдіть відстань між двома точками:
А) А (1) і В (5);
Б) А (-5) і В (-1);
В) А (-3) і В (5);
Г) А(а) і В(b).
2. Знайдіть відстань між двома точками:
А) А (1; 2) і В (4; 6);
Б) А (1; 7) і В (-5; -1);
В) A (a; b) і B (c; d).
III. Закріплення та осмислення нового матеріалу
Розв’язування задач
1. Знайдіть АВ, якщо А(-1; 3), В(3; 0). (Відповідь. АВ = 5) 2. Знайдіть відстань від точки А(-5; 12) до початку координат. (Відповідь. ОА = 13) 3. Знайдіть периметр трикутника ABC, якщо А(-1; 2), В(3; -1), С(-1; -1). (Відповідь. 12) 4. Чи лежать на одній прямій точки А, В, С, якщо:
А) А(1; 4), В(4; 0), С(2; 2);
Б) А(1; 4), В(4; 0), С(2,5; 2)?
(Відповідь, а) Ні; б) так)
5. Яка з точок – А (2; 4) чи В(-3; 2) – лежить ближче до початку координат? (Відповідь. В) 6. Дано точки А (-2; 5), В (1; 8). Знайдіть точку, рівновіддалену від точок А і В, яка лежить:
А) на осі Ох;
Б) осі Оу;
В) відрізку АВ.
(Відповідь, а) (6; 0); б) (0; 6); в) (-0,5; 6,5).)
IV. Домашнє завдання
1. Вивчити формулу для знаходження відстані між двома точками, які задано координатами. 2. Розв’язати задачі. 1) Знайдіть радіус кола, центром якого є точка М(-4; 3), а точка А(-4; 2) лежить на колі. 2) Знайдіть периметр трикутника ABC, якщо А(-1; 3), В(3; 5), С(3; 2).
V. Підбиття підсумків уроку
Запитання до класу
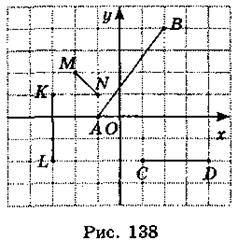
1. Як знайти відстань між двома точками на координатній прямій? 2. Як знайти відстань між двома точками на координатній площині? 3. Знайдіть координати кінців кожного відрізка, зображеного на рис. 138, та обчисліть його довжину.
(1 votes, average: 5.00 out of 5)
Loading...