Головна ⇒ 📌ГДЗ з математики ⇒ Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

Розділ 2. Взаємне розміщення прямих па площині

§ 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с).

2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і січні й с).

Я) ∠2 + ∠3 – 180° (як внутрішні різносторонні кути при паралельних прямих а i b ї січній с).

200. Оскільки m || n, d – січна, то ∠2 + 110° = 180° як сума внутрішніх односторонніх кутів. Звідси ∠2 = 180° – 110° =

70°.

∠1 = 110° (як відповідний кут до кута 110°), ∠3 = ∠1 = 110° (як вертикальні кути).

Відповідь: 110°, 70°, 110°.

201. Оскільки m || n, d – січна, ∠1 = 60° (як відповідний кут до кута 60°).

∠3 = ∠1 = 60° (як вертикальний кут з кутом 60°).

∠2 + ∠1 = 180° (як суміжні кути).

∠2 – 180° – ∠1 = 180° – 60° = 120°.

Відповідь: 60°, 120°, 60°.

202.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

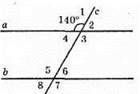
Нехай ∠1 = 140°.

∠3 = ∠1 = 140° (як вертикальні кути).

∠5 = ∠1 = 140° (як відповідні кути).

∠6 = ∠3 = 140° (як вертикальні кути).

∠1 + ∠2 = 180° (як суміжні кути). Звідси ∠2 = 180° – ∠1 = 180° – 140° = 40°.

∠4

= ∠2 = 40° (як вертикальні кути).

∠8 = ∠4 = 40° (як відповідні кути).

∠6 = ∠8 = 40° (як вертикальні кути).

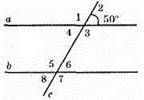
203. Нехай ∠2 = 50°.

∠4 = ∠2 = 50° (як вертикальні кути).

∠4 = ∠8 = 50° (як відповідні кути).

∠6 = ∠8 = 50° (як вертикальні кути).

∠1 + ∠2 = 180° (як суміжні кути). Звідси ∠1 = 180° – ∠2 = 180° – 50° = 130°.

∠3 = ∠1 = 130° (як вертикальні кути).

∠5 = ∠1 = 130° (як відповідні кути).

∠7 = ∠5 = 130° (як вертикальні кути).

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

204. 1) Серед кутів, що утворилися при перетині двох паралельних прямих січною і не є рівними, суміжні і внутрішні односторонні. Однак і ті, й інші кути в сумі дорівнюють 180°.

37° + 133° = 170°. Отже, жоден з решти кутів не може дорівнювати 133°.

2) Так, наприклад, кут, суміжний з кутом 37°, дорівнюватиме 180° – 37° = 143°.

3) Ні, не може, оскільки 37° + 153° = 190° (дивись п. 1).

205.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

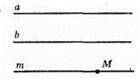
Так, b || m. Оскільки за теоремою про властивість паралельних прямих, якщо а || b, а || m, то b || m.

206.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

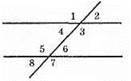
При перетині двох паралельних прямих січною утворилося дві пари внутрішніх різносторонніх кутів: одна пара гострих та одна пара тупих (якщо всі вони не дорівнюють 90°). Оскільки внутрішні різносторонні кути рівні, то кожен з них дорівнює: 240° : 2 = 120°. Це кути ∠3 і ∠5.

Відповідь: 120°.

207. Оскільки відповідні кути, що утворилися при перетині двох паралельних прямих січною, рівні, то кожен з них дорівнює: 108° : 2 = 54°.

Відповідь: 54°.

208. Оскільки ∠1 = ∠2 (внутрішні різносторонні кути), то а || b. Тоді ∠3 і ∠4 – внутрішні односторонні кути при паралельних прямих а і b і січній d. Отже, ∠3 + ∠4 = 1800.

209. Оскільки ∠1 і ∠2 – внутрішні односторонні кути, ∠1 + ∠2 = 180°, то а || b. Тоді ∠3 і ∠4 – внутрішні різносторонні кути при паралельних прямих а і с і січній d. Отже, ∠3 = ∠4.

210.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

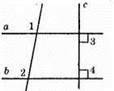
Оскільки ∠1 = ∠2, які є відповідними до ∠4, то а || b. ∠3 і ∠4 – внутрішні односторонні кути при паралельних прямих а i b i січній с. ∠3 + ∠4 – 180°. Звідси ∠4 = 180° – ∠3 = 180° – 90° = 90°. Отже, с ⊥ b.

211.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

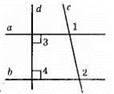
Оскільки a ⊥ d і b ⊥ d, то ∠3 = 90°, ∠4 = 90°. ∠3 і ∠4 – внутрішні односторонні кути при прямих а і b і січній d. ∠3 + ∠4 = 90° + 90° = 180°. Отже, а || b.

∠1 і ∠2 – відповідні кути при паралельних прямих а і b і січній с. Тоді ∠1 = ∠2.

212. 1) Нехай градусна міра одного з внутрішніх односторонніх кутів х, тоді градусна міра другого – х + 16°. Оскільки сума двох внутрішніх односторонніх кутів при паралельних прямих і січній дорівнює 180°, маємо: х + х + 16° = 180°; 2х + 16° = 180°; 2x = 164°; x = 82°. Отже, один з кутів дорівнює 82°, тоді другий – 82° + 16° = 98°.

Відповідь: 82°, 98°.

2) Нехай градусна міра одного з внутрішніх односторонніх кутів дорівнює х, тоді градусна міра другого кута 3х. Оскільки сума двох внутрішніх односторонніх кутів при перетині двох паралельних прямих січною дорівнює 180°, маємо: х + 3х = 180°; 4х = 180°; x = 45°. Отже, один з кутів дорівнює 45°, другий – 45° х 3 = 135°.

Відповідь: 45°, 135°.

3) Нехай градусна міра одного кута дорівнює 5х, тоді другого – 7х.

Оскільки сума двох внутрішніх односторонніх кутів при перетині двох паралельних прямих січною дорівнює 180°, маємо: 5x + 7с = 180°; 12x = 180°; x = 15°. Отже, один з кутів дорівнює 5 x15° = 75°, другий – 7 х 15° = 105°.

Відповідь: 75°, 105°.

213. 1) Нехай градусна міра одного кута дорівнює х, тоді градусна міра другого – 4x.

Оскільки сума двох внутрішніх односторонніх кутів, утворених при перетині двох паралельних прямих січною, дорівнює 180°, маємо: х + 4х = 180°; 5х = 180°; х = 36°. Отже, один з кутів дорівнює 36°, другий – 36° х 4 = 144°.

Відповідь: 36°, 144°.

2) Нехай градусна міра одного кута дорівнює х, тоді другого – х + 8°.

Оскільки сума двох внутрішніх односторонніх кутів, утворених при перетині двох паралельних прямих січною, дорівнює 180°, маємо: х + х + 8° = 180°; 2х = 172°; х = 86°. Отже, один з кутів дорівнює 86°, другий – 86° + 8° = 94°.

Відповідь: 86°, 94°.

3) Сума двох внутрішніх односторонніх кутів, утворених при перетині двох паралельних прямих січною, дорівнює 180°. Позначимо градусну міру одного кута 5х, другого – 4х. 5х + 4х = 180°; 9х = 180°; х = 20°. Отже, один з кутів дорівнює 5 х 20° = 100°, другий – 4 х 20° = 80°.

Відповідь: 100°, 80°.

214. Рис. 155.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

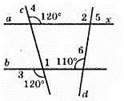
∠1 = ∠3 = 120° (як вертикальні кути). ∠4 = ∠1 = 120° (як відповідні кути). Отже, а || b згідно з ознакою паралельності прямих. ∠2 і ∠6 – відповідні, ∠2 = ∠6 = 110°. ∠5 i ∠2 – суміжні, х + ∠2 = 180°; x + 110° = 180°; х = 180° – 110° = 70°.

Відповідь: 70.

Рис. 156.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

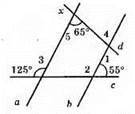
∠1 i ∠2 – суміжні кути. ∠1 + ∠2 = 180°, ∠2 = 180° – ∠1, ∠2 = 180° – 55° = 125°. ∠2 = ∠3 = 125° (як відповідні кути). Отже, а || b згідно з ознакою паралельності прямих.

∠4 і ∠5 – внутрішні різносторонні кути При паралельних прямих а і b і січній d. ∠4 = ∠5 = 65°.

Відповідь: 65°.

Рис. 157.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

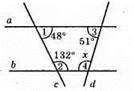
∠1 + ∠2 = 48° + 132° = 180°. Оскільки ці кути внутрішні односторонні і їхня сума дорівнює 180°, то прямі а і b паралельні (наслідок 2).

Розглянемо паралельні прямі а і b і січну d.

∠3 i ∠4 – внутрішні односторонні кути при паралельних прямих а і b і січній d. ∠3 + ∠4 = 180°, ∠4 = 180° – ∠3 = 180° – 51° = 129°.

Відповідь: 129°.

215. Рис. 158.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

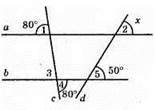
∠3 = ∠4 = 80° (як вертикальні кути).

∠1 = ∠3 (як відповідні кут). Отже, а || b згідно з ознакою паралельності прямих. Розглянемо а || b і січну d. ∠2 = ∠5 як відповідні кути. Отже, х = 50°.

Відповідь: 50°.

Рис. 159.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

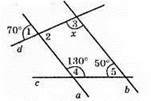
∠4 + ∠5 = 130° + 50° = 180°. Оскільки ці кути внутрішні односторонні та їхня сума дорівнює 180°, то згідно з наслідком 2 прямі а і b паралельні.

Розглянемо а || b і січну d.

∠1 = ∠2 = 70° (як вертикальні кути). ∠2 і ∠3 – внутрішні односторонні кути, отже, ∠2 + ∠3 = 180°. ∠3 = 180° – ∠2 = 180° – 70° = 110°.

Відповідь: 110°.

216.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

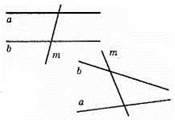
Якщо а і b не паралельні прямій m, то m перетинає а і b.

Якщо пряма перетинає одну з паралельних прямих, то вона перетинає і другу. Тож а і b можуть бути паралельними, або а і b не паралельні і кожну перетинає m.

217.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

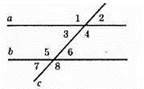
Оскільки сума трьох кутів 120°, то два з цих кутів вертикальні і третій відповідний до одного з них.

∠7 + ∠6 + ∠2 = 120°. Оскільки всі ці кути рівні (∠7 і ∠6 – як вертикальні, ∠2 і ∠6 – як відповідні), то кожен з них дорівнює 40°. ∠2 = 40°, ∠6 = 40°, ∠7 = 40°.

∠3 = ∠2 = 40° (як вертикальні кути).

∠1 + ∠2 = 180° (як суміжні кути). Звідси ∠1 = 180° – 40° = 140°.

∠4 = ∠1 = 140° (як вертикальні кути). ∠5 = ∠1 = 140° (як відповідні кути).

∠8 = ∠5 = 140° (як вертикальні кути).

Відповідь: чотири кути по 40°, чотири кути по 140°.

218.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

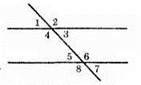
Оскільки сума чотирьох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 128°, то це дві пари відповідних гострих кутів.

∠1 + ∠5 + ∠3 + ∠7 = 128°. Оскільки ці кути рівні, то кожен з них дорівнює 32°.

∠1 = ∠5 = ∠3 = ∠7 = 32°.

∠1 + ∠2 = 180° (як суміжні кути).

∠2 = 180° – ∠1 = 180° – 32° = 148°.

∠4 = ∠2 = 148° (як вертикальні кути).

∠6 = ∠2 = 148° (як відповідні кути).

∠8 = ∠6 = 148° (як вертикальні кути).

Відповідь: чотири кути по 32°, чотири кути по 148°.

219.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

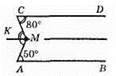
Через т. М проведемо пряму паралельні CD. KM || CD, KM || AB. Тоді ∠CMA = ∠CMK + ∠AMK.

Розглянемо AB || KM і січну AM.

∠AMK = ∠MAB = 50° (як внутрішні різносторонні кути).

Розглянемо CD || KM і січну CM.

∠CMK = ∠DCM = 80° (як внутрішні різносторонні кути).

Отже, ∠CMA = 80° + 50° = 130°.

Відповідь: 130°.

220. Через точку К проведемо пряму KF паралельну MN. KF || MN, KF || PL. Тоді ∠MKP = ∠MKF + ∠PKF.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

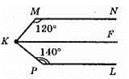
Розглянемо MN || КF i січну МК. ∠MKF + ∠KMN = 180° (як внутрішні односторонні кути). ∠MKF = 180° – ∠KMN = 180° – 120° = 60°.

Розглянемо PL || KF і січну KP. ∠PKF + ∠KPL = 180° (як внутрішні односторонні кути). ∠PKF = 180° – ∠KPL = 180° – 140° = 40°.

Отже, ∠MKP = 60° + 40° = 100°.

Відповідь: 100°.

221.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

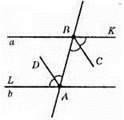
Оскільки а || b, то ∠KBA = ∠BAL (як внутрішні різносторонні). Оскільки ВС і AD – бісектриси цих кутів, то ∠CBA = ∠DAB (як половини рівних кутів). Розглянемо прямі ВС і AD ті січну AB. ∠CBA і∠DAB – внутрішні різносторонні і рівні, отже, ВС || DA.

Отже, бісектриси двох внутрішніх різносторонніх кутів при паралельних прямих і січній паралельні.

222.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

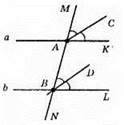
Оскільки а || b, то ∠MAK = ∠ABL (як відповідні кути).

Оскільки АС і BD – бісектриси цих кутів, то ∠ABD = ∠MAC (як половини рівних кутів).

Розглянемо прямі АС і BD і січну MN: ∠MAC і ∠ABD – відповідні кути і рівні. Отже, АС || BD.

Отже, бісектриси двох відповідних кутів при паралельних прямих і січній паралельні.

223.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

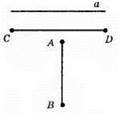
224. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

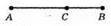
AB = 16 см.

1) ВС = х см, АС = х + 2, х + х + 2 = 16; 2х= 14; х = 7. Отже, ВС = 7, АС = 7 + 2 = 9.

2) ВС = х см, АС = 3х см, х + 3х = 16; 4х = 16; х = 4. Отже, ВС = 4 см, AC = 3 х 4 = 12 см.

3) Нехай АС = 5X, ВС = 3х. 5х + 3х = 16; 8х = 16; х = 2. Отже ВС = 3 x 2 = 6 см, АС = 5 x 2 = 10 см.

4 см

6 см

7 см

9 см

10 см

12 см

Ф

Р

А

Н

К

O

Відповідь: Франко.

225.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

Домашня самостійна робота № 2 (§§ 7-10)

1. Перпендикулярні прямі зображені на рис. 166.

Правильна відповідь Г).

2. Паралельні прямі зображені на рис. 164.

Правильна відповідь Б).

3. На рис. 167 кути 1 і 2 – внутрішні різносторонні.

Правильна відповідь Г).

4. Правильним є твердження Б).

5. Прямі а і b паралельні на рис. 168, оскільки сума внутрішніх односторонніх кутів дорівнює 180° (61° + 119° = 180°).

Правильна відповідь А).

6. Градусна міра одного з інших семи кутів може дорівнювати 145° (це буде кут суміжний до кута 35°).

Правильна відповідь B).

7.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

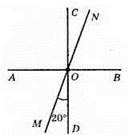
∠CON = ∠MOD = 20° (як вертикальні кути). ∠AON = ∠AOC + ∠CON = 90° + 20°= 110°.

Правильна відповідь В).

8.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

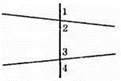
∠1 + ∠2 = 180°, звідси ∠1 = 180° – ∠2.

∠3 + ∠4 = 180°, завіси ∠4 = 180° – ∠3.

∠1 + ∠4 = 180° – ∠2 + 180° – ∠3 = 360° – (∠2 + ∠3) = 360° – 175° = 185°.

Правильна відповідь Б).

9.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

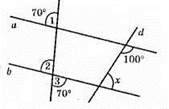
∠2 = ∠3 = 70° (як вертикальні кути).

∠1 = ∠2 = 70° (як відповідні кути). Отже, а || b згідно з ознакою паралельності прямих.

Розглянемо а || b і січну d. Кути 100° і х внутрішні односторонні кути, отже, їхня сума дорівнює 180°. Тоді 100° + х = 180°; х = 80°.

Правильна відповідь А).

10. Правильна відповідь В).

11.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

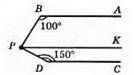
Через т. Р проведемо пряму РК || ВА. Тоді ∠BPD = ∠BPK + ∠DPK.

Розглянемо ВА || РК і січну BP. ∠PBA + ∠BPK = 180° (як внутрішні односторонні кути). ∠BPK = 180° – ∠PBA = 180° – 100° = 80°.

Розглянемо РК || DC і січну PD. ∠DPK + ∠CDP = 180° (як внутрішні односторонні кути) ∠DPK = 180° – ∠CDP = 180°- 150° = 30°.

Отже, ∠BPD = 80° + 30° = 110°.

Правильна відповідь Б).

12. Нехай один із кутів дорівнює х, тоді другий – х + 60°. Суміжні кути відповідно дорівнюють 180° – x і 180° – (x + 60°) = 120° – x.

Складемо пропорцію: 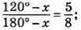Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

960° – 8x = 900° – 5х; 3х = 60°; х = 20°. Отже, менший кут дорівнює 20°.

Правильна відповідь Г).

Завдання для перевірки знань № 2 (§§ 7-10)

1. Паралельні прямі зображені на рис. 178: m || n.

Перпендикулярні прямі зображені на рис. 176: а ⊥ b.

2.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

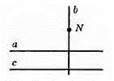
N ∉ а, b ⊥ а, с ⊥ b.

3. 1) 1 і 2 – внутрішні різносторонні кути.

2) 1 і 3 – внутрішні односторонні кути.

3) 1 і 4 – відповідні кути.

4. 1) Прямі KL і МТ не перпендикулярні, оскільки ∠KOA + ∠AOM = 70° + 19° = 89°, а перпендикулярні прямі утворюють кут 90°.

2) Прямі KL і MN перпендикулярні, оскільки ∠KON = ∠KOB + ∠NOB = 121° = 21° = 90.

5.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

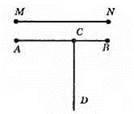
6.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

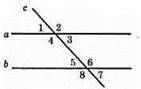
Нехай ∠1 = 78°, тоді ∠3 = ∠1 = 78° (як вертикальні кути), ∠5 = ∠1 = 78° (як відповідні кути), ∠7 = ∠5 = 78° (як вертикальні кути).

∠1 + ∠2 = 180° (як суміжні кути), ∠2 = 180° – ∠1 = 180° – 78° = 102°.

∠4 = ∠2 = 102° (як відповідні кути).

∠6 = ∠2 = 102° (як відповідні кути).

∠8 = ∠6 = 102° (як вертикальні кути).

Відповідь: чотири кути по 78°, чотири кути по 102°.

7.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

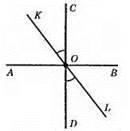
Оскільки AB ⊥ CD, то ∠AOC = 90°. ∠AOK = ∠AOC – ∠KOC, ∠KOC = ∠DOL = 38° (як вертикальні кути). Отже, ∠AOK = 90° – 38° = 52°.

Відповідь: 52°.

8.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

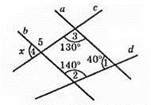
∠1 і ∠2 – внутрішні односторонні кути при прямих а і b і січній d. ∠1 + ∠2 = 40° + 140° = 180°. Згідно з наслідком 2 прямі a i b паралельні.

Розглянемо а || b і січну с. ∠5 = ∠3 = 130° (як внутрішні різносторонні кути).

∠5 + ∠4 = 180° (як суміжні кути). ∠4 = 180° – ∠5 = 180° – 130° = 50°.

Відповідь: 50°.

9.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

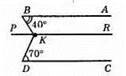
Проведемо пряму PR || DC, тоді ∠BKD = ∠BKP + ∠DKP.

Розглянемо BA || PR i січну BK. ∠BKP = ∠KBA = 40° (як внутрішні різносторонні кути).

Розглянемо KR || DC і січну KD. ∠DKP = ∠KDC = 70° (як внутрішні різносторонні кути).

Отже, ∠BKD = 40° + 70° = 110°.

Відповідь: 110°.

10. Нехай один із внутрішніх односторонніх кутів дорівнює х, тоді другий – 4х. Оскільки їх сума дорівнює 180°, маємо: х + 4х = 180°; 5х = 180°; х = 36°. Отже, один з кутів дорівнює 36°, другий – 4 х 36° = 144°.

Відповідь: 36°, 144°.

11.

Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною

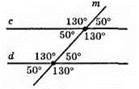
Так, прямі c i d паралельні між собою.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Властивості кутів, утворених при перетині двох паралельних прямих січною Урок № 32 Тема. Властивості кутів, утворених при перетині двох паралельних прямих січною Мета: закріпити знання учнів про зміст та схему доведення теореми про властивості кутів та наслідків з неї; сформувати уявлення учнів про відстань між двома паралельними прямими; сформувати вміння використовувати названі вище теоретичні відомості під час розв’язування задач на знаходження кутів при паралельних […]...

  2. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  3. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  4. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  5. ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 7. ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ ЗАДАЧА Дано пряму а і точку Р, що не належить цій прямій. Проведіть через точку Р пряму, паралельну прямій а. – За допомогою лінійки і косинця побудову можна виконати, як показано на малюнку 90. Чи можна через точку Р провести дві різні прямі, […]...

  6. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  7. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  8. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  9. Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...

  10. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  11. Паралельні прямі. Властивості паралельних прямих Урок № 110 Тема. Паралельні прямі. Властивості паралельних прямих Мета: закріпити знання учнів про властивості паралельних прямих; відпрацювати навички розв’язування задач, що передбачають застосування набутих з теми знань; продовжувати роботу з повторення вивченого у 6 класі матеріалу. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Математичний диктант […]...

  12. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  13. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  14. Властивості паралельних прямих Урок № 8 Тема. Властивості паралельних прямих Мета: домогтися засвоєння учнями змісту таких понять: “теорема”, “доведення теореми”, “умова і висновок теореми”, а також алгоритму доведення методом від супротивного; використовуючи метод доведення “від супротивного”, довести терему про дві прямі, паралельні третій. Сформувати вміння: – відтворювати означення основних понять уроку; – застосовувати названі поняття під час розв’язування […]...

  15. Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...

  16. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів. Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73). Прямі а і b з їх січною с […]...

  17. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  18. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  19. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  20. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  21. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  22. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  23. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  24. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  25. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  26. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  27. Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...

  28. Властивості паралельних площин Урок 18 Тема. Властивості паралельних площин Мета уроку: формування знань учнів про властивості паралельних площин. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування задачі № 24, у цей час клас пише математичний диктант. 2. Математичний диктант. Дано зображення куба: варіант 1 – рис. 64, варіант 2 – рис. 65. […]...

  29. Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...

  30. Види кутів. Вимірювання кутів УРОК 35 Тема. Вимірювання кутів. Види кутів Мета: ознайомити учнів із поняттям порівняння кутів і їх видами залежно від величини кутів; навчити розпізнавати прямі, гострі і тупі кути на рисунку та визначати вид кута за його градусною мірою. Тип уроку: застосування знань, навичок та вмінь. Обладнання: демонстраційний транспортир; таблиця-схема “Кути. Види кутів”, різнокольорові моделі розгорнутого […]...

  31. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  32. Вимірювання кутів. Види кутів УРОК 36 Тема. Види кутів. Вимірювання кутів Мета: систематизувати знання учнів про поняття кута, його елементів, позначення, вимірювання і класифікацію; вдосконалювати вміння і відпрацьовувати навички вимірювання кутів, визначати видів кутів і розв’язувати задачі на застосування аксіоми вимірювання кутів. Тип уроку: застосовування знань, вмінь та навичок. Обладнання: таблиця “Кути. Вимірювання кутів”. Хід уроку I. Перевірка домашнього […]...

  33. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  34. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  35. Ознаки паралельності прямих Урок № 30 Тема. Ознаки паралельності прямих Мета: закріпити знання учнів про ознаки паралельності двох прямих (за кутами, що утворилися при перетині даних прямих січною). Сформувати вміння: – визначати вид двох кутів, що утворилися при перетині двох прямих січною; – за певним співвідношенням цих кутів робити висновок щодо паралельності прямих; – для встановлення співвідношення кутів […]...

  36. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  37. Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...

  38. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  39. Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого ­кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...

  40. Властивості паралельних площин Геометрія Стереометрія Властивості паралельних площин Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка […]...

Ви зараз читаєте: Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною
«
»