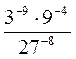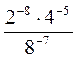Властивості степеня з цілим від’ємним показником
Урок № 26
Тема. Властивості степеня з цілим від’ємним показником
Мета: закріпити знання учнів про означення та властивості степеня з цілим (від’ємним) показником та сформувати вміння використовувати їх для розв’язування вправ на обчислення значень числових виразів та перетворень виразів зі змінними.
Тип уроку: відпрацювання навичок, діагностика засвоєння.
Наочність та обладнання: опорний конспект “Степінь з цілим від’ємним показником”.
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
Для
Для “сильних” учнів пропонуємо індивідуальні завдання на картках.
III. Формулювання мсти і завдань уроку
Проведена перевірка виконання домашнього завдання та аналіз можливих помилок самі по собі створюють мотивацію учнів до діяльності щодо усунення причини помилок (корекції знань), а також удосконалення вмінь. Тому саме корекція знань учнів щодо змісту означення та властивостей степеня з цілим показником та відпрацювання вмінь учнів виконувати перетворення раціональних
IV. Актуалізація опорних знань та вмінь
@ З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: означення і властивості степеня з цілим показником та спосіб застосування для обчислення значень числових виразів, що містять степені з цілим показником, а також для перетворення раціональних виразів, що містять степені з цілим показником.
Виконання усних вправ
1. Подайте вирази у вигляді одночлена: t2 • t5; (т3)2; а7 : а; (ху)5.
2. Спростіть вирази: t -3 • t 6; а 3 : а -2; (а -6) -2; (а -5b -2) -3.
3. Обчисліть значення виразів найзручнішим способом: 2 -13 • 2 25 : 2 12 ; (5 -5) -13 : (5 -16) -4; 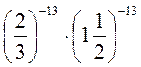 .
.
V. Відпрацювання вмінь
Виконання письмових вправ
@ З метою формування сталих умінь, що згодом перетворяться на сталі навички застосування властивостей степеня з натуральним показником, вправи для письмового розв’язування мають бути складені так, щоб кожна вимагала від учнів застосування всіх 5-ти властивостей степеня. Формулювання самих завдань може повторювати зміст завдань попереднього уроку (звісно, на більш високому рівні складності).
Основну увагу на уроці приділяємо формуванню сталих умінь перетворювати вирази із застосуванням вивчених властивостей степеня. При цьому вчитель може наголосити на тому, що в результаті виконаних дій у відповіді можна дістати степінь із цілим від’ємним показником, при цьому, якщо інакше не сказано в умові, не обов’язково переходити до виразів зі степенями з натуральним показником. Також слід нагадати про те, що, перетворюючи вирази, які містять степені, основи яких – числа, учні повинні намагатися подати компоненти виразів у вигляді степенів з однаковими основами.
Для реалізації дидактичної мети на цьому уроці слід розв’язати завдання такого змісту:
1. Обчислення значень числових виразів (попередньо застосувавши відповідну властивість степеня).
1) Обчисліть:
А) 16-1 • 25 • 42; б) 58 : (125 : 25-1); в) (93 : 3-5) : 27-2; г) 4-5 • 33 • 0,25-5; д) 2-8 • 1,25-8 • 0,4-8; е) 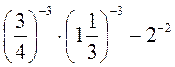 .
.
2) Обчисліть: а) 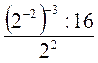 ; б)
; б) 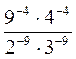 ; в)
; в) 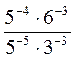 .
.
3) Обчисліть: а) 8 -2 • 43; б) 9 -6 • 275; в) 100 : 10 -3; г) 125 -4 : 25 -5; д) 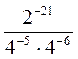 ; є)
; є) 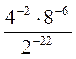 ; ж)
; ж) 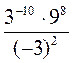 ; з)
; з) 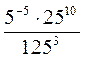 .
.
2. Подання виразу у вигляді степеня з поданою основою (степені або мають однакову основу або потребують переходу до однієї основи).
1) Подайте вираз у вигляді степеня з основою 3 і знайдіть його значення:
А) 27 • 3 -4; б) (3-1)5 • 812; в) 9 -2 : 3-6; г) 813 : (9 -2) -3.
2) Подайте у вигляді степеня з основою 5 вираз, в якому m – ціле:
А) 5m • 5m+1 • 51-m; б) (5m)2 • (5-3)m; в) 625 : 54m – 2.
3. Спрощення виразів.
1) Спростіть вираз:
А) (а -1 – 1)(a -1 + 1) – а -2; б) (b -3 – 3)(b -3 + 3) – b-3(b-3 + 2); в) (x -1 – у -2)2 – (x -1 + y -3)2; г) (с-1 – с)2 – (с-1 – 2с2)(с-1 +2с2); д) (a-1 – b-1)(а-2 + а-1b-1 + b-2); с) 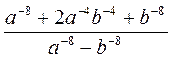 .
.
2) Спростіть вираз:
А) 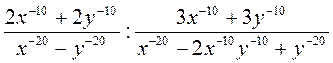 ; б)
; б) 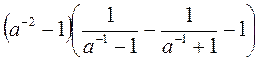 ; в)
; в) 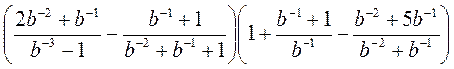 .
.
3) Спростіть вираз:
А) 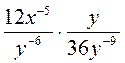 ; б)
; б) 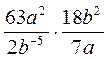 ; в)
; в) 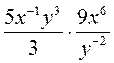 ; г)
; г) 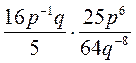 .
.
4) Спростіть вираз: а) 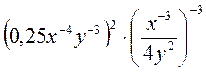 ; б)
; б) 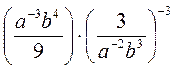 ; в)
; в) 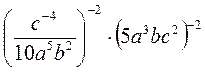 ; г)
; г) 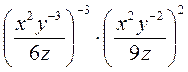 .
.
4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Спростіть вираз: а) 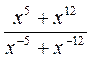 ; б)
; б) 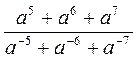 .
.
2) Доведіть, що при будь-якому цілому п рівність є правильною: а) 2n + 2n = 2п+1; б) 2•3n + 3n = 3n+1.
3) Знайдіть пропущений вираз:
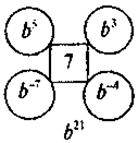
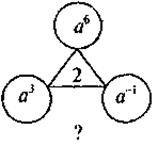
5. На повторення вправи, що передбачають перетворення раціональних виразів.
1) Спростіть вираз:
А) 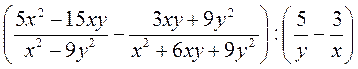 ;
;
Б) 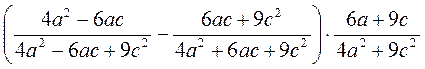 .
.
VI. Підсумки уроку
Самостійна робота № 6
Варіант 1 | Варіант 2 |
1. Виконайте дії: | |
А) 5-1 – 3 • 2-3; б) 2-10 • 26; в) (x – 7)-2; г) | А) 6-1 – 2•3-2; б) 512 • 5-8; в) а-3 : а-6; г) (а-4)3 • а10 |
2. Спростіть вираз: | |
A) 1 | А) 1 |
3. Обчисліть: | |
|
|
VII. Домашнє завдання
1. Повторити зміст означення та властивостей степеня з цілим від’ємним показником.
2. Виконати вправи іншого варіанта самостійної роботи (провести аналіз помилок за розданими розв’язаннями).
3. Повторити правила виконання множення і ділення числа на розрядну одиницю (довідник, 5 клас).
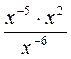 .
.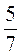 X6у -10 • 0,7x-4у2; г)
X6у -10 • 0,7x-4у2; г) 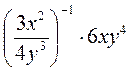 .
.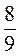 А7b-12 • 0,9a-5b13; б)
А7b-12 • 0,9a-5b13; б) 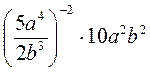 .
.