Вступ. Точка і пряма. Властивості точок і прямих
Урок № 1
Тема. Вступ. Точка і пряма. Властивості точок і прямих
Мета: ознайомити учнiв з предметом вивчення геометрiї, планiметрiї та iз поняттям найпростiших фiгур у геометрiї, домагатися вiд учнів свiдомого засвоєння термiнологiї, що описує взаємне розташування точок та прямих на площинi, формулювання основних властивостей розташування точок та прямих; виробити первиннi вмiння позначати точки та прямi на рисунку, описувати ситуацiю, що зображена на рисунку та, навпаки, за описом ситуацiї виконувати вiдповiднi рисунки, користуючись найпростiшим
Тип уроку: засвоєння знань, умiнь та навичок.
Форма проведення: бесiда.
Наочнiсть та обладнання: демонстрацiйні креслярськi iнструменти.
ХIД УРОКУ
І. Органiзацiйний момент
Учитель повiдомляє учнів про органiзацiю навчального процесу з вивчення геометрiї, знайомить з вимогами програми щодо знань та вмінь (в адаптованiй формi), пояснює структуру пiдручника, його особливостi.
ІІ. Формулювання мети й завдань уроку
Виходячи з теми уроку та погодження її з учнями, вчитель формулює основну дидактичну мету уроку (див. вище).
ІІІ. Засвоєння нових знань
План вивчення
1°. Вступна бесiда.
А) Зародження геометрiї;
Б) геометрiя Евклiда;
В) з iсторiї розвитку геометрiї, будова геометрiї;
Г) найпростiшi геометричнi фiгури;
Д) що таке аксiома.
2°. Точка i пряма.
3°. Властивостi точок i прямих.
А) Властивiсть належностi точок i прямих;
Б) аксiома проведення прямої;
В) аксiома розмiщення точок на прямiй.
Методичний коментар
1°. Додатковий матерiал для вступної бесiди про розвиток геометрiї можна взяти з книг: Глейзер Г. И. История математики в школе.- М.: Просвещение, 1982, 1983; Большая советская энциклопедия.- М.: Советская энциклопедия, 1971.- Т. 6.- С. 307.
У вступнiй бесiдi можна використати геометричнi знання, яких учні набули в 1-6 класах, та звернутися до їх життєвого досвiду.
2°. Пiд час викладення цього питання слiд нагадати учням, як зображується пряма та точки, їх позначення (слiд указати на те, що для розрiзнення тепер зазвичай пряму будемо позначати однiєю маленькою латинською лiтерою, а точки – великими латинськими лiтерами).
3°. Новi термiни “лежить”, “не належить”, “проходить через точку”, “перетинаються”, “лежить мiж” тощо, слiд уводити одночасно з виконанням рисунка.
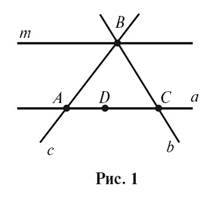
При цьому, увiвши поняття, вчитель формулює аксiому проведення прямої та аксiому розмiщення точок на прямiй. Пiд час пояснення можна використовувати рисунок 1.
IV. Первинне усвiдомлення нових знань
Для засвоєння введеної термiнологiї та аксiом можна виконати уснi вправи.
Виконання усних вправ
1. На прямiй AB позначено точку C. Чи лежить точка A на прямiй BC? Чи лежить точка B на прямiй AC?
2. Точка A лежить на прямiй c, а точка B не лежить на прямiй c. Чи перетинаються прямi c i AB? Якщо так, то назвiть точку їхнього перетину.
3. Через точку A проведено двi прямi. Чи можуть цi прямi мати спільну точку B, вiдмiнну вiд точки A?
4. Точка B лежить на прямiй мiж точками A i C. Як розмiщенi точки B i C вiдносно точки A?
5. На прямiй позначено точки K, L, M, N (рис. 2).
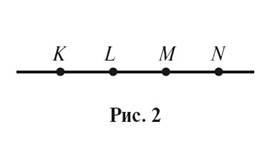
Назвiть:
А) точку, що лежить мiж точками L i N;
Б) точки, що лежать мiж точками K i N;
В) двi точки, що лежать по один бiк вiд точки L;
Г) точку, по рiзнi боки вiд якої лежать точки K i M.
6. Розгляньте рисунок 1 i дайте вiдповiдь на запитання.
А) На яких прямих лежить точка A? точка B? точка C? точка D?
Б) Якi прямi проходять через точки: A; B; C; D?
В) В якiй точцi перетинаються прямi a i b; b i c; c i m; b i m?
Г) В якiй точцi перетинаються три прямi? Назвiть цi прямi.
Д) Яка точка на рисунку лежить мiж двома iншими? Чи можна сказати, що точка A лежить мiж точками B i D?
Виконання графiчних вправ
Проведiть пряму.
А) Позначте точки A i B, що лежать на цiй прямiй, i точки C i D, що не лежать на нiй. Як можна назвати цю пряму?
Б) Проведiть ще одну пряму через точки A i C. Скiльки спiльних точок мають побудованi прямi?
Виконання письмових вправ
Рiвень А
1. Позначте точки B i C. Проведiть через них пряму. Проведiть ще одну пряму так, щоб вона проходила через точку B, але не проходила через точку C. Скiльки спiльних точок мають цi прямi?
2. На прямiй точки E i F лежать по рiзнi боки вiд точки D. Як розмiщенi точки D i F вiдносно точки E? Чи може точка F лежати мiж точками D i E?
Рiвень Б
1. Дано чотири точки, причому жоднi три з них не лежать на однiй прямiй. Через кожнi двi з даних точок проведено пряму. Скiльки всього прямих проведено?
2. На прямiй точка B лежить мiж точками A i C. Позначте на цiй прямiй точку D, що лежить мiж точками B i C. Назвiть точку, що лежить мiж точками A i D. Якi з позначених точок лежать по один бiк вiд точки C?
Рiвень В
Скiльки прямих можуть визначити чотири точки? Розгляньте всi можливi випадки. Зробiть рисунки.
Методичний коментар
Необхiдно з перших урокiв пiд час розв’язування вправ рiзного рівня складностi привчати учнiв до попереднього здiйснення певних послiдовних мiркувань, що грунтуються на змiстi розглянутих понять та на аксiомах.
Наприклад
Позначте точки B i C. Проведiть через них пряму. Проведiть ще одну пряму так, щоб вона проходила через точку B, але не проходила через точку C. Скiльки спiльних точок мають цi прямi?
Розв’язання. Позначимо точки B i C. За аксiомою проведення прямої, через цi двi точки можна провести пряму i тiльки одну (рис. 3).
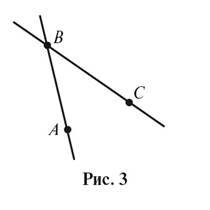
Вiзьмемо точку A, що не лежить на прямiй BC. Тодi через точки A i B, за аксiомою проведення прямої, можна провести пряму AB, до того тiльки одну.
Отже, прямi AB i BC мають одну спільну точку B.
V. Пiдсумки уроку
Диктант
1. Проведiть пряму, використавши аксiому проведення прямої, позначте її.
2. Проведiть пряму a, позначте точку C, яка лежить на прямiй a, точку D, що не лежить на прямiй a. Проведiть пряму b, що проходить через точку D i перетинає пряму a. Позначте точку перетину прямих лiтерою F.
3. Позначте на прямiй a точки M, S i K так, щоб точка K лежала мiж точками M i S. Позначте на прямiй точку A, щоб точки S i K лежали по один бiк, а точка M – по iнший бiк вiд точки A. Прочитайте назви точок за порядком, починаючи з точки M. Запишiть утворене слово.
VI. Домашнє завдання
1. Позначте двi точки й вiд руки проведiть через них пряму. Перевiрте правильнiсть побудови за допомогою лiнiйки. Якою аксiомою ви скористалися?
2. Точки M i N лежать на прямiй по один бiк вiд точки K. Яка з цих трьох точок не може лежати мiж двома iншими? Вiдповiдь обгрунтуйте.
3. Точки A, B, C лежать на однiй прямiй, а точка D не лежить на цiй прямiй. Через кожнi двi з даних точок проведено пряму. Скiльки всього прямих проведено?
4. На прямiй позначено точки X, Y, Z, причому точки X i Y лежать по один бiк вiд точки Z, а точки X i Z – по один бiк вiд точки Y. Яка з трьох точок лежить мiж двома iншими?
Додаткова задача
Скiльки рiзних прямих можуть задавати точки:
А) A, B, C;
Б) A, B, C, D;
В) A, B, C, D, O?
Вiдповiдь пояснiсть, проiлюструвавши її рисунками.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.