Головна ⇒ 📌ГДЗ з математики ⇒ Взаємне розміщення двох кіл

Взаємне розміщення двох кіл

Розділ 4. Коло і круг. Геометричні побудови

§ 25. Взаємне розміщення двох кіл

656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок.

657. 1)

Взаємне розміщення двох кіл

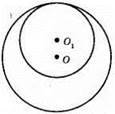
Кола мають внутрішній дотик.

2)

Взаємне розміщення двох кіл

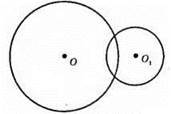
Кола перетинаються.

3)

Взаємне розміщення двох кіл

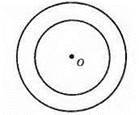
Кола концентричні.

658. 1)

Взаємне розміщення двох кіл

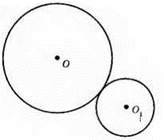
Кола мають зовнішній дотик.

2)

Взаємне розміщення двох кіл

Кола не перетинаються.

659.

Взаємне розміщення двох кіл

АВ = 4 см.

Кола дотикаються (зовнішній дотик).

660.

Взаємне розміщення двох кіл

AB = 2 см. Кола мають внутрішній дотик.

661. 1)

Взаємне розміщення двох кіл

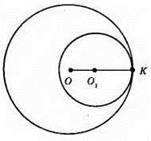
ОК = 7 см, О1К = 5 см.

OO1 = OK – O1К = 7 см – 5 см = 2 см.

2) ОМ = 7 см, О1М = 5 см, ОО1 = ОМ + О1М = 7 см + 5 см = 12 см.

Взаємне розміщення двох кіл

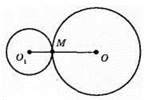
662. 1)

Взаємне розміщення двох кіл

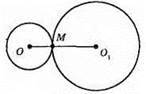
ОМ = 3 см, О1М = 8 см.

OO1 = О1M + ОМ = 8 см + 3 см = 11 см.

2)

Взаємне розміщення двох кіл

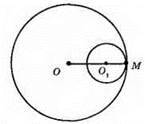
ОМ = 8 см, О1M = 3 см, OO1 = ОM – О1M = 8 см – 3 см = 5 см.

663.

Взаємне розміщення двох кіл

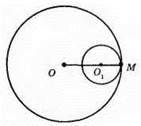
OO1 = 12 см, О1M : ОМ = 2 : 5.

Нехай О1M = 2х, OM = 5x, тоді OO1 = 5x – 2x = 3x; 3x = 12; x = 12 : 3 = 4. Отже, О1M = 2 x 4 = 8 (см), ОМ = 5 х 4 = 20 (см).

Відповідь: 20 см,

8 см.

664.

Взаємне розміщення двох кіл

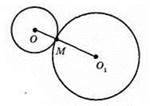
Нехай ОМ = 2x, O1M = 3x. OO1 = OM + О1M = 2x + 3х = 5x. За умовою OO1 = 15 см. Отже, 5x = 15; x = 3. OM = 2 x 3 = 6 (см), О1M = 3 x 3 = 9 (см).

Відповідь: 6 см, 9 см.

665. Позначимо відстань між центрами кіл О1О2, радіуси кіл r1 і r2.

1) Оскільки 9 см + 3 см = 12 см, тобто О1О2 = r1 + r2, то кола дотикаються (зовнішній дотик кіл).

2) Оскільки 5 + 2 < 12, тобто О1О2 > r1 + r2, то кола не перетинаються.

3) Оскільки 13 см – 1 см = 12 см, тобто О1О2 = r1 – r2, то кола дотикаються (внутрішній дотик).

4) 9 см – 7 см < 12 см < 9 см + 7 см, тобто r1 – r2 < О1О2 < r1 + r2, то кола перетинаються.

666. Позначимо відстань між центрами кіл О1О2, а радіуси кіл r1 і r2.

1) 7 см + 5 см < 14 см, тобто О1О2 > r1 + r2. Отже, кола не перетинаються.

2) 16 см – 2 см = 14 см, тобто О1О2 = r1 – r2. Отже, кола мають внутрішній дотик.

3) 10 см – 5 см < 14 см < 10 см + 5 см, тобто r1 – r2 < О1О2 < r1 + r2. Отже, кола перетинаються.

4) 7 см + 7 см = 14 см, тобто О1О2 = r1 + г2. Отже, кола мають зовнішній дотик.

667.

Взаємне розміщення двох кіл

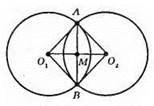
?AО1О2 = ?ВО1О2 (за трьома сторонами (О1А = O1B – як радіуси, О2А = O2B – як радіуси, O1O2 – спільна сторона).

З рівності трикутників маємо: ∠AO1O2 = ∠BO1O2. ?АО1В – рівнобедрений, оскільки О1А = О1В, O1М – бісектриса, отже, O1M – висота, тобто O1М ⊥ AB, а звідси O1O2⊥ AB (так як O1O2 міститьO1М).

668.

Взаємне розміщення двох кіл

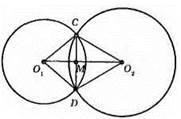
?CO1O2 = ?DO1O2 (за трьома сторонами: O1C = O1D – як радіуси, O2C = O2D – як радіуси, O1O2 – спільна сторона).

З рівності трикутників випливає, що ∠CO1O2 = ∠DO1O2, тобто O1O2 – бісектриса кута CO1D.

669.

Взаємне розміщення двох кіл

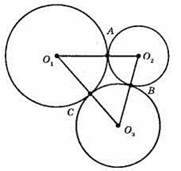
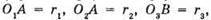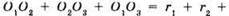
Нехай O1O2 = 5 см, O2O3 = 7 см, O1O3 = 8 см. Нехай Взаємне розміщення двох кіл тоді Взаємне розміщення двох кілВзаємне розміщення двох кіл Тоді

Взаємне розміщення двох кіл

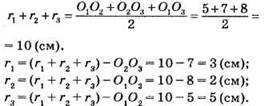
Відповідь: 3 см, 2 см, 5 см.

670.

Взаємне розміщення двох кіл

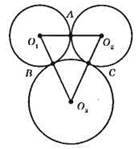
Нехай O1O2 = 14 см, O3В = O3С = 6 см.

Взаємне розміщення двох кіл

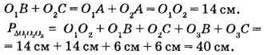
Відповідь: 40 см.

671.

Взаємне розміщення двох кіл

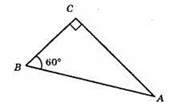
Нехай? ABC – прямокутний (∠C = 90°), ∠B = 60°, AB = 20 см.

За властивістю суми кутів прямокутного трикутника ∠B + ∠A = 90°, звідси ∠A = 90° – ∠B = 90° – 60° = 30°.

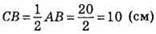Взаємне розміщення двох кіл (за властивістю прямокутного трикутника з кутом 30°).

Відповідь: 10 см.

672.

Взаємне розміщення двох кіл

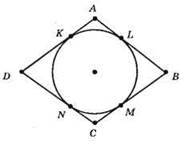
Нехай К, L, М, N – точки дотику. Тоді за властивістю відрізків дотичних, проведених з однієї точки до кола, маємо: AK = AL, BL = ВМ, CM = CN, DN = DK. Додавши почленно чотири останні рівності, маємо: АК + ВМ + CM + DK = AL + BL + CN + DN; (AK + DK) + (ВМ + CM) = (AL + BL) + (CN + DN); AD + ВС = AB + CD.

673.

Взаємне розміщення двох кіл

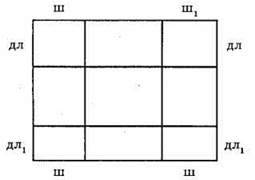
2(ш + дл) = 12; ш + дл = 6; (1)

2(ш + дл) = 13; ш1 + дл = 6,5; (2)

2(ш + дл1) = 16; ш + дл1 = 8. (3)

Отримаємо: ш1 – ш = 0,5. Додамо отримане рівняння з третім рівнянням, отримаємо ш + дл1 = 0,5 + 8 = 8,5.

Отже, периметр зафарбованого прямокутника дорівнює 2 х 8,5 = 17 (см).

Відповідь: 17 см.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (2 votes, average: 3.00 out of 5)
Loading...


Related posts:

  1. Взаємне розміщення двох кіл на площині – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення двох кіл на площині D = О1, O2 – відстань між центрами кіл. R, r – радіуси кіл. D < R – r – кола не мають спільних точок. D = R – r – внутрішній дотик кіл, кола мають одну спільну точку. R – r < d […]...

  2. Взаємне розміщення двох прямих у просторі Урок 7 Тема. Взаємне розміщення двох прямих у просторі Мета уроку: вивчення взаємного розташування двох прямих у просторі: прямі, що перетинаються; паралельні прямі; мимобіжні прямі. Формування понять: паралельні прямі, мимобіжні прямі. Обладнання: стереометричний набір, каркасна модель куба, схема “Взаємне розміщення двох прямих у просторі”. Перевірку правильності виконання домашньої задачі провести шляхом фронтальної бесіди за записами, […]...

  3. Взаємне розміщення кола і прямої – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення кола і прямої Коло і пряма не мають спільних точок. Коло і пряма мають одну спільну точку. А – дотична А – точка дотику Коло і пряма мають дві спільні точки. А – січна Рівняння кола (х – а)2 + (y – b)2 = R2, де (а, b) […]...

  4. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...

  5. Взаємне розміщення прямих у просторі УРОК № 52 Тема. Взаємне розміщення прямих у просторі Мета уроку: повторити, привести в систему й розширити відомості про взаємне розміщення двох прямих у просторі. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]. Вимоги до рівня підготовки учнів: описують взаємне розміщення в просторі двох прямих; застосовують вивчені означення та властивості до розв’язування […]...

  6. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  7. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  8. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Урок 15 Тема. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Мета уроку: формування знань учнів про взаємне розміщення двох площин у просторі. Вивчення ознаки паралельності двох площин. Обладнання: стереометричний набір, схема “Взаємне розміщення двох площин”. Хід уроку 1. Перевірити наявність виконаних завдань та відповісти на запитан­ня, які виникли в учнів під час […]...

  9. Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...

  10. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  11. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  12. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  13. Система двох лінійних рівнянь із двома змінними (1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню; (2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню. 1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3). 1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5. 2 розв’язки до першого […]...

  14. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  15. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  16. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  17. ВСТУП. АКТУАЛІЗАЦІЯ ЗНАНЬ УЧНІВ, СФОРМОВАНИХ У ДОШКІЛЬНИЙ ПЕРІОД. ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЕДМЕТІВ У ПРОСТОРІ І НА ПЛОЩИНІ. ПІДГОТОВЧІ ВПРАВИ ДО НАПИСАННЯ ЦИФР ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 1. ВСТУП. АКТУАЛІЗАЦІЯ ЗНАНЬ УЧНІВ, СФОРМОВАНИХ У ДОШКІЛЬНИЙ ПЕРІОД. ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЕДМЕТІВ У ПРОСТОРІ І НА ПЛОЩИНІ. ПІДГОТОВЧІ ВПРАВИ ДО НАПИСАННЯ ЦИФР Мета: познайомити дітей з предметом математика; закріпити уявлення про розташування предметів на площині та в просторі з використанням слів […]...

  18. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  19. Властивість відрізків дотичних [Дотик двох кіл) Урок № 44 Тема. Властивість відрізків дотичних [Дотик двох кіл] Мета: вивчити властивість відрізків дотичних та схему доведення [засвоїти зміст поняття “дотик двох кіл” та видів дотику двох кіл і залежність між відстанню і центрами двох кіл та радіусами кіл у випадках внутрішнього та зовнішнього дотику]. Сформувати вміння: – відтворювати властивості дотичних та описувати взаємне […]...

  20. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  21. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  22. Різниця квадратів двох виразів 533. a2 – 144 = (a – 12)(a + 12). 534. -49 + b2 = b2 – 49 = b2 – 72 = (b – 7)(b + 7). 535. 1) а2 – 9 = а2 – 32 = (а – 3)(а + 3); 2) b2 + 1 – не можна розкласти на множники; 3) 4 […]...

  23. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

  24. Добуток різниці та суми двох виразів Рівняння коренів не має; Коренем рівняння є будь-яке число; Отже, значення виразу не залежить від значення змінної. 2) (2a – b)(2a + b) + (b – с)(b + с) + (с – 2а)(с + 2а) = 4а2 – b2 + b2 – с2 + с2 – 4а2 = 0. Отже, значення виразу не залежить від […]...

  25. Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...

  26. Вписана та описана сфера 1. Нехай О А – радіус кулі, ОА = 1 см. АВ = ΚΚ1 = 2ОА = 2 см. CD = 2СО = 2 см. Sбіч. = PKLMN× КК1 = 4 × 2 × 2 = 16 (см2). Відповідь: 16 см2. 2. Нехай АВ =AD = ВВ1 = а. З ΔABD: З ΔΒ1BD: В1D2 = […]...

  27. Сума й різниця кубів двох виразів 682. 1) Якщо b = -2, то (1 – b2)(1 + b2 + b4) = 1 – (b2)3 = 1 – b6 = 1 – (-2)6 = 1 – 64 = -63. 2) Якщо х = -1, то 2х3 + 7 – (х + 1)(х2 – х + 1) = 2х3 + 7 – (х3 […]...

  28. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  29. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  30. Квадрат суми та квадрат різниці двох виразів 567. (5а + 3)2 = 25а2 + 30а + 9. 568. Тотожності: 3) (12а – b)2= 144а2 – 24аb + b2. Рівняння коренів не має. 577. (a – b)2 = (b – a)2 – тотожність, бо (a – b)2 = a2 – 2ab + b2; (b – a)2 = b2 – 2ab + a2, a […]...

  31. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  32. Куля і сфера 1028. Нехай OA и OB – радіуси кулі з центром в точці О, OA = OB = 50 см, AB = 80 см. Проведемо OD + AB. ΔAOB – рівнобедрений (OA = OB — як радіуси кулі). OD – висота, а також медіана. Отже, AD = DB = 80 : 2 = 40 (см). З […]...

  33. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  34. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  35. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  36. Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...

  37. Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...

  38. Об’єми кулі та її частини. Площа сфери 1. Обчислимо площу поверхні Землі: S= 4πR2 = 4π · 63752. Площа суші складає Відповідь: π × 63752. 2. Знайдемо об’єм кавуна радіуса 10 см: На одного їдока приходиться Знайдемо об’єм кавуна-радіусом 20 см: На одного їдока приходиться Відповідь: у вісьмох. 3. Оскільки передбачається, що каша у двох котлах однакова, То в другому казані відношення […]...

  39. Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...

  40. Розміщення цінних паперів часткове Фінансовий ринок СЛОВНИК ФІНАНСОВИХ ТЕРМІНІВ Розміщення цінних паперів часткове – розміщення цінних паперів серед обмеженого кола фізичних і юридичних осіб без публікації проспекту емісії....

Ви зараз читаєте: Взаємне розміщення двох кіл
«
»