Застосування координат
124.
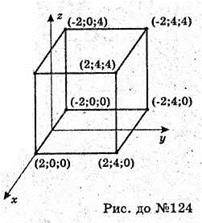
Б) 0 ≤ x ≤ 4; 0 ≤ у ≤ 4; 0 ≤ z ≤ 4.
125.
0 ≤ х ≤ 3; 0 ≤ у ≤ 3; -3 ≤ 2 ≤ 3.
126.
А) А(0; 0; 0); В(0; 1; 0); С(1; 1; 0); D(1; 0; 0);
А1(0; 0; 1); В1(0; 1; 1); С1(1; 1; 1); D(1; 0; 1);
Б) А(0,5; -0,5; 0); В(0,5; 0,5; 0); С(-0,5; 0,5; 0); D(-0,5; 0,5; 0);
А1(0,5; -0,5; 1); В1(0,5; 0,5; 1); С1(-0,5; 0,5; 1); D1(-0,5; -0,5; 1);
В) 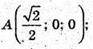
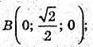
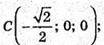
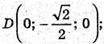
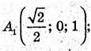
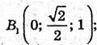
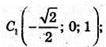
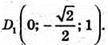
127.
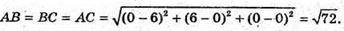
Нехай D(x; у; z, тоді 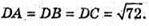
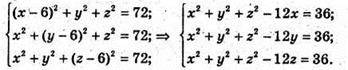
Звідси х = у = z. Тоді (х – 6)2 + х2 + х2 = 72; 3×2 – 12x – 36 = 0;
X2 – 4х – 12 = 0; х1 = 6; х2 = -2. .
Отже, D(6; 6; 6) або D(-2;-2;-2).
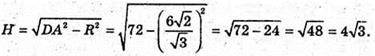
128.
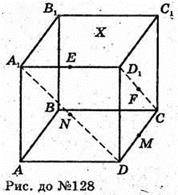
E – середина A1D1; F – середина D1C, тоді EF – середня лінія ΔA1D1C,
Тоді EF? А1С і 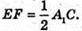
N – середина A1D1, М – середина DC, NM – середня лінія ΔA1DC,
Тому MN? А1С і 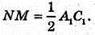
Звідси EF? NM і EF = NM. Тому EFMN – паралелограм.
Отже, ЕМ і NF перетинаються і точкою перетину діляться навпіл
(властивість діагоналей паралелограма).
129.
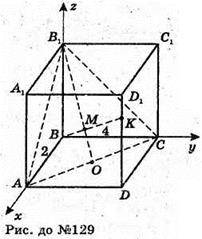
Розмістимо паралелепіпед в системі координат таким чином:
В – в початок координат, ВА лежить на осі х; ВС – на у, ВВ1 на осі z.
Тоді В1(0; 0; 6), В(0; 0; 0), К(2; 4; 3), O(1; 2; 0).
О – точка перетину діагоналей основи ABCD.
Відрізок ВК перетне площину AB1C в точці М, що належить відрізку ВО.
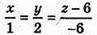 – рівняння B1O; z – 6 = -6х; z = – 6х + 6;
– рівняння B1O; z – 6 = -6х; z = – 6х + 6;
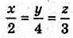 – рівняння ВК;
– рівняння ВК; 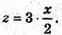
Звідси 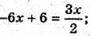
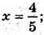
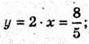
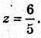
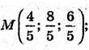
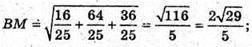
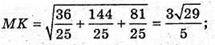
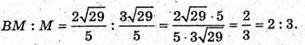
130.
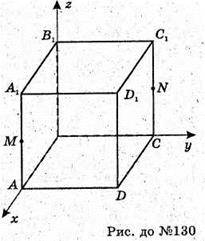
Розмістимо прямокутну систему координат відносно даного куба,
Як показано на рисунку і позначимо АВ = 1, тоді: B1(0; 0; 1);
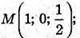
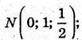 D(1; 1; 0).
D(1; 1; 0).
Складемо рівняння площини (В1MN).
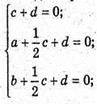
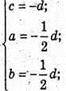
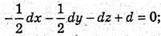
X + y + 2z – 2 = 0 – рівняння площини (B1NM).
Перевіримо чи належить т. D(1; 1; 0) даній площині:
1 + 1 + 2 × 0 – 2 = 0 – вірно, отже, площина (В1MN) проходить через т. D.
Б) AM : МА1 = 3 : 1, тоді 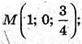 CN : NC1 =1 : 3, тоді
CN : NC1 =1 : 3, тоді 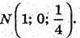
Рівняння площини (B1MN):
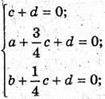
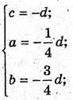
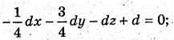
Х + 3у + 4z – 4 = 0 – рівняння площини (B1MN).
Т. D(1; 1; 0) належить площині (B1MN), бо 1 + 3 × 1 + 4 × 0 – 4 = 0 – вірно.
131.
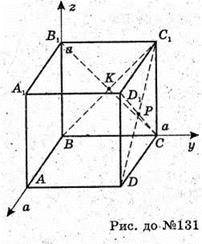
Розташуємо куб в системі координат як показано на рисунку.
Р – центр грані DD1C1C.
R – центр грані BB1C1C. Ребро куба дорівнює а.
Тому А(0; 0; 0); А1(а; 0; а); 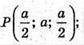
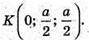
0(х; у; z) – центр сфери. Тоді ОА = ОА1 = ОK = ОР і ОА2 = ОА12 = ОK2 = ОР2
Або 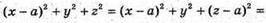
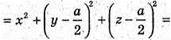
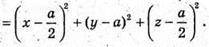
Маємо систему:
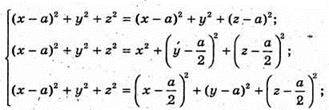
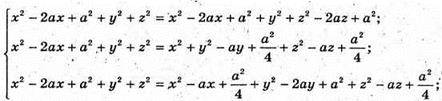
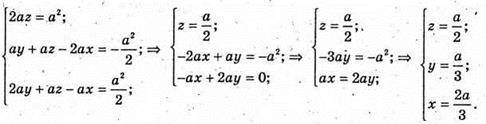
Отже, 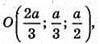 Тоді
Тоді 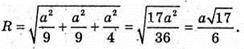
132.
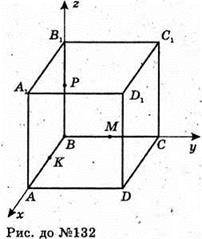
Розмістимо куб в координатній системі, як показано на рисунку.
Сфера проходить через точку В, М – середина ВС, K – середина BA,
Р – середина ВВ1. Якщо ребро куба дорівнює а, то В(0; 0; 0); 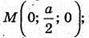
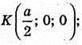
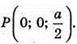
О – центр сфери; O(х; у, z), тоді ОB = ОМ = ОK = ОР і ОВ2 = ОМ2 = ОK2 = ОР2.
Маємо систему:
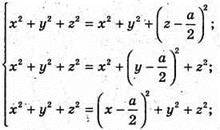
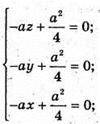
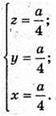
Отже, 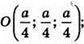
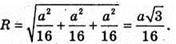
133.
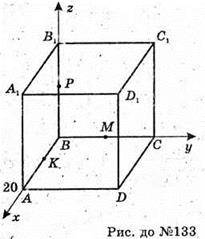
Розмістимо куб в координатній системі, як показано на рисунку.
Сфера проходить через середини ребер BA, ВС, ВВ1, тобто через точки
K, Μ, Р і вершину D1. Ребро куба 20.
Тому K(10; 0; 0), М(0; 10; 0), Р(0; 0; 10), D,(20; 20; 20).
O(х; у; z) – центр сфери.
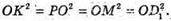
Маємо систему:
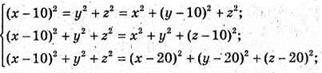
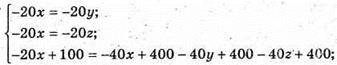
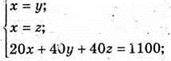
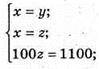
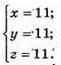
Отже, O(11; 11; 11);
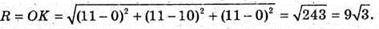
134.
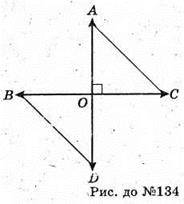
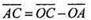
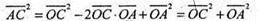 Або АС2 =ОС2+ОА2 (і)
Або АС2 =ОС2+ОА2 (і)
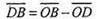
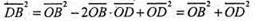 Або DB2 = OB2 + OD2(ІІ)
Або DB2 = OB2 + OD2(ІІ)
Додамо почленно рівності І і II.
АС2 + DB2 = ОС2 + ОА2 + ОВ2 +OD2 = (ОС2 + OD2) + (OA2 + ОВ2) = DC2 + АВ2.
Отже, AC2 + DB2 = DC2 + AB2.
135.
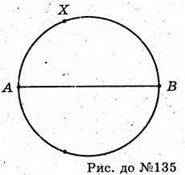
Побудуємо коло, діаметром якого є даний відрізок, тоді кожна точка X кола має таку властивість: АХ2 + ХВ2 = АВ2, тобто сума квадратів відстаней від точок кола до кінців відрізка стала величина. Точки фігури, яку одержимо обертанням кода навколо свого діаметра АВ, мають цю властивість: сума квадратів відстаней від цих точок до кінців відрізка є величиною сталою. Ця фігура – сфера з діаметром АВ.
136.
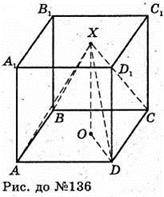
X – довільна точка грані A1B1C1D1
ХА2 + ХВ2 + ХС2 + XD2 буде найменшою, якщо X – точка перетину діагоналей грані A1B1C1D1
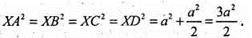
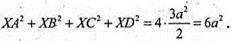
137.
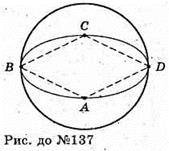
X – довільна точка сфери. Якщо провести площину (ХАС), то площина пройде через т. О. ∠ХАС = 90°, вписаний, спирається на діаметр СА. Тоді за теоремою Піфагора ХС2 + ХА2 = СА2, аналогічно ХВ2 + XD1 = BD2.
Тоді ХС2 + ХА2 +XB2 + XD2 = CA2 + DB2, тобто ХС2 + ХА2 + ХВ2 + XD2 – стала величина, незалежно від вибору т. X.
138.
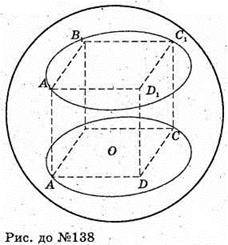
X – довільна точка сфери.
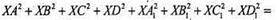
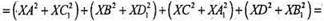
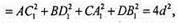
Де d – діагональ куба. Отже, незалежно від вибору т. X, сума квадратів відстаней від X до кожної вершини куба дорівнює 4d2.
139.
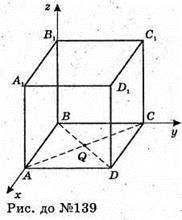
В грань ABCD вписано коло. Нехай а – ребро куба. Розмістимо куб в системі координат. Q – центр кола. 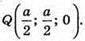
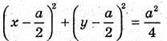 – рівняння кола.
– рівняння кола.
A1(a; 0; a), В1(0; 0; a), С 1(0; a; a), D 1(a; а; а).
З рівняння кола: 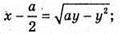
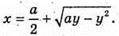
Отже, 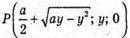 – довільна точка кола.
– довільна точка кола.
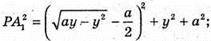
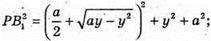
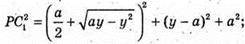
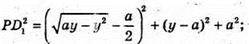
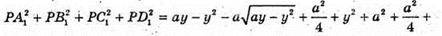
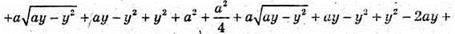
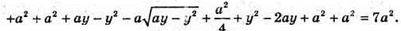
Тобто, сума квадратів відстаней від довільної точки кола до вершин протилежної грані куба – стала величина (7а2), вона не залежить від вибору точки. Залежить лише від довжини ребра.
140.
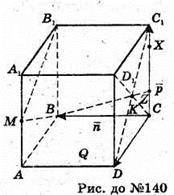
Нехай площина (В1МК) перетинає С1С в т. X. З того, що В1, Μ, K, X лежать в одній площині, (В1МK) можна записати рівність: 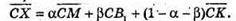
Нехай 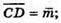
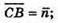
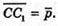
Тоді 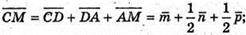
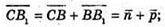
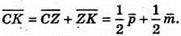
Звідси:
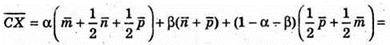
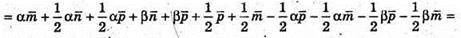
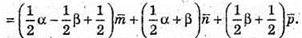
Крім того, 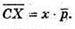
Звідси: 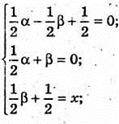
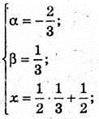
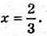
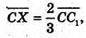 звідси С1Х : ХС =1 : 2.
звідси С1Х : ХС =1 : 2.
141.
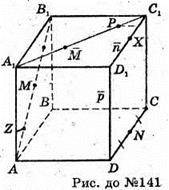
Нехай площина (MNP) перетинає D1C1 в т. X. З того, що Μ, N, Р, X лежать в одній площині (MNP), можна записати рівність 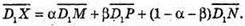
Нехай 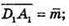
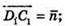
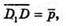 тоді
тоді 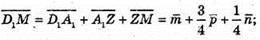
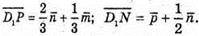
Звідси
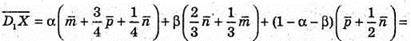
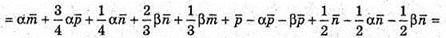
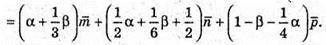
Крім того,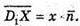
Звідси 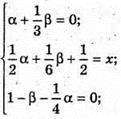
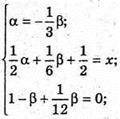
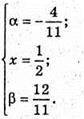
Тобто 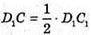 або D1Х : ХС1 = 1.
або D1Х : ХС1 = 1.
Площина (MNP) ділить відрізок D1C1 на дві рівні частини.