Циліндр
940.
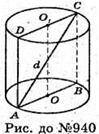
Нехай дано циліндр, ABCD – осьовий переріз циліндра,
AO = r – радіус циліндра, AC = d – діагональ осьового перерізу:
А) ΔABC — прямокутний.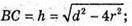 
BC – висота циліндра;
Б) SABCD – площа діагонального перерізу.
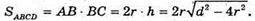
В) Площа бічної поверхні: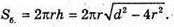 
Г) Площа поверхні циліндра
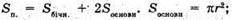
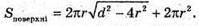
941.
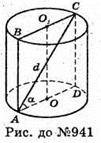
Нехай дано циліндр, діагональ осьового перерізу циліндра дорівнює
D
A) BC = OO1- висота циліндра. ΔABC – прямокутний, BC = d × sin α;
Б) AB – діаметр основи. З ΔАBС: AB = d × cos а;
В) площа основи: Socн. = π × r2, де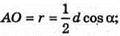 
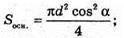
Г) SABCD – площа осьового перерізу циліндра.
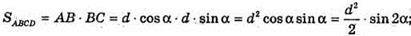
Д) площа бічної поверхні циліндра. Sбічн. = 2π × rh.
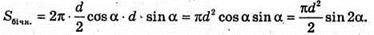
942.
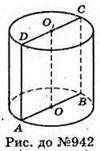
Нехай дано циліндр, площа осьового перерізу – SABCD = S.
Площа бічної поверхні циліндра S бічн. = 2πrh.
Однозначно знайти площу бічної поверхні циліндра
Відповідь: π × S.
943.
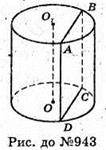
Нехай дано циліндр, ABCD – площина, яка проходить через твірну циліндра, але не дотикається до нього.
ABCD – прямокутник, AD? BC, AB? DC, AD + площині основи циліндра,
AD + DC, отже, площина ABCD перетинає циліндр по прямокутнику.
944.
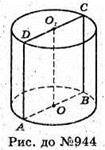
Нехай дано циліндр, площа поверхні якого дорівнює 50 см2, а площа бічної поверхні циліндра дорівнює 30 см2. AO = r; BC = h. Sповн. = 2πrh + 2πr2 = 50;
Sб. = 2πrh = 30; 2πr2 = 50 – 30 = 20; πr2 = 10;
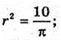
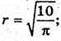
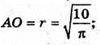
2π × rh = – 30;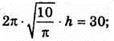 
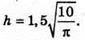
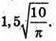
Відповідь: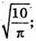 
945.
Нехай з квадрата ABCD, площа якого Q, згорнули бічну поверхню циліндра. Сторона квадрата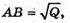 
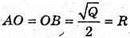– радіус основи циліндра.
Знайдемо площу основи циліндра.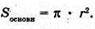 
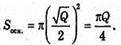
Відповідь: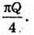 
946.
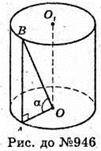
Нехай дано циліндр, OA = r, радіус основи циліндра, твірну AB видно з центра основи O від кутом α. AAOB = α. Sбічн. = 2πrh. Sб. = 2π × AO × АВ.
Розглянемо ΔAOB – прямокутний. AB + AO, ∠BAO = 90°; AB = h = r tg α,
Sбічн.= 2πr2 tg α.
Відповідь: 2πr2 tg α.
947.
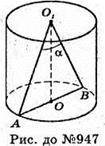
Нехай дано циліндра, діаметр його основи AB = d. Цей діаметр видно з центра другої основи під кутом α, тобто ∠AO1B = α.
Sп. = Sб. + 2Sосн. = 2πrh + 2 πr2 = 2 πr (h + r), де h = O1O, r = AO.
ΔAO1O – прямокутний, O1 O + AB;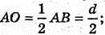 
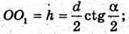
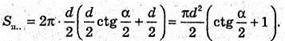
Відповідь: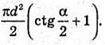 
948.
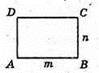
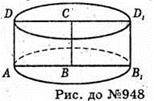
Нехай дано прямокутник ABCD з нерівними сторонами, тобто AB ≠ CD.
Нехай AB = m, CD = n. Якщо прямокутник обертається навколо сторони, що дорівнює n, маємо: AD = h = n; AB = r = m. Sб. = 2π × rh = 2πmn.
Якщо прямокутник обертається навколо сторони, що дорівнює m, маємо:
AD = h = m, AB = r = m; Sб. = 2π × rh = 2πmn. Отже, площі бічних поверхонь циліндрів, утворених обертанням цього прямокутника навколо нерівних сторін, рівні.
949.
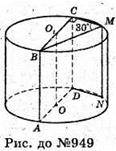
Нехай дано циліндр, де ABCD – переріз, що проходить через вісь циліндра, а площина CMND проходить через твірні циліндра, кут між цими площинами 30°. ∠MCB = 30°.
Нехай CD = h; BC = d. ΔBCM – прямокутний, ∠CMB = 90° (кут, що спирається на діаметр).
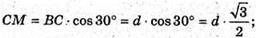SABCD = AB × BC = h × d;
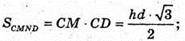
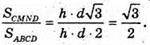
Отже, площі перерізів циліндра площинами, які проходять через його твірну, якщо кут між цими площинами 30°, а одна з площин проходить через вісь циліндра, відносяться як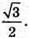 
950.
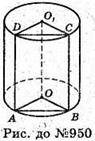
Нехай дано циліндр, радіус основи якого OA = r, а висота O1O = h.
ABCD – площина, яка перпендикулярна до основи циліндра і відтинає від кола дугу 
AB = 60°, це означає, що відповідний центральний кут ∠AOB = 60°.
ΔAOB – рівнобедрений, AO = OB = r,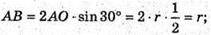 
Sперерізу ABCD = AB × ВС = r × h.
Відповідь: r × h.
951.
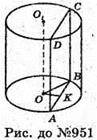
Нехай дано циліндр з висотою OO1 = 16 см, радіусом OB = 10 см. Паралельно вісі циліндра проведена площина ABCD на відстані OK = 60 мм = 6 см.
SABCD = AB × ВС, де BC = OO1= 16 см.
AB знайдемо з ΔOBK.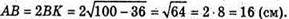 
Отже, SABCD = AB × BC = 16 × 16 = 256 (см2).
Відповідь: 256 см2.
952.
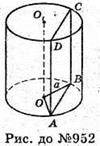
Нехай дано циліндр, паралельно вісі циліндра, радіус основи якого OB = а, проведено площину ABCD, що перетинає основу по хорді АВ, яка стягує дугу, градусна міра якої 90°. Це означає, що центральний кут ∠AOB = 90°. Утворений переріз ABCD – квадрат.
З ΔАОВ: ∠AOB = 90°; AB2 = OB2 + OA2 = 2а2;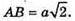 
ABCD – квадрат, отже,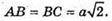 
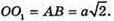
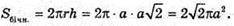
Відповідь: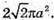 
953.
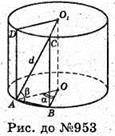
Нехай дано циліндр. Паралельно вісі циліндра проведено площину ABCD, що перетинає нижню основу по хорді AR, яку видно із центра під кутом α.
∠AOB = α.
Діагональ d = AC1, утвореного перерізу утворює з площиною основи кут β, ∠CAB = β. Sбічн. = 2π × r × h, де r = OB, h = OO1.
ΔABC – прямокутний, ∠ABC = 90°. BC = d × sin β; AB = d cos β.
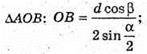
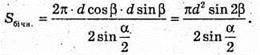
Відповідь: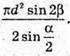 
954.
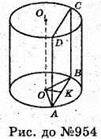
Нехай дано циліндр, радіус основи якого OA = 5 см. На відстані OK від осі циліндра проведено переріз ABCD площею 48 см2, сторони перерізу пропорційні числам 1 і 2, тобто AB : BC = 1 : 2, Знайдемо сторони перерізу.
Нехай AB = х, BC = 2х. AB × BC = 48; x × 2х = 48; 2х2 = 48; x2 = 24;
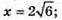
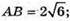
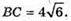
ΔAOK – прямокутний;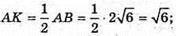 
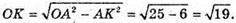
Якщо AB : BC = 2 : 1, то AB = 2х; BC = х;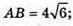 
Тоді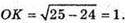 
Відповідь: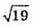 
См або 1 см.
955.
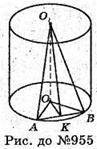
Нехай дано циліндр, твірна якого дорівнює 6 см. Хорду AB нижньої основи видно із центра O основи під кутом ∠AOB = 90°. Відрізок O1K з’єднує центр верхньої основи O з серединою нижньої основи K і утворює з площиною основи кут 60°. ∠O1KO = 60°. Sбічн. = 2πrh, деr = OB, h = OO1,
ΔO1OK – прямокутний; O1O = 6 см;
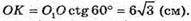
ΔAOK – прямокутний, ∠AOK = 45°;
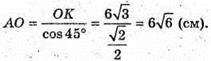
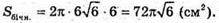
Відповідь: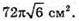 
956.
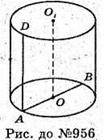
Нехай дано циліндр, твірна якого AD = 5 см, діаметр AB = 20 см.
Sбічн. = 2πrh, де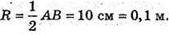 
Sбічн. = 2π × 0,1 × 5 = π = 3,14 (м2).
Додамо на шви 10 % від поверхні, отже жерсті взяти необхідно:
3,14 + 3,14 × 0,1 = 3,14 + 0,314 = 3,454 = 3,5 (м3).
Відповідь: 3,5 м2.
957.
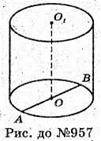
Нехай дано циліндр, діаметр основи якого AB = 1420 мм = 1,42 м.
OO1 = 1 км = 1000 м;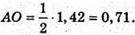 
Sб. ц. = 2πrh = 2π × 0,71 = 1000 = 1420π = 1420 × 3,14 = 4458,8 (м2).
Якщо покрити ізоляційною стрічкою двічі, то S = 4458,8 × 2 = = 8917,8 (м2).
Відповідь: не вистачить.
958.
Нехай дано циліндр, радіус основи якого дорівнює 6 см, AO = 6 см, висота
OO1 = 4 см. Sб. = 2πrh = 2π × 6 × 4 = 48π (см2) = 48 × 3,14 = 150,72 (см2) необхідно матеріалу для виготовлення однієї банки.
15 000 × 0,1 = 1500 м2 – жерсті іде на відходи та шви.
15 000 м2 = 1500 м2 = 13 500 м2 = 135 000 000 см2 – необхідно жерсті для виготовлення банок.
Знайдемо, скільки таких банок можна виготовити з даної жерсті.
135 000 000 см2 : 150,72 см2 = 895 700 (банок).
959.
Нехай дано циліндр, висота якого 3,8 м; діаметр AB = 0,8 м.
Sб. = 2πrR × h = 2π × 0,4 × 3,8 = 2 × 3,14 × 0,4 × 3,8 = 9,5456 м2 = 95 456 см2.
Тиск пари: на 1 см2 пара давить з силою 10 кг.
Тиск пари на повну поверхню котла 9 554 560 кг.
960.
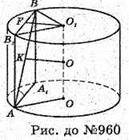
Нехай дано циліндр, точки A i B лежать на різних колах основ циліндра,
∠BAA1 = 60°. OA = R; AB = 2R.
Розглянемо ΔABA1, АА1 = 2R × cos 60° = R.
ΔO1B1F, де O1F + BB1.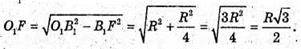 
Відповідь: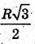 
– відстань від осі циліндра до прямої AB.
961.
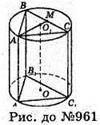
Нехай дано циліндр. Площини перерізів циліндра AA1B1B і AA1C1C проходять через твірну AA1і їх площі дорівнюють 10 м2, а площа перерізу BB1C1C дорівнює 16 см2.
Нехай AA1 = h, тоді AB × AA1 = 10 см2; AC × AA1 = 10 см2; BC × AA1 = 16 см2.
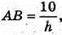Отже,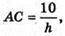 
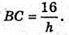
Знайдемо радіус основи циліндра AO1 = O1B = O1C.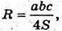 
Де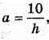 
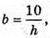
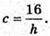
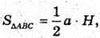
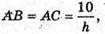
H – висота трикутника ABC; H = AM.
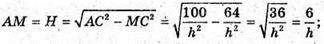
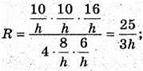
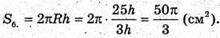
Відповідь: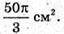 
962.
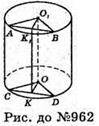
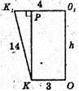
Нехай дано циліндр, площина перетинає основи циліндра по хордах AB = 6 см і CD = 8 см, відстань між якими дорівнює 14 см.
Радіус основи циліндра О1А = O1B = 5 см; AB = 6 см;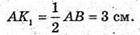 
ΔO1K1B: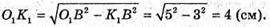 
ΔOKD: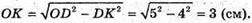 
Проведемо KP + О1K1. ΔK1PK – прямокутний.
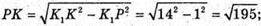
PK = OO1 = h.
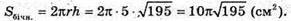
Відповідь: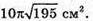 
963.
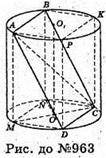
Нехай дано циліндр, вершини прямокутника ABCD лежать на колах основ циліндра, висота OO1 =1,2 см. O1D = 8 см;
O1D ; O1C – радіус основи конуса.
AB : AD = 1 : 2.
M i N – проекції точок А і В. P і K – проекції точок В і C1.
ΔAMC-прямокутний.
AC2 = AM2 + MC2 = 144 + 256 = 400. AC = 20 см.
MC = 2MO1 = 2R = 16 см. AC – діагональ прямокутника.
Нехай AB = х, тоді AD = 2х.
ΔADC – прямокутний.
AC2 = AD2 + DC2;
400 = x2+ 4х2; 5х2 = 400; х2 = 80;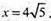 
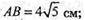
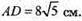
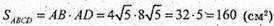
Відповідь: 160 см2.
964.
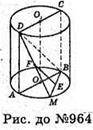
Нехай дано ABCD – осьовий переріз циліндра,
SABCD =240 см2 (площа перерізу).
Точка M лежить на колі нижньої основи, точка E – середина відрізка MB,
Точка F – середина відрізка MD.
EF = 13 см;
ΔΜΒD, EF – середня лінія.
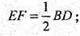BD = 2EF = 26 см.
Нехай AB = х; AD = у, тоді
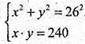
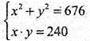
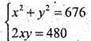
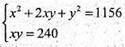
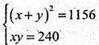
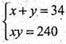
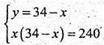
X2- 34х + 240 = 0.
D = 1156 – 960 = 196;
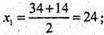
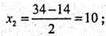
Y1 = 10; y2 = 24
AB = 24 см або AB = 10 см; AO = R = 12 см або 5 см; AD = 10 см або AD = 24 см; AD = H = 10 см або 24 см.
Sцил. = 2πR2+2πRH = 2πR(R + H).
Sцил. = 2π × 12 (12 + 10) = 24π × 22 = 528π см2.
S цил. = 2π × 5 (5 + 24) = 10π × 29 = 290π см2.
Відповідь: 528π см2 або 290π см2.
965.
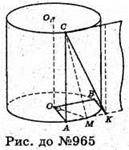
Дано циліндр. Нехай точка M ділить дугу нижньої основи у відношенні 1 : 2.
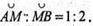∠BOA = 90°.AC – твірна. AC = 8 см.
Радіус основи циліндра OA = 2 см.
Градусна міра дуги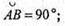 
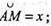
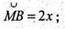
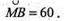
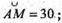
X + 2х = 90°; 3х = 90°; x = 30°;
ΔOBM – рівносторонній OB = OM = BM = R= 2 см.
Відстань від точки В до площини САМ дорівнює BK.
BK + AM. BK=OA = 2 см.
Пряма BC утворює із площиною САМ кут ∠BCK.
CK2 = AC2 + AK2 =64 + 4 = 68;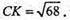 
AB2 = AO2 + OB2 = 4 + 4 = 8;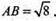 
BC2 = AC2 + AB2 = 64 + 8 = 72;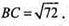 
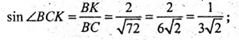
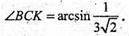
Відповідь: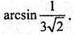 
966.
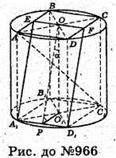
Нехай всі вершини квадрата A1D1FE зі стороною а лежать на бічній поверхні циліндра.
A1E = EF = FD1 = A1D1 = a.
Вісь циліндра OO1 перпендикулярна до однієї сторони квадрата.
EF + OO1. Із площиною квадрата вісь OO1утворює кут α
∠FOO1 = α.
PO1 = PO × sin α.
ΔPOO1-прямокутний. PO1= a × sinα.
ΔA1PO1 – прямокутний. A1O1 – радіус основи циліндра.
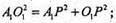
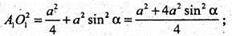
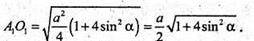
Відповідь: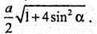 
967.
Нехай дано циліндр. ABCB і MNPK – два взаємно перпендикулярні осьові перерізи циліндра, причому AD і MK належать одній основі.
Точка F – середина твірної АВ.
Площа осьового перерізу ABCD дорівнює площі MKNP = 16 см2.
SперерізуABCD = BC × AB.
Нехай AB = h; тоді BC = 2r; 2r × h = 16 см2.
S бічн.= 2πrh = 16π см2; PN + BC; ∠POC = 90°;
OP2 + OC2 = PC2: PC2 = r2 + r2;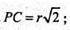 
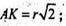
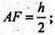FK + AC; r = 2.
Sосн. = πr; Sосн.= 471 см 2;
Sповн. цил. = 2πr2 + 2πrRH = 2πrR(R + H) = 2 × 4π + 16π = 24π (см 2).
968.
Нехай дано правильний тетраедр AB = AD = DC = BC = BH = AC = а.
Правильний тетраедр і циліндр розміщені так, що мимобіжні ребра тетраедра є діаметрами основ циліндра.
AO1 = O1D = OB = OC = R – радіус основи циліндра.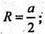 
AB = BC = L – твірна циліндра. L = а.
Sбічн. циліндра= 2πRL
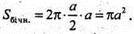
Відповідь: πa2.
969.
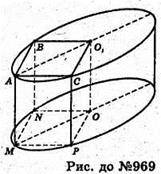
Нехай дві вершини куба O1і O лежать на осі циліндра, а шість вершин куба
А, В, С, М, N, P – лежать на колах основ циліндра, ребро куба ABO1CMNOP дорівнює а.
AB = BO1 = O1C = AC = MN = NO = OP = MP = a.
Висота циліндра OO1 = а.
Радіус циліндра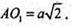 
Відповідь: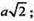 
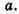
970.
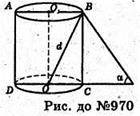
Нехай до циліндра радіуса r проведено дотичну пряму під кутом α до площини його основи. Відстань від центра нижньої основи до цієї прямої – ОМ.
Відстань від центра основи до точки дотику дорівнює d,
OB = d; ZBMC = а; OC = r.
BC2=OB2 – OC2 = d2 – r2.
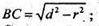
ΔBCM – прямокутний. CM = BC × ctg α;
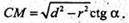
OM = OC + CM;
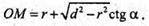
Відповідь: 
(1 votes, average: 5.00 out of 5)
Loading...