Головна ⇒ 📌Довідник с фізики ⇒ Додавання векторів за правилом паралелограма – Елементи векторної алгебри
Додавання векторів за правилом паралелограма – Елементи векторної алгебри
3. Елементи векторної алгебри
3.2. Додавання векторів за правилом паралелограма
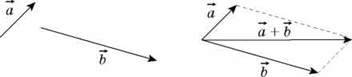
Щоб додати два вектори за правилом паралелограма, треба розмістити їх так, не змінюючи їх напряму, щоб вони виходили з однієї точки, й добудувати на кінцях векторів паралельні прямі. Діагональ одержаного паралелограма, проведена з точки, в якій суміщені початки обох векторів, є їх сумою.
Related posts:
- Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...
- Віднімання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри 3.3. Віднімання векторів Різницею двох векторів, спрямованих по одній прямій або паралельних один одному, є алгебраїчна різниця цих векторів. Щоб знайти різницю двох векторів, які мають різні напрями, треба розмістити обидва вектори так, щоб вони виходили з однієї точки. Потім сполучити кінці векторів вектором, спрямованим від від’ємника до зменшуваного. Цей вектор […]...
- Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Множення вектора на скаляр – Елементи векторної алгебри 3. Елементи векторної алгебри 3.4. Множення вектора на скаляр Приклад: а – 4...
- Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...
- Проекція вектора на координатну вісь – Елементи векторної алгебри 3. Елементи векторної алгебри 3.5. Проекція вектора на координатну вісь Довжину відрізка A1B1 між проекцією початку вектора а і кінця вектора на вісь, взяту зі знаком ” + ” або “-“, називають проекцією вектора на координатну вісь. Проекція додатна, коли напрям руху від проекції початку вектора до проекції кінця збігається із напрямом координатної осі, і […]...
- ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 1. ОСНОВИ КІНЕМАТИКИ 1.2. ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Вектор – напрямлений відрізок. Векторні величини мають числове значення (модуль), напрям, точку прикладання (рис. 3). Рис. З Проекція вектора на вісь Ох – довжина відрізка, який сполучає проекцію початку вектора на вісь Ох з проекцією кінця вектора на ту саму […]...
- Означення паралелограма. Властивості паралелограма Урок № 4 Тема. Означення паралелограма. Властивості паралелограма Мета: домогтися засвоєння учнями означення паралелограма, означення додаткових елементів паралелограма, формулювання і доведення теореми про властивість кутів і сторін паралелограма; сформувати первинні вміння відтворювати вивчені означення і властивості, а також використовувати їх разом із вивченими раніше властивостями та ознаками паралельних прямих для розв’язування задач на доведення та […]...
- Площа паралелограма Геометрія Площі фігур Площа паралелограма Площа паралелограма обчислюється за формулою S = ha, де h – висота, a – сторона, до якої проведена ця висота. Оскільки (див. рисунок), то . Із двох різних висот паралелограма більша та, яка опущена на меншу сторону. AC = d1; BD = d2; ; . Трикутники AOB, BOC, COD, DOA […]...
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...
- Теореми про ознаки паралелограма Урок № 6 Тема. Теореми про ознаки паралелограма Мета: сформувати в учнів свідоме розуміння змісту та схеми доведення теореми, що виражає ознаки паралелограма. Формувати вміння: – відтворювати ознаки та їхні доведення; – застосовувати вивчені ознаки для доведення того, що даний чотирикутник є паралелограмом. Тип уроку: засвоєння нових знань. Наочність та обладнання: конспект “Паралелограм”. Хід уроку […]...
- Властивості паралелограма Урок № 5 Тема. Властивості паралелограма Мета: доповнити знання учнів властивостями бісектрис кутів паралелограма та висот паралелограма; продовжити роботу із формування вмінь відтворювати вивчені означення і властивості паралелограма та використовувати ці твердження під час розв’язування задач на обчислення і доведення. Тип уроку: застосування знань, умінь та навичок. Наочність та обладнання: конспект “Паралелограм”. Хід уроку I. […]...
- Площа прямокутника. Площа паралелограма Урок № 45 Тема. Площа прямокутника. Площа паралелограма Мета: закріпити знання учнів про: – зміст та властивості площі многокутника; – зміст теореми про площу прямокутника та його наслідок. Сформулювати та довести теорему про площу паралелограма. Продовжувати формувати вміння відтворювати зміст вивчених понять та теорем, а також використовувати їх під час розв’язування задач на обчислення площ […]...
- Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...
- Ознака паралельності прямих Геометрія Стереометрія Ознака паралельності прямих Теорема. Дві прямі, паралельні третій прямій, паралельні між собою. Із цієї теореми випливає, що середини сторін просторового чотирикутника (див. рисунок) є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині). Зверніть увагу: якщо ABCD – просторовий чотирикутник, то його діагоналі AC і BD – мимобіжні прямі....
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Алгебра векторів 1. Побудуємо вектори – одиничний вектор 2. Побудуємо вектори 3. Побудуємо вектори 4. Побудуємо вектори 5. 6. 1) Побудуємо вектори 2) Побудуємо вектори 7. Побудуємо вектори 8. 1) 2) 9. Побудуємо вектори Вектори та рівні. 10. Накреслимо два ненульові вектори Побудуємо Побудуємо Таким чином, 11. Побудуємо вектори Вектори протилежно напрямлені. 12. Побудуємо вектори 13. 1) […]...
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Елементи-метали в Періодичній системі – Метали Хімія Неорганічна хімія Метали Елементи-метали в Періодичній системі Якщо в Періодичній системі провести діагональ від Берилію до Астату, то зліва внизу розміщуватимуться елементи-метали (до них же належать елементи побічних підгруп). Атоми металів порівняно легко віддають електрони, перетворюючись на позитивно заряджені йони. Це пояснюється тим, що в атомів металів: – мале число електронів на зовнішньому енергетичному […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Паралелограм Геометрія Чотирикутники Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника. Вершини чотирикутника називаються Сусідніми, якщо […]...
- БІОГЕННІ ЕЛЕМЕНТИ Екологія – охорона природи БІОГЕННІ ЕЛЕМЕНТИ – хім. елементи, що постійно входять до складу всіх організмів. В основному це 22 елементи, співвідношення яких у живій і неживій матерії різне....
- Скалярний добуток векторів. Кут між векторами 233. А) Якщо то α = 90°, α – кут між векторами. Б) то α – гострий; А) то α – тупий. 234. А) Б) В) Г) 235. А) Б) 236. А) Б) В) Г) 237. А) Б) В) 238. α – кут між векторами А) Б) В) Г) 239. А) Звідси Б) Звідси В) […]...
- Векторний добуток векторів 1. Векторний добуток векторів є вектором, а скалярний – числом. Векторний та скалярний добуток мають однакові властивості (крім комутативності). 2. За означенням модуля векторного добутку А отже, оскільки то 3. 1) За означенням У нашому випадку Скористаємось основною тригонометричною тотожністю: Тоді 2) За означенням У нашому випадку Скористаємось основою тригонометричною тотожністю: Тоді Оскільки 3) Рівність […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Застосування векторів 269. 5(х – 2) + 0 × (у + 1) – 3(z – 4) = 0; 5x – 10 – Зz + 12 = 0; 5x – Зz + 2 = 0 – рівняння шуканої площини. 270. 3(x – 1) – 4(y – 2) + 7(z + 3) = 0; 3x – 3 – 4у […]...
ТИЧИНКИ »