Двогранні кути
520.
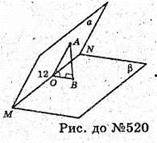
Нехай дано двогранний кут, міра якого 60°, ∠AOB = 60°. AO + MN, BO + MN, АВ + β, АВ = 12 см. ΔАОВ – прямокутний.
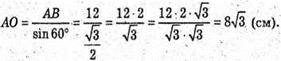
521.
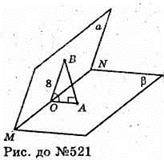
Нехай дано двогранний кут, який дорівнює 45°. т. В? α, ОВ = 8 дм.
АВ + β. Δ ΟΒΑ – прямокутний.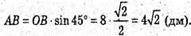 
522.
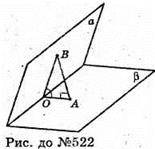
Нехай дано двогранний кут ∠BOA.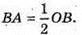 
Катет ВА лежить проти ∠О і вдвічі менше гіпотенузи ОВ, отже ∠BOA = 30°, а міра двогранного кута 30°.
523.
Нехай з точок А і В однієї грані гострого двогранного кута
Опущено перпендикуляри АA1, BBt на другу грань і АА2, ВВ2 – на ребро.
АА1 = 3 дм, АА2 = 5 дм, ВВ1 = 9 дм. АА1 + a, ВВ2 + a, отже, A1A? B2B.
АА1 + a; Β1Β2 + а, отже, А1А2 ? В1В2. ∠A2 = ∠Β2, ∠Α1 = ∠B1, ΔАА2А1 – ΔBB2B1.
З подібності трикутників маємо: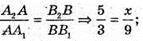 
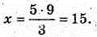
Відповідь: 15 см.
524.
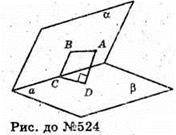
Нехай точка А віддалена від грані α на АВ = 3 дм; від грані β на АВ = 4 дм.
АС – відстань від точки А до ребра а двогранного кута.
ABCD – прямокутник. ΔADC – прямокутний.
АС2
Відповідь: 5 дм.
525.
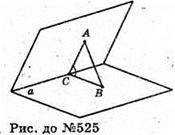
Нехай двогранний кут дорівнює 60°. ∠ACB = 60°. СА + а; СА = 3,2 дм;
СВ + a; СВ = 1,2 дм.
Розглянемо ΔABC.
За теоремою косинусів маємо: АВ2 = АС2 + ВС2 – 2AС × ВС cos 60°;
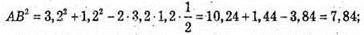
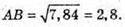
Відповідь: 2,8 дм.
526.
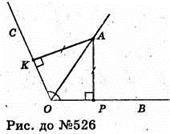
Нехай з точки А на грані двогранного кута опущені перпендикуляри
АК + ОС; АР + О В; АК = АР = 36 см; ∠COB = 120°; ΔΑΚΟ = ААРО
(прямокутні: АО – спільна, АK =АР). ∠ΑΟΚ = ∠ΑΟΡ = 60°;
ΔАОK – прямокутний.
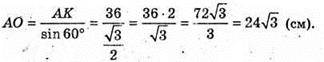
Відповідь: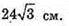 
527.
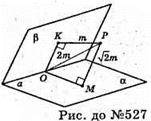
Нехай дано двогранний кут, точка Р лежить всередині кута, віддалена від його граней на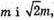 
а від ребра на 2m. PM + α, 
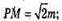РК + β; РK = m. РО = 2m.
ΔΟΡΜ – прямокутний, ∠ΡΟΜ = 90°;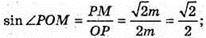 
∠ΡΟΜ = 45°; ΔОКР – прямокутний, ∠ΡΟΚ = 90°;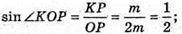 
∠ΡΟΜ = 30°. Міра двогранного кута: ∠KOM = ∠ΚΟΡ + ∠ΡΟΜ = 30° + 45° = 75°. Відповідь: 75°.
528.
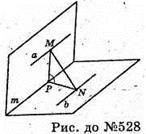
Нехай дано двогранний кут з ребром, прямі а і b лежать у гранях двогранного кута, а? b. MN – відстань між цими паралельними прямими, MN = 13 см;
МР + m; МР = 7 см; NP + m; NP = 8 см. (прямі а і b віддалені від ребра кута на відстані МР і PN). ∠MPN – лінійний кут двогранного кута.
Розглянемо ΔΜΡΝ. Знайдемо кут Р.
ΜΝ2 = МР2 + ΡΝ2 – 2МР × PN × cos ∠P;
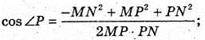
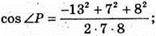
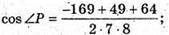
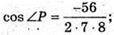
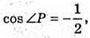
Отже ∠P = 120°.
Отже, міра двогранного кута ∠MPN = 120° .
Відповідь: 120°.
529.
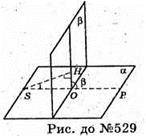
Нехай міра двогранного кута 100°. ∠HOP = 100°, тоді ∠HOS = 80°. ΔHOS – прямокутний. SH + β, ∠HSO — кут між площиною однієї його грані і перпендикуляром до другої грані. ∠HSO = 10°.
Відповідь: 10°.
530.
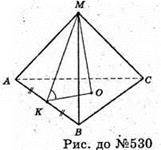
Нехай МАВС – зображення правильного тетраедра. МО + пл. ΔABC.
OK + AB, АK = KB; МK + АВ за теоремою про три перпендикуляри.
Отже, ∠MKO – лінійний кут одного з двогранних кутів правильного тетраедра.
531.
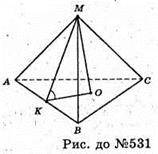
Нехай МАВС – зображення правильного тетраедра. ∠MKO – лінійний кут двогранного кута при ребрі АВ. Нехай ребро тетраедра АВ = a. OK = г – радіус кола, вписаного в тетраедр.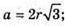 
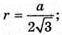
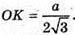
ΔАМК – прямокутний, AM = а;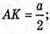 
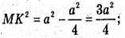
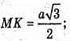
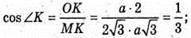
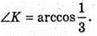
Відповідь: міра двогранного кута правильного тетраедра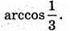 
532.
А)
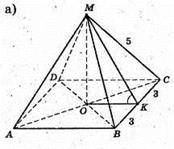
Нехай дано правильну чотирикутну піраміду MABCD, бічне ребро МС = 5 см, ребро основи АВ = 6 см. МО + (ABCD), OK + ВС, МK + ВС за теоремою про три перпендикуляри. ∠MKO – лінійний кут двогранного кута при ребрі основи. ОК – радіус кола, вписаного в основу правильної чотирикутної піраміди, ОK = 3 см.
ΔМKС – прямокутний, МK + КС, ∠MKC = 90°, МК = 4 см. ΔAMOK — прямокутний, ∠MKO – лінійний кут при ребрі основи піраміди.
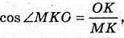
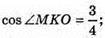
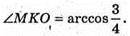
Б)
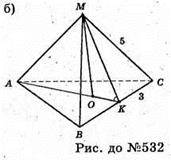
Нехай дано правильну трикутну піраміду МАВС, бічне ребро якої дорівнює 5 см, МС = MB = МА = 5 см, ВС = 6 см, ВС – ребро основи.
МО + пл. ΔАВС, OK + ВС, МК + ВС (за теоремою про три перпендикуляри). ∠MKO – лінійний кут двогранного кута при ребрі основи.
ΔМKС – прямокутний, МK = 4 см, ОK – радіус кола, вписаного в основу піраміди.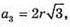 
де r = ОK,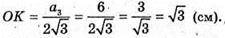 
ΔMOK – прямокутний.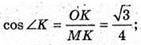 
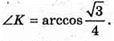
Відповідь: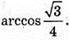 
533.
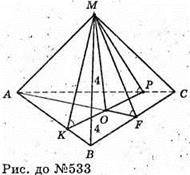
Нехай дано піраміду, в основі якої лежить трикутник зі сторонами АВ = 13 см, ВС = 14 см, АС =15 см, а всі двогранні кути при основі рівні. Висота піраміди МО = 4 см. Якщо всі двогранні кути при основі піраміди рівні, то вершина піраміди проектується в центр кола, вписаного в основу піраміди.
МО + (ΔABC). OK = OF = OP = r – радіус вписаного кола. OK + АВ, МK + АВ, ∠MKO – лінійний кут двогранного кута при ребрі основи піраміди. ОК = г,
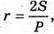де S – площа ΔАВС, Р – периметр ΔАВС.
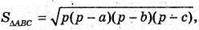де 
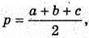
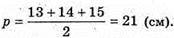
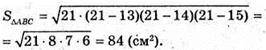
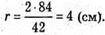∠MKO = 45°.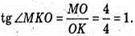 
Відповідь: 45°.
534.
Нехай дано піраміду SABCD, у якої ребро перпендикулярне до площини
Основи ABCD і дорівнює BD.
A)
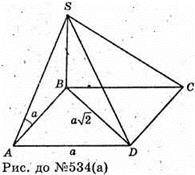
ABCD – квадрат, SB + пл. кв. ABCD.
1) Міра двогранного кута при ребрі AD.
∠SAB – лінійний кут двогранного кута при ребрі AD.
SB + пл. ABCD; АВ + AD; AS + AD.
Нехай АВ = а,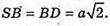 
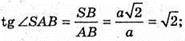
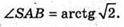
2) Міра двогранного кута при ребрі DC.
SB + (ABCD), ВС + CD, SC + CD, ∠SCB – лінійний кут при ребрі CD.
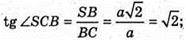
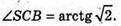
3) Міра двогранного кута при ребрі SB.
АВ + SB; СВ + SB; ∠ABC – лінійний кут двогранного кута при ребрі SB.
∠ABC = 90°.
Б)
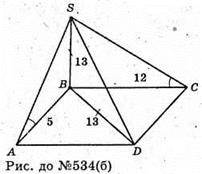
Нехай основа піраміди SABCD – прямокутник зі сторонами 5 см і 12 см.
АВ = 5 см; ВС = 12 см; SB = BD; ΔABD: BD2 = АВ2 + AD2; ВD2 = 25 + 144 = 169; BD = 13; SB = BD = 13(см).
1) Міра двогранного кута при ребрі АВ ∠SAB – міра двогранного кута при ребрі АВ.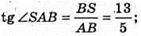 
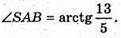
2) Міра двогранного кута при ребрі DC. ∠SCB – міра двогранного кут при ребрі DC.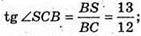 
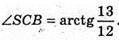
3) Міра двогранного кута при ребрі BS. АВ + BS, ВС + BS, ∠ABC = 90°.
В) Нехай основа піраміди ромб, у якого ∠BAD = 60°. BS + (ABCD).
1) SF + DC, BF + DC. ∠SFB – лінійний кут двогранного кута при ребрі DC.
BP + AD, SP + AD, ∠SPB – лінійний кут двогранного кута при ребрі AD.
∠SFB = ∠SPB.
ΔABD – різносторонній. АВ = BD = AD = а.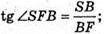 
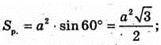S = DC × BF;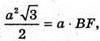 
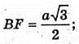
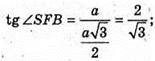
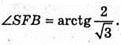
Г)
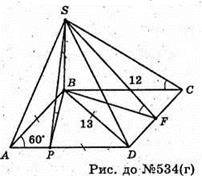
Нехай основа піраміди – паралелограм зі сторонами 4 см і 6 см та кутом
∠ABC = 120°.
ΔABD; BD2 = АВ2 + AD2 – 2АВ × AD cos 60°;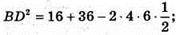 
BD2 = 16 + 36 – 24; BD2 = 28;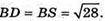 
SB + (ABCD). BK + DC, SK + DC; ∠SKB – лінійний кут двогранного кута при ребрі DC.
SB + (ABCD); BF + AD; SF + AD. ∠SFB – лінійний кут двогранного кута при ребрі AD.
ΔABF – прямокутний.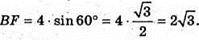 
ΔВСК – прямокутний.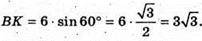 
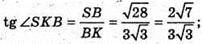
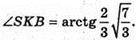
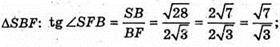
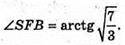
536.
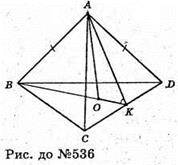
Нехай дано тетраедр ABCD, у якого АВ + АС, АВ + AD, АС + AD. AB = АС = АD.
ΔАВС = ΔAACD = ΔABD (за двома рівними катетами). Отже, ВС = CD = BD, тому ΔDBC – рівносторонній. Проведемо АО перпендикулярно площині ΔBCD. OK + CD, тоді AK + CD (за теоремою про три перпендикуляри).
∠АКО – міра двогранного кута при ребрі CD.
Нехай ВС = CD = BD = а, ОК – радіус кола, вписаного в рівносторонній ΔBCD.
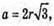
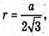де r = ОК.
ΔACD – рівнобедрений прямокутний трикутник. АK – висота і медіана.
СК = KD, ∠ACK = ∠CAK = 45°.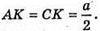 
ΔАСК.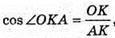 
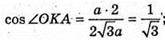
Кути при ребрах ВС, BD, CD рівні.
Відповідь: 
537.
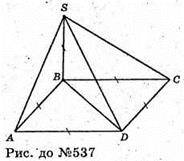
Нехай дано піраміду SABCD, в основі якої лежить квадрат ABCD.
SB + (ABCD). SB = AB = ВС = CD = AD. AB + AD, SB + (ABCD),
Тоді за теоремою про три перпендикуляри SA + AD,
∠SAB – міра двогранного кута при ребрі AD.
Аналогічно ∠SCB – міра двогранного кута при ребрі CD.
∠SBC – міра двогранного кута при ребрі AB. ∠SBC = 90°, AB + BS.
ΔABS – міра двогранного кута при ребрі ВС. ∠ABS = 90°, BC + SC.
∠SAB = ∠SCB = 45°.
∠SAB = ∠SCB – рівнобедрені прямокутні трикутники.
Відповідь: 90° , 90°, 45°, 45°.
538.
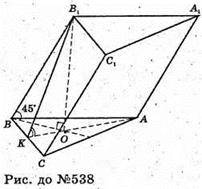
Нехай дано зображення похилої трикутної призми ABCA1B1C1,
Основою якої є правильний ААВС зі стороною а. АВ = ВС = АС = а.
О – центр основи ΔАВС. О – проекція точки В1. ВO1 + площині ΔАВС.
OK + ВС, тоді за теоремою про три перпендикуляри B1K + ВС.
∠B1KO – міра двогранного кута при ребрі ВС. ∠B1BO = 45°.
О – центр ΔАВС. ОB – радіус кола, описаного навколо ΔАВС.
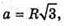
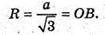
ΔBB1O – прямокутний, В1O = ВО,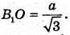 
ΔB1OK – прямокутний.
ОK – радіус кола, вписаного в рівносторонній трикутник
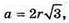
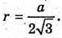
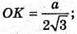
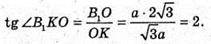∠B1KO = arctg 2.
539.
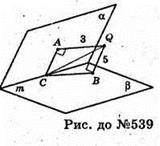
Нехай точка Q лежить всередині двогранного кута, міра якого 60°,
Точка Q віддалена від граней на 3 см і 5 см. AQ + α, AQ = 3 см;
QB + β, QB = 5 см.
QC – відстань від точки Q до ребра цього кута (m – ребро кута).
ΔАСО – прямокутний. ∠BCQ = x, тоді ∠ACQ = 60° – х.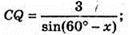 
ΔQCB – прямокутний.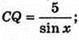 
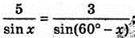
5 sin(60° – x) = 3 sin х; 5 sin 60° cos х – 5 cos 60° sin х = = 3 sin х;
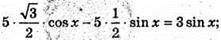
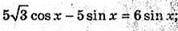
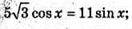
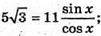
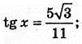
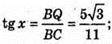
BQ = 5;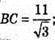 
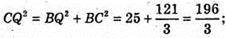
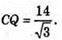
540.
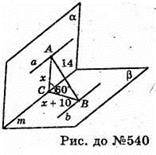
Нехай величина двогранного кута 60° = ∠ACB. а? b,
Відстань між ними 14 см. АС + m, ВС + m. Нехай ВС – АС = 10 см.
Нехай АС = х, тоді ВС = х + 10.
ΔΑВС: за теоремою косинусів маємо;
АВ2 = АС2 + ВС2 – 2АС × ВС × cos 60°;
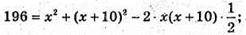
196 = х2 + x2 + 20x + 100 – x2 – 10x; x2 + 10x – 96 = 0; D = 100 + 4 × 96 = 484;
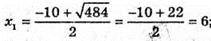
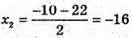(не задовольняє умові задачі).
Отже, АС = 6 см, BС = 16 см.
Відповідь: 6 см, 16 см.
541.
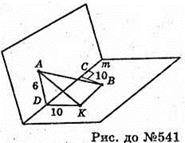
Нехай кінці відрізка АВ належать різним граням двогранного кута і віддалені від його ребра m на AD = 6 см, ВС = 10 см, AD + m, ВС + m, міра кута 120°. Відстань між основами перпендикулярів АВ і ВС дорівнює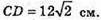 
Проведемо DK + m, DK = 10.
ΔАВК. ∠ADK – 120°, за теоремою косинусів знайдемо АK.
АК2 = АВ2 + DK – 2AD × DK × cos∠ADK;
АК2 = 36 + 100 – 2 × 6 × 10 × cos 120° = 136 + 60 = 196;
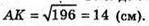
ΔАВК – прямокутний, m X пл. ΔADK, m + DC, ВK + DC. ∠AKB = 90°,
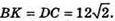
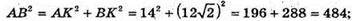
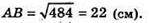
Відповідь: 22 см.
542.
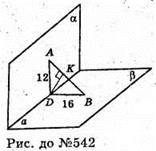
Нехай дано прямий двогранний кут з ребром а.
Кінці відрізка АВ лежать на гранях двогранного кута і віддалені від його ребра на 12 см і 16 см. AD + a. AD = 12 см, BD + a, BD = 16 см.
В площині ΔADВ проведемо DK + АВ. Оскільки а + (AABD), DK ∠(AABD),
То
А + DK, отже, DK – відстань від відрізка АВ до ребра двогранного кута.
З ΔABD за теоремою Піфагора: АВ2 = AD2 + BD2; АВ2 = 122 + 162 = 400;
АВ = 20 см. AD2 = AB x AK;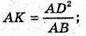 
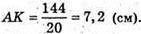
ΔADK – прямокутний, за теоремою Піфагора маємо: DK2 = AD2- АК2;
DK2 = 144 – 51,84 = 92,16;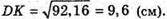 
Відповідь: 9,6 см.
543.
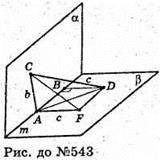
Нехай дано точки А і В на ребрі двогранного кута міри φ.
AC + m, BD + m, m – ребро кута. АС = b, BD = а, АВ = а.
Проведемо AF + АС, AF = с. ∠CAF = φ.
ΔACF, за теоремою косинусів знайдемо CF.
CF2= АС2 + AF2- 2АС × AF × cos φ;
CF2 = b2 + с2 – 2bc cos φ.
ΔCFD – прямокутний, m + c, m? FD.
∠ CFD = 90°. CD2 = CF2 + FD2.
CD2 = b2 + c2 + a2 – 2bc cos φ;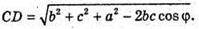 
Відповідь: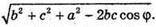 
544.
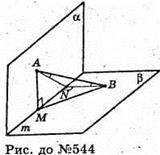
Нехай кінці відрізка АВ лежать у гранях двогранного кута, AM – відстань від точки А до ребра m, АМ + m, BN – відстань від точки В до ребра m. BN + m.
AM = BN за умовою.
З рівності трикутників кути ∠ABM = ∠BAN. ΔАМВ = ΔNAB, АВ – спільна,
AM = NB. Отже, ∠ABM = ∠BAN, що й треба довести.
545.
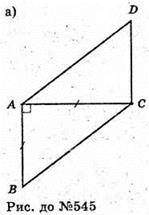
Нехай дано паралелограм ABCD, у якого АВ = АС, АВ +АС. Його зігнули по діагоналі АС так, що ∠BAD = 60°. Тоді сторона AD належить площині α, a сторона АВ лежить у площині β. АС – ребро двогранного кута.
Проведемо AF + m, де m – ребро двогранного кута. ∠FAB – міра двогранного кута при ребрі m, або міра двогранного кута, утвореного площинами трикутників ΔABC і AADC. ΔАВС – прямокутний.
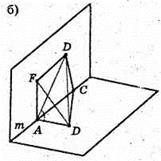
Нехай АВ = АС = а, тоді ВС2 = а2 + а2 = 2а2;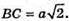 
FA + m, АВ + m, тоді ∠FAB = α – міра двогранного кута, утвореного площинами трикутників ABC і ADC.
Розглянемо ΔABD. ∠A = 60°. BD2 = AD2 + АВ2 – 2AD × АВ ×cos60°;
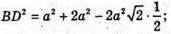
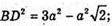
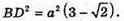
ΔFDB – прямокутний.
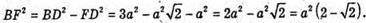
ΔFAB. За теоремою косинусів маємо: FB2 = FA2 + АВ2 – 2FA × AB × cos∠FAB;
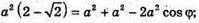
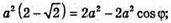
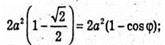
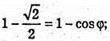
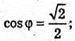φ = 45°.
Відповідь: 45°.
546.
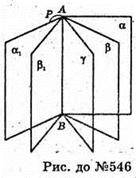
Геометричним місцем точок двогранного кута, рівновіддалених від його граней, є півплощина, яка виходить з ребра даного двогранного кута і ділить кожний його лінійний кут навпіл.
Якщо через АВ даного двогранного кута провести півплощини α1 і β1, перпендикулярні відповідно до граней а і β двогранного кута, дістанемо новий двогранний кут Р. Кожна точка даного кута Р і його внутрішньої області також рівновіддалена від граней а і β даного двогранного кута. Шуканим геометричним місцем точок є об’єднання бісектора даного двогранного кута і двогранного кута F (разом з його внутрішньою областю).
548.
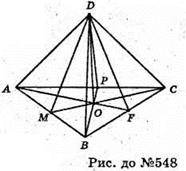
Нехай ABCD – тетраедр. Бісектори всіх двогранних кутів будь-якого тетраедра проходять через точку D – вершину тетраедра.
(1 votes, average: 5.00 out of 5)
Loading...