Формула Герона
УРОК № 13
Тема. Формула Герона
Мета уроку: виведення формули Герона для площі трикутника. Формування вмінь учнів застосовувати виведену формулу до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Площі трикутників і чотирикутників” [13].
Вимоги до рівня підготовки учнів: використовують формулу Герона під час розв’язування задач.
Хід уроку
І. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при
Задача 1. Розв’язання
Оскільки квадрат і ромб мають однакові периметри, то їхні сторони рівні. Нехай довжина сторони дорівнює а, тоді площа квадрата дорівнює а2, а площа ромба a2sin?, де? – кут ромба.
Оскільки sin? < 1, то a2sin? < а2. Отже, площа ромба менша за площу квадрата.
Відповідь. Квадрат.
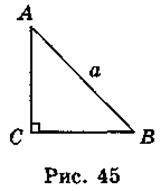
Задача 2. Розв’язання
Оскільки в трикутнику ABC (рис. 45) АВ = а,  CAB = 45°, то АС = АВ • cos
CAB = 45°, то АС = АВ • cos  CAB = a • cos45° = a •
CAB = a • cos45° = a • 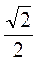 =
= 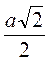 .
.
S? AВC =  AC2 =
AC2 =
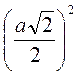 =
= 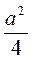
Відповідь. 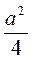 .
.
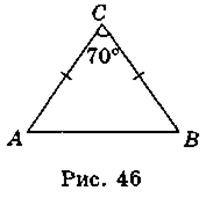
Задача 3. Розв’язання
Нехай у трикутнику ABC (рис. 46) АС = ВС = 1 м,  С = 70°, тоді S =
С = 70°, тоді S =  • AC • BC • sinC =
• AC • BC • sinC =  • 1 • 1 • sin70° =
• 1 • 1 • sin70° =  • sin70°
• sin70° 
 • 0,94 = 0,47 (м2).
• 0,94 = 0,47 (м2).
Відповідь.  0,47 м2.
0,47 м2.
Математичний диктант
1) Знайдіть площу прямокутника зі сторонами 2 см і 3 см. 2) Знайдіть площу прямокутного трикутника з катетами 3 см і 2 см. 3) Знайдіть площу правильного трикутника зі стороною 2 см. 4) Знайдіть площу паралелограма зі сторонами 2 см і  см, якщо кут між сторонами становить 60°. 5) Знайдіть площу ромба, діагоналі якого дорівнюють 3 см і 4 см. 6) Знайдіть площу трикутника, сторони якого дорівнюють
см, якщо кут між сторонами становить 60°. 5) Знайдіть площу ромба, діагоналі якого дорівнюють 3 см і 4 см. 6) Знайдіть площу трикутника, сторони якого дорівнюють  см і 3 см, а кут між ними становить 135°.
см і 3 см, а кут між ними становить 135°.
Відповіді. 1) 6 см2; 2) 3 см2; 3)  См2; 4) 3 см2; 5) 6 см2; 6) 1,5 см2.
См2; 4) 3 см2; 5) 6 см2; 6) 1,5 см2.
II. Сприймання й усвідомлення нового матеріалу
Ви навчилися знаходити площу довільного трикутника за відомими:
1) стороною і висотою, проведеною до цієї сторони; 2) сторонами і кутом між ними.
Сьогодні ми ознайомимося з тим, як можна знайти площу трикутника, якщо відомі три його сторони. Цю формулу одержав Герон Олександрійський, давньогрецький учений, який жив в Александрії в І ст. н. є. Відомо, що він був ученим-інженером, займався геодезією і прикладною математикою.
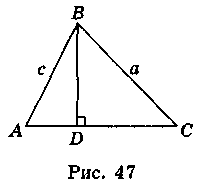
Проведемо висоту до найбільшої сторони трикутника ABC (рис. 47). Нехай АС = b – найбільша сторона цього трикутника, АВ = с, ВС = а, BD AC. Нехай AD = х, тоді DC = b – х. Із прямокутного трикутника ABD маємо: BD2 = c2 – x2. Із прямокутного трикутника BCD маємо: BD2 = а2 – (b – x)2. Тоді маємо рівняння с2 – х2 = a2 – (b – х)2, з якого знайдемо х.
AC. Нехай AD = х, тоді DC = b – х. Із прямокутного трикутника ABD маємо: BD2 = c2 – x2. Із прямокутного трикутника BCD маємо: BD2 = а2 – (b – x)2. Тоді маємо рівняння с2 – х2 = a2 – (b – х)2, з якого знайдемо х.
С2 – х2 = а2 – b2 + 2bx – x2; 2bx = c2 + b2 – a2; 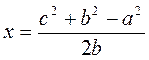 .
.
Тоді BD = 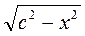 =
= 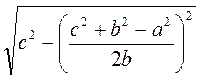 =
= 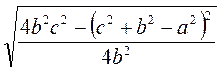 .
.
Отже, S =  B • ВD =
B • ВD = 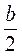
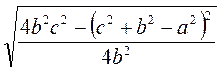 =
= 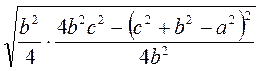 =
= 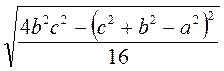 =
= 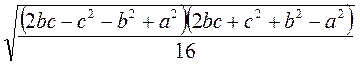 =
=
= 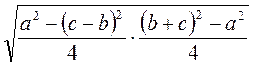 =
= 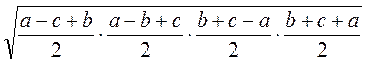 =
= 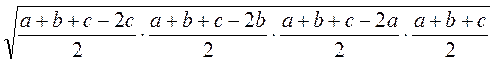 .
.
Ураховуючи, що 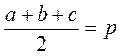 , маємо:
, маємо:
S = 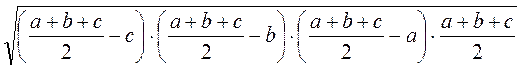 =
=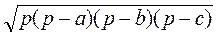 .
.
Що і треба було довести.
Колективне розв’язування задач
Знайдіть площу трикутника за трьома сторонами:
А) 17, 65, 80; б) 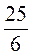 ,
, 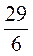 , 6; в) 15, 37
, 6; в) 15, 37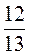 , 47
, 47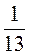 ; г) 2
; г) 2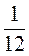 , 3
, 3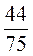 , 1,83.
, 1,83.
Розв’язання
А) S = 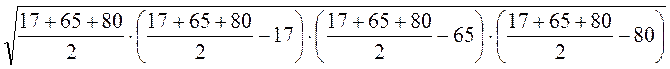 =
= 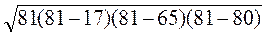 =
= 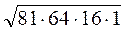 = 288.
= 288.
Б) 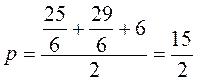 .
.
S = 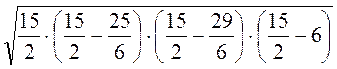 =
= 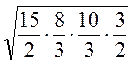 = 10.
= 10.
В) 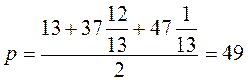 .
.
S = 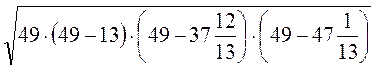 =
= 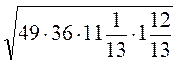 = 42
= 42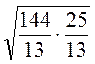 =
= 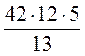 =
= 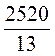 = 193
= 193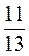 .
.
Г) 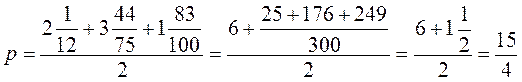 .
.
S=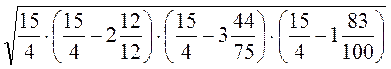 =
=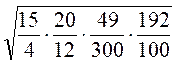 =
=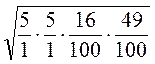 =
= 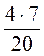 =
= 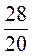 = 1,4.
= 1,4.
ІІІ. Закріплення й осмислення нового матеріалу
Колективне розв’язування задач
Сторони трикутника дорівнюють а, b, с. Знайдіть висоту трикутника, опущену на сторону с.
Розв’язання
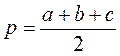 ,
, 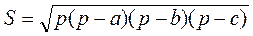 .
.
Оскільки S =  Chc, то hc =
Chc, то hc = 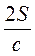 =
= 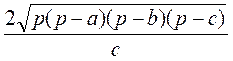 .
.
Відповідь. 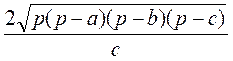 .
.
Самостійне розв’язування задач
Бічні сторони трикутника дорівнюють 30 см і 25 см. Знайдіть висоту трикутника, опущену на основу, що дорівнює: а) 25 см; б) 11 см.
Розв’язання
А) 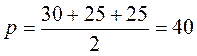 ,
,
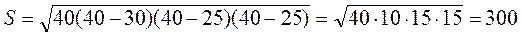 (см2).
(см2).
S =  • 25 • h, 300 =
• 25 • h, 300 =  • 25 h, h =
• 25 h, h = 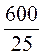 = 24 (см).
= 24 (см).
Відповідь. 24 см.
Б) 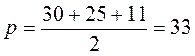 ,
,
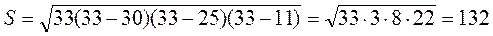 (см2).
(см2).
S =  • 11 • h, 132 =
• 11 • h, 132 =  • 11 • h, h =
• 11 • h, h = 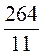 = 24 (см).
= 24 (см).
Відповідь. 24 см.
Колективне розв’язування задачі
Периметр рівнобедреного трикутника дорівнює 64 см, а його бічна сторона на 11 см більша від основи. Знайдіть висоту трикутника, опущену на бічну сторону.
Розв’язання
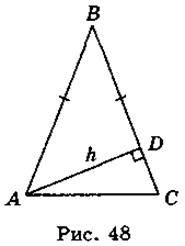
Нехай трикутник ABC (рис. 48) рівнобедрений, АВ = ВС. Нехай АС = х см, тоді АВ = ВС = (х + 11) см. Оскільки периметр дорівнює 64 см, то маємо:
X + 11 + x + 11 + x = 64; 3х + 22 = 64; 3х = 42; х = 14. Отже, АС = 14 см, АВ = ВС = 25 см.
Оскільки 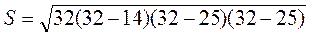 =
=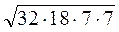 = 7 • 4 • 6 = 168 (см2), S =
= 7 • 4 • 6 = 168 (см2), S =  • АВ • h, то h =
• АВ • h, то h = 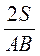 =
= 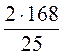 = 13,44 (см).
= 13,44 (см).
Відповідь. 13,44 см.
IV. Самостійна робота
Варіант 1
1. Знайдіть найменшу висоту трикутника зі сторонами 5, 5, 6. 2. Знайдіть найбільшу висоту трикутника зі сторонами 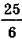 ,
, 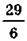 , 6.
, 6.
Варіант 2
1. Знайдіть найменшу висоту трикутника зі сторонами 17, 65, 80. 2. Знайдіть найбільшу висоту трикутника зі сторонами 13, 37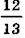 , 47-
, 47-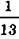 .
.
Розв’язання до завдань самостійної роботи
Варіант 1
1. 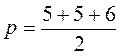 = 8,
= 8, 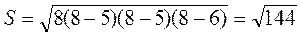 = 12(см2).
= 12(см2).
S =  • 6 h, h = –
• 6 h, h = –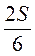 =
= 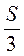 =
= 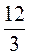 = 4 (см).
= 4 (см).
Відповідь. 4 см.
2. S = 10 см 2. S =  •
• 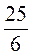 • h, h =
• h, h = 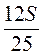 =
= 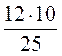 =
= 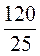 = 4,8 (см).
= 4,8 (см).
Відповідь. 4,8 см.
Варіант 2
1. 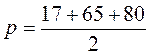 = 81,
= 81, 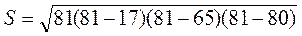 = 288(см2).
= 288(см2).
S =  • 80 • h, h =
• 80 • h, h = 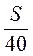 =
= 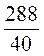 = 7,2 (см).
= 7,2 (см).
Відповідь. 7,2 см.
2. S = 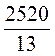 см 2. S =
см 2. S =  • 13 • h, h =
• 13 • h, h = 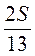 =
= 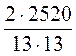 =
= 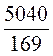 = 29
= 29 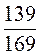 (см).
(см).
Відповідь. 29 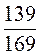 см.
см.
V. Домашнє завдання
Розв’язати задачі.
1. Знайдіть площу трикутника за трьома сторонами, що дорівнюють:
А) 13, 14, 15; б) 5, 5, 6.
2. Знайдіть висоти трикутника, у якого сторони дорівнюють 13 см, 14 см, 15 см. 3. Знайдіть висоту трикутника зі сторонами 2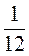 , 3
, 3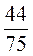 , 1,83, яка проведена на основу 2
, 1,83, яка проведена на основу 2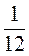 .
.
VI. Підбиття підсумків уроку Завдання класу
1. Запишіть відомі вам формули для знаходження площі трикутника. 2. Знайдіть площу трикутника, якщо його сторони дорівнюють 3 см, 3 см і 2 см.