Куля
Геометрія
Тіла обертання
Куля
Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається Центром кулі, а дана відстань – Радіусом кулі. Межа кулі називається Кулевою поверхнею, або Сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, називається Діаметром. Куля є тілом обертання, яке утворюється під час обертання півкруга навколо його діаметра як осі. Будь-який переріз кулі площиною є круг. Центр цього круга
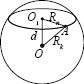
На рисунку у
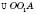
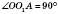, OA – радіус кулі, 
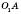– радіус перерізу, 
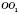– відстань від центра кулі до площини перерізу (d).
.
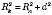Площина, яка проходить через центр кулі, називається Діаметральною площиною. Переріз кулі діаметральною площиною називається Великим кругом, а переріз сфери – Великим колом, або Екватором.
Будь-яка діаметральна площина кулі є її площиною симетрії. Центр
Площина, яка проходить через точку А кульової поверхні та є перпендикулярною до радіуса, проведеного в точку А, називається Дотичною площиною. Точка А називається Точкою дотику.
Дотична площина має з кулею тільки одну спільну точку – точку дотику.
Пряма, яка належить дотичній до кулі площині й проходить через точку дотику, називається Дотичною до кулі в цій точці. Вона має з кулею тільки одну спільну точку. Лінією перетину двох сфер є коло.
Площа сфери радіусом R обчислюється за формулою
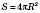.Кульовим сегментом називається частина кулі, яку відтинає від неї січна площина.
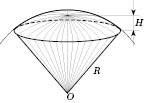
На рисунку H – висота кульового сегмента.
Кульовий сегмент обмежується частиною сфери, площа якої обчислюється за формулою
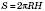, і кругом, який називається Основою сегмента.Кульовий сектор – це кульовий сегмент і конус, вершина якого в центрі кулі, а основою є основа сегмента.
