Кут між площинами
Урок 55
Тема. Кут між площинами
Мета уроку: формування поняття кута між площинами та вмінь учнів знаходити кути між площинами.
Обладнання: стереометричний набір, модель куба.
Хід уроку
1. Фронтальне опитування.
1) Що таке кут між прямою і площиною?
2) Чому дорівнює кут між прямою і площиною, якщо відомо, що пряма:
А) паралельна площині;
Б) перпендикулярна до площини?
3) В яких межах знаходиться кутова міра кута між прямою і площиною?
4) Чи правильно, що:
А) пряма, яка перетинає паралельні площини, перетинає
Б) площина, яка перетинає паралельні прямі, перетинає їх під однаковими кутами?
2. Відповіді на запитання учнів, що виникли в них при виконанні домашніх задач.
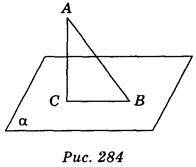
Задача № 36.
Дано: АВ = а; АС ?; 1)
?; 1)  ABC = 45°; 2)
ABC = 45°; 2)  ABC = 60°;
ABC = 60°;  ABC = 30° (рис. 284).
ABC = 30° (рис. 284).
Знайти: ВС.
1) BC = AB cos  ABC = a cos 45° =
ABC = a cos 45° = 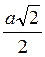 ;
;
2) ВС = AB cos  ABC = a cos60° =
ABC = a cos60° = 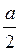 ;
;
3) BC = AB cos  ABC = a cos 30° =
ABC = a cos 30° = 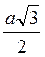 .
.
B і д
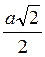 ; б)
; б) 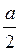 ; в)
; в) 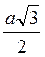 .
.Задача № 38.
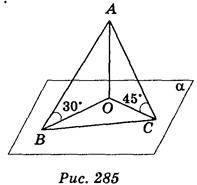
Дано: АО ?; АО = a;
?; АО = a;  ABO = 30°;
ABO = 30°;  ACO = 45°;
ACO = 45°;
 CAB = 90° (рис. 285).
CAB = 90° (рис. 285).
Знайти: ВС.
1) Із? АОВ АВ = 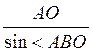 =
= 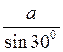 = 2a.
= 2a.
2) Із? АОС АС = 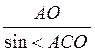 =
= 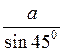 = a
= a .
.
3) Із? АВС ВС = 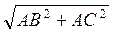 =
= 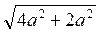 = а
= а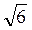 .
.
Відповідь. а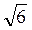 .
.
Задача № 40.
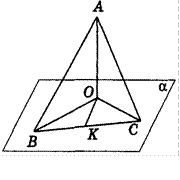
Дано: АО ? ; АО = а;
? ; АО = а;  ABO =
ABO =  ACO = 30°;
ACO = 30°;  BOC = 120° (рис. 286).
BOC = 120° (рис. 286).
Знайти: ВС.
1) ?АОВ = ?АСО, звідси BO = CO.
2) Із? АОС OC = AO ctg  ACO = a ctg
ACO = a ctg  30° = a
30° = a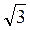 .
.
3) ?ВОС – рівнобедрений. Проведемо OK ВС, тоді
ВС, тоді  BOK =
BOK =  KOC = 120° : 2 = 60°.
KOC = 120° : 2 = 60°.
4) Із? ОKС КС = ОС sin  KOC = а
KOC = а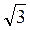 Sin60° =
Sin60° =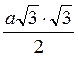 =
=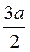 .
.
Тоді ВС = 2КС = 2 – 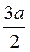 = 3а.
= 3а.
Відповідь. 3а.
3. Математичний диктант.
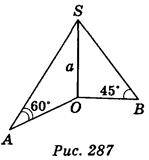
SO (ABO), SA і SB – похилі, SO = а, <AOB = 90°.
(ABO), SA і SB – похилі, SO = а, <AOB = 90°.
Варіант 1.  SAO = 60°,
SAO = 60°,  SBO = 45° (рис. 287).
SBO = 45° (рис. 287).
Варіант 2.  SAO = 45°,
SAO = 45°,  SBO = 30° (рис. 288).
SBO = 30° (рис. 288).
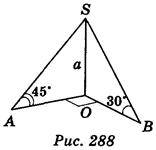
Користуючись зображенням, знайдіть:
1) проекцію похилої SA на площину АОВ; (2 бали)
2) довжину похилої SA; (2 бали)
3) проекцію похилої SB на площину АОВ; (2 бали)
4) довжину похилої SB; (2 бали)
5) відстань між основами похилих; (2 бали)
6) відстань між прямими SO і АВ. (2 бали)
Відповідь. Варіант 1. 1) 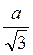 ; 2)
; 2) 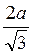 ; 3) а; 4) a
; 3) а; 4) a ; 5)
; 5) 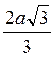 ; 6)
; 6) 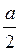 .
.
Варіант 2. 1) а; 2) а ; 3) а
; 3) а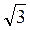 ; 4) 2а; 5) 2а; 6)
; 4) 2а; 5) 2а; 6) 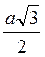 .
.
Нехай дано дві площини? і?, які перетинаються по прямій с (рис. 289). Проведемо площину, яка перпендикулярна до прямої с, вона перетне площини? і? по прямих а і b. Кут між прямими а і b називається кутом між площинами? і?.
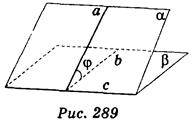
Кут між двома площинами, які перетинаються,- це кут між прямими перетину цих площин із площиною, перпендикулярною до лінії перетину даних площин. Якщо площини паралельні, то кут між ними дорівнює 0°. Якщо площини перпендикулярні, то кут між ними дорівнює 90°. Отже, якщо? – кут між площинами, то 0°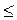 ?
?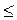 90°. Далі учні самостійно знайомляться з доведенням того, що означений так кут між площинами не залежить від вибору січної площини, за підручником (§ 4, п. 33).
90°. Далі учні самостійно знайомляться з доведенням того, що означений так кут між площинами не залежить від вибору січної площини, за підручником (§ 4, п. 33).
Розв’язування задач
1. Дано зображення куба. Знайдіть кут між площинами АВС і ABD (рис. 290).
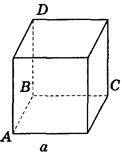
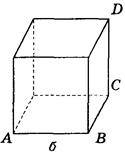
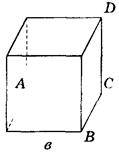
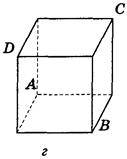
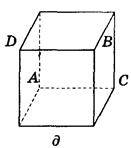
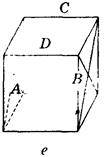
Рис. 290
Відповідь, а) 90°; б) 45°; в) arctg 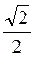 ; г) 2arctg
; г) 2arctg 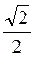 ; д) 0°; е) 90°.
; д) 0°; е) 90°.
2. Задача № 43 із підручника (с. 57).
3. Задача № 44 із підручника (с. 57).
4. Задача № 46 із підручника (с. 58).
5. Задача № 47 із підручника (с. 58).
§4, п. 33; контрольне запитання № 16; задачі № 42, 45 (с. 57).
1) Дайте означення кута між площинами.
2) Чи залежить величина кута між площинами від вибору січної площини?
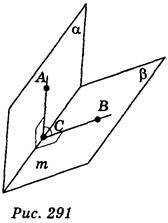
3) Площини? і? перетинаються по прямій m (рис. 291), точка А належить площині?, точка В – площині?, точка С – прямій m; АС M, ВС
M, ВС M, <ACB = 60°. Укажіть, які з наведених тверджень правильні, а які – неправильні:
M, <ACB = 60°. Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) площина АВС перпендикулярна до прямої m;
Б) кутом між площинами? і? є кут між прямими ВС і m;
В) кут між площинами? і? дорівнює куту між прямою АС і площиною?;
Г) кут між площинами? і? більший 60° ;
Д) кут між площинами? і? дорівнює 120°.