Кут між векторами. Скалярний добуток векторів
Урок 59
Тема. Кут між векторами. Скалярний добуток векторів
Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач.
Обладнання: схема “Вектори в просторі”
Хід уроку
1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233).
2. Відповіді на запитання, які виникли в учнів при розв’язуванні задач № 51-53.
3. Математичний диктант.
Дано вектори:
Варіант
 (3; 0; 4);
(3; 0; 4);  (7; 0; 2);
(7; 0; 2);Варіант 2 –  (2; -2; 0);
(2; -2; 0);  (3; 0; -3).
(3; 0; -3).
Запишіть:
1) координати вектора 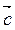 , якщо
, якщо 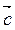 =
=  +
+  , (2 бали)
, (2 бали)
2) координати вектора 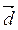 , якщо
, якщо 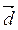 = 2
= 2 –
–  ; (2 бали)
; (2 бали)
3) довжину вектора  +
+  ; (2 бали)
; (2 бали)
4) координати вектора 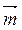 , якщо відомо, що довжина вектора
, якщо відомо, що довжина вектора 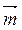
 ; (2 бали)
; (2 бали)5) при якому значенні k вектор 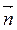 (k; 0; 6) колінеарний вектору
(k; 0; 6) колінеарний вектору  ; (2 бали)
; (2 бали)
6) чи компланарні вектори  ,
,  та
та 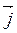 (0; 0; 1)? (2 бали)
(0; 0; 1)? (2 бали)
Відповідь. Варіант 1. 1) 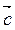 (10; 0; 6). 2)
(10; 0; 6). 2) 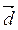 (-1; 0; 6). 3) 2
(-1; 0; 6). 3) 2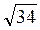 . 4)
. 4) 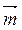 (-9; 0; -12),
(-9; 0; -12), 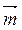 (9; 0; 12). 5) k = 21. 6) Так.
(9; 0; 12). 5) k = 21. 6) Так.
Варіант 2. 1) 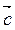 (5; -2; -3). 2)
(5; -2; -3). 2) 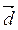 (1; -4; 3). 3)
(1; -4; 3). 3) 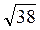 . 4)
. 4) 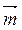 (6; -6; 0),
(6; -6; 0), 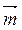 (-6; 6; 0). 5) k = – 6. 6) Hi.
(-6; 6; 0). 5) k = – 6. 6) Hi.
Скалярним добутком векторів  (аx; аy; аz) •
(аx; аy; аz) •  (bx; by; bz) називається число (скаляр)
(bx; by; bz) називається число (скаляр)  –
–  = аx – bx + аy – by + аz – bz.
= аx – bx + аy – by + аz – bz.
1. Знайдіть  –
–  , якщо
, якщо  (-2; 3; 1),
(-2; 3; 1),  (-4; -5; 2).
(-4; -5; 2).
2. Дано вектори  (2; -1; 4),
(2; -1; 4),  (5; 3; n). При якому значенні п скалярний добуток векторів дорівнює -3?
(5; 3; n). При якому значенні п скалярний добуток векторів дорівнює -3?
Із означення скалярного добутку двох векторів  і
і  випливають його властивості.
випливають його властивості.
1)  –
–  =
=  –
–  .
.
2) ( +
+  ) –
) – 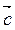 =
=  –
– 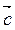 +
+  –
– 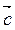 .
.
3) Скалярний добуток векторів  і
і  дорівнює добутку їх абсолютних величин на косинус кута між ними:
дорівнює добутку їх абсолютних величин на косинус кута між ними:  –
–  =
=  –
–  cos? (рис. 297).
cos? (рис. 297).
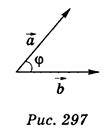
Від точки О відкладемо вектор OВ =  (рис. 298) і ОА =
(рис. 298) і ОА =  . Виберемо декартову систему координат так, щоб точка О була початком координат, пряма ОА збіглася з віссю у, вісь z була б перпендикулярна до прямої ОА і знаходилася в площині ОАВ, вісь х перпендикулярна до площини уz. Визначимо координати векторів
. Виберемо декартову систему координат так, щоб точка О була початком координат, пряма ОА збіглася з віссю у, вісь z була б перпендикулярна до прямої ОА і знаходилася в площині ОАВ, вісь х перпендикулярна до площини уz. Визначимо координати векторів  і
і  :
:
А(0; | | ; 0); B(0; |
| ; 0); B(0; | | cos?; |
| cos?; | | sin?);
| sin?);  (0; |
(0; | |; 0);
|; 0);  (0; |
(0; | | cos?; |
| cos?; | | sin?).
| sin?).
Знайдемо скалярний добуток:
 –
–  = 0 – 0 + |
= 0 – 0 + | | – |
| – | | cos? + 0 – |
| cos? + 0 – | | sin? = |
| sin? = | | – |
| – | | cos?.
| cos?.
Наслідки із властивості 3:
1) 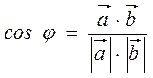
2) Два відмінні від нуля вектори  і
і  перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
Дійсно, якщо  –
–  = 0, то
= 0, то  –
–  – cos? = 0 , cos? = 0, ? =
– cos? = 0 , cos? = 0, ? = 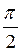 , і навпаки, якщо? = 0 , то
, і навпаки, якщо? = 0 , то  –
–  =
=  –
–  – cos? =
– cos? =  –
–  – 0 = 0.
– 0 = 0.
1. Знайдіть  –
–  , якщо
, якщо  = 5,
= 5,  = 4, а кут між векторами дорівнює 120°.
= 4, а кут між векторами дорівнює 120°.
2. Ребро куба дорівнює 4 (рис. 299). Знайдіть 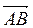 –
– 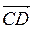 .
.
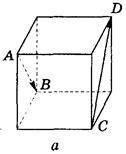
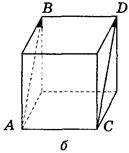
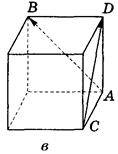
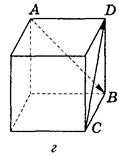
Рис. 299
3. Чи перпендикулярні вектори  (2; 3; 6) і
(2; 3; 6) і  (3; 2; -1)?
(3; 2; -1)?
4. При якому значенні т вектори  (6; 0; 12) і
(6; 0; 12) і  (-8; 13; m) перпендикулярні?
(-8; 13; m) перпендикулярні?
5. Чи є серед векторів  (2; 3; 1),
(2; 3; 1),  (5; 9; 2),
(5; 9; 2), 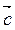 (-3, 1; 3) ортогональні вектори?
(-3, 1; 3) ортогональні вектори?
6. Який кут утворюють вектори  (-5; 0; 0) і
(-5; 0; 0) і  (0; 3; 0)?
(0; 3; 0)?
7. Знайдіть кут між векторами  (1; 1; 0) і
(1; 1; 0) і  (1; 0; 1).
(1; 0; 1).
8. Знайдіть cos ABC, якщо А(1; -3; 4), В(2; -2; 6), С(3; 1; 3).
III. Домашнє завдання
§4, п. 35, 36; контрольні запитання № 18-20; задачі № 55 (1; 4), 56 (с. 58).
IV. Підведення підсумку уроку
1) Що називається скалярним добутком векторів  (аx; аy; аz) і
(аx; аy; аz) і  (bx; by; bz)?
(bx; by; bz)?
2) Сформулюйте властивості скалярного добутку векторів.
3) Яка умова ортогональності двох ненульових векторів?
4) У просторі дано вектори  (1; 1; -1),
(1; 1; -1),  (0; -1; 1). Укажіть, які з вказаних тверджень правильні, а які – неправильні:
(0; -1; 1). Укажіть, які з вказаних тверджень правильні, а які – неправильні:
А) 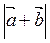 = 1;
= 1;
Б) вектори  і
і  перпендикулярні;
перпендикулярні;
В) вектори  +
+  і
і  не перпендикулярні;
не перпендикулярні;
Г)  -(
-( +
+ ) = 1;
) = 1;
Д) вектори  і
і  +
+  утворюють кут, косинус якого дорівнює
утворюють кут, косинус якого дорівнює 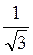 .
.