Головна ⇒ 📌Довідник з математики ⇒ Логарифмічні нерівності
Логарифмічні нерівності
Математика – Алгебра
Логарифмічна функція
Логарифмічні нерівності
Розв’язуючи логарифмічні нерівності, спираються на такі твердження.
1. Якщо 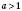 , то нерівність
, то нерівність 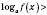
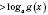 рівносильна подвійній нерівності
рівносильна подвійній нерівності 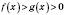 .
.
Це твердження можна записати у вигляді:
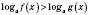
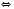
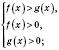
або 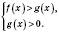
2. Якщо 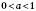 , то нерівність
, то нерівність
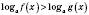 рівносильна подвійній нерівності
рівносильна подвійній нерівності 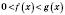 .
.Це твердження можна записати у вигляді:
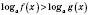
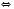
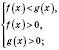
або
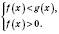
Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо виписувати ОДЗ, оскільки все одно буде необхідно розв’язувати систему нерівностей, яка включає й ОДЗ.
Приклади
1)
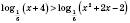 .
.Логарифмічна функція
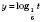 з основою
з основою 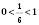 спадна, отже, дана нерівність
спадна, отже, дана нерівність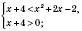
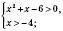
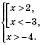

Відповідь:
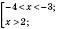 (або у вигляді
(або у вигляді 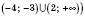 .
.2)
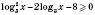 .
.Нехай
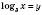 .
.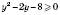 ,
, 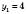 ,
, 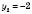 .
.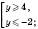
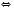
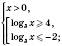
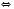
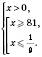

Відповідь:
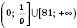 або
або 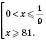
3)
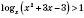 .
.Розглянемо два випадки.
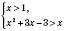
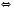
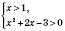
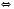
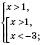
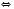
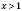 .
.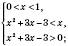
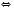
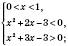
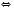
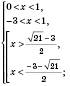
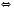
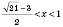 .
.Об’єднуючи ці проміжки, одержимо відповідь.
Відповідь:
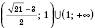 .
.4)
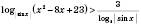 .
.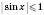 ; основою логарифма може бути тільки додатне число, яке не дорівнює 1. Виходячи з цього, отримуємо, що дана нерівність рівносильна системі:
; основою логарифма може бути тільки додатне число, яке не дорівнює 1. Виходячи з цього, отримуємо, що дана нерівність рівносильна системі: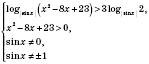
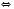
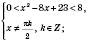
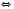
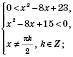
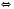
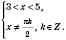
Якщо
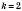 , то
, то 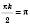 ;
; 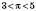 .
.Якщо
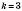 , то
, то 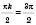 ;
; 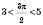 .
.Відповідь:
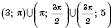 .
.Related posts:
- Нерівності з однією змінною УРОК № 63 Тема. Нерівності з однією змінною Тестові завдання 1. Дано нерівності: 1) -2х2 + х + 6 < 0; 2) 2х2 + х + 7 ? 0; 3) х2 > 0; 4) -3х2 – х – 6 < 0. 2. Яка з даних нерівностей виконується при будь-яких значеннях x? а) усі; б) 2; […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Рівняння. Нерівності зі змінною Рівняння. Нерівності зі змінною 1 Розбий записи на дві групи. Назви кожну групу. 27 + х = 51 27 + х < 51 40 ∙ р > 160 2 Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, […]...
- Логарифмічні функції Математика – Алгебра Логарифмічна функція Логарифмічні функції Функцію називають Логарифмічною функцією з основою a. Логарифмічна та показникова функції є взаємно оберненими. Властивості логарифмічної функції : Графіки показникової (рисунок 1) і логарифмічної (рисунок 2) функцій з однаковою основою симетричні відносно прямої . Рис. 1 Рис. 2...
- Лінійні нерівності та їхні системи УРОК № 61 Тема. Лінійні нерівності та їхні системи Тестове завдання 1. Знайдіть переріз проміжків (-6; 7] і (-4; 25]. А) [7; 25); б) [-4; 7); в) (-6; 25]; г) (-4; 7]. 2. Розв’яжіть нерівність . A) k < 1,125; б) k? ; в) k? 1,125; г) немає розв’язків. 3. При яких х має зміст […]...
- Розв’язування показникових нерівностей УРОК 50 Тема. Розв’язування показникових нерівностей Мета уроку. Формування умінь учнів розв’язувати показникові нерівності. І. Перевірка домашнього завдання 1. Відповіді на запитання, що виникли в учнів при виконанні домашніх завдань. 2. Усне розв’язування показникових нерівностей з використанням таблиці 21 для усних обчислень “Показникові нерівності “. 1 2 3 4 5 1 2х > 8 2х […]...
- Логарифмічні рівняння УРОК 57 Тема. Логарифмічні рівняння Мета уроку. Формування умінь учнів розв’язувати логарифмічні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 15-25 із “Запитання і завдання для повторення” розділу V та відповіді на запитання, які виникли в учнів у процесі виконання домашніх завдань. 2. Виконання вправ, аналогічних домашнім: № 47 (1; 3), 51. II. […]...
- Розв’язування логарифмічних нерівностей УРОК 61 Тема. Розв’язування логарифмічних нерівностей Мета уроку. Формування умінь учнів розв’язувати логарифмічні нерівності І. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні цих завдань. II. Сприймання і усвідомлення розв’язування логарифмічних нерівностей (які розв’язуються введенням нової змінної) Приклад 1. Розв’яжіть нерівність log х – log5 […]...
- Лінійні нерівності з однією змінною УРОК № 12 Тема. Лінійні нерівності з однією змінною Мета уроку: домогтися закріплення учнями змісту: означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми Ті розв’язування залежно від різних значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язування нерівностей з однією змінною, що містять дроби із числовими […]...
- Рівняння. Нерівності зі змінною Мета: узагальнити й систематизувати навчальний досвід учнів відносно рівнянь і нерівностей зі змінною, способів їх розв’язування. Дидактичні задачі. Вдосконалювати навички позатабличного множення та ділення – усна лічба. Класифікувати записи на рівності та нерівності зі змінною. Актуалізувати поняття рівняння, “розв’язок рівняння”, “розв’язати рівняння”; поняття нерівності зі змінною; розуміння способу добору числа для розв’язування рівнянь та нерівностей. […]...
- Ірраціональні нерівності Математика – Алгебра Степенева функція Ірраціональні нерівності Приклади 1) Відповідь: . 2) Відповідь: ....
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 4. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ Ви вже знаєте чотири арифметичні дії над числами – додавання, віднімання, множення і ділення. Щоб записати, яку саме дію над числами треба виконати, використовують числові вирази. Наприклад, записи 24 + 2, 24 – 2, 24 ∙ 2, 24 : 2 […]...
- Розв’язування нерівностей з однією змінною Математика – Алгебра Нерівності Розв’язування нерівностей з однією змінною Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків. Числові проміжки […]...
- Рівняння. Нерівності. Геометричний матеріал Рівняння. Нерівності. Геометричний матеріал 753. Прочитайте твердження. До кожного з них доберіть відповідне рівняння. 1. Невідоме число збільшили у 6 разів і отримали число 4206. 2. Різницю чисел х і 215 збільшили у 6 разів і отримали число 2916. 3. Невідоме число зменшили на добуток чисел 215 і 6 та отримали число 3246. 4. Невідоме […]...
- Розв’язування нерівностей, що містять показникову функцію УРОК 49 Тема. Розв’язування нерівностей, що містять показникову функцію Мета уроку. Познайомити учнів зі способами розв’язування показникових нерівностей. І. Перевірка домашнього завдання Відповіді на запитання, що виникли в учнів під час виконання домашніх завдань. II. Аналіз самостійної роботи, проведеної на попередньому уроці ІІІ. Сприймання і усвідомлення розв’язування найпростіших показникових нерівностей та тих, що безпосередньо зводяться […]...
- НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...
- Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...
- РОЗВ’ЯЗУВАННЯ ТА СКЛАДАННЯ ЗАДАЧ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ. РІВНЯННЯ І НЕРІВНОСТІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ЗАКРІПЛЮВАТИ ВМІННЯ СКЛАДАТИ ЗАДАЧІ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ; ДОСЛІДИТИ МОЖЛИВОСТІ ПЕРЕБУДОВИ ЗАДАЧ НА ЗАДАЧІ НА ПРОПОРЦІЙНИЙ ПОДІЛ I. Перевірка домашнього завдання Фронтально скласти план розв’язування задачі 847. Взаємоперевірка обчислення виразів вправи 848. II. Актуалізація та корекція опорних знань учнів 1. Усні обчислення. Змагання двох команд гравців. 1 команда 2 команда 350 • (430 […]...
- Повторення. Математичні вирази, рівності та нерівності Повторення. Математичні вирази, рівності та нерівності 1 Розбий математичні вирази на дві групи. Прочитай математичні вирази різними способами. 420 + 350 618 – а х + у 920 – 460 7 ∙ с 151 ∙ 4 408 : 3 n : 14 Значення яких виразів ти можеш знайти? Знайди їх значення. Чого не вистачає, щоб […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Розв’язування тригонометричних нерівностей УРОК 30 Тема. Розв’язування тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати тригонометричні нерівності. І. Перевірка домашнього завдання. 1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання. 2. Фронтальна бесіда з учнями з використанням рис. 135. 1) Які дуги відповідають нерівностям: Tg t > a, tg t < a, tg t > […]...
- Контрольна робота № 7 (підсумкова) УРОКИ 63-70 Уроки 63-70 відповідають V розділу програми з алгебри та початків аналізу “Резерв навчального часу”, і вчитель може використовувати цей час на власний розсуд з урахуванням рівня математичної підготовки учнів. Ці години можна використати на повторення на початку навчального року, як додаткові години на окремі теми або для узагальнення й систематизацію матеріалу і повторення […]...
- УТВОРЕННЯ, ЧИТАННЯ ТА ЗАПИСУВАННЯ П’ЯТИЦИФРОВИХ ЧИСЕЛ У МЕЖАХ 20 000. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ. НЕРІВНОСТІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ОЗНАЙОМИТИ З УТВОРЕННЯМ, ЧИТАННЯМ ТА ЗАПИСОМ П’ЯТИЦИФРОВИХ ЧИСЕЛ У МЕЖАХ 20 000; ПОВТОРИТИ ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ; ФОРМУВАТИ ВМІННЯ ЗНАХОДИТИ ЗНАЧЕННЯ НЕВІДОМИХ У НЕРІВНОСТЯХ; УДОСКОНАЛЮВАТИ ВМІННЯ ПОРІВНЮВАТИ ЗАДАЧІ I. Перевірка домашнього завдання Взаємоперевірка учнями виконаних завдань один у одного в парах. II. Актуалізація та корекція опорних знань учнів 1. Завдання […]...
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Розв’язування логарифмічних рівнянь Математика – Алгебра Логарифмічна функція Розв’язування логарифмічних рівнянь Логарифмічними рівняннями називають такі рівняння, які містять змінну під знаком логарифма. Найпростішим логарифмічним рівнянням є , де , . Корінь цього рівняння дорівнює . Рівняння , де , , рівносильне системі: Зверніть увагу: у цій системі можна випустити одну з нерівностей. Із цього випливає, що для розв’язання […]...
- Порівняння натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 2. Порівняння натуральних чисел Одне з двох різних натуральних чисел завжди більше або менше від іншого. Це означає, що натуральні числа можна порівнювати. Число 5392 більше за число 837 тому, що 5392 – чотирицифрове число, а 837 – трицифрове. Числа 5392 і […]...
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Нерівність трикутника Урок № 38 Тема. Нерівність трикутника Мета: домогтися засвоєння змісту теореми, що виражає нерівність трикутника та схему її доведення та наслідку з теореми; виробляти вміння відтворювати формулювання доведених на уроці тверджень та застосувати для розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Нерівність трикутників та наслідки […]...