Логарифмічні рівняння
УРОК 57
Тема. Логарифмічні рівняння
Мета уроку. Формування умінь учнів розв’язувати логарифмічні рівняння.
І. Перевірка домашнього завдання
1. Фронтальна бесіда за № 15-25 із “Запитання і завдання для повторення” розділу V та відповіді на запитання, які виникли в учнів у процесі виконання домашніх завдань.
2. Виконання вправ, аналогічних домашнім: № 47 (1; 3), 51.
II. Засвоєння поняття найпростіших логарифмічних рівнянь та методів їх розв’язування
Логарифмічними рівняннями називають рівняння, які містять змінну
Приклади логарифмічних рівнянь: lg х = 1 + lg2x, log3(x + 3) = 9,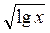 
= 
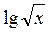і т. д.
Розв’язати логарифмічне рівняння – це означає знайти всі його корені або довести, що рівняння коренів не має.
Найпростіше логарифмічне рівняння має вигляд log х = b, де а > 0, а? 1, х > 0. За означенням логарифма випливає, що х = аb.
Інший вигляд найпростішого логарифмічного рівняння такий: loga x = loga b, де а > 0, а? 1, х > 0, b > 0.
Із цього рівняння випливає, що х = b. Дійсно із рівності loga x = loga b на підставі означення логарифма і основної логарифмічної тотожності маємо: x =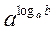 
Найпростішим логарифмічним рівнянням є рівняння logx a = b, де х > 0, х? 1, а > 0.
За означенням логарифма маємо: хb = а, звідси х =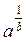 
.
В основному, всі логарифмічні рівняння, які ми будемо розв’язувати, зводяться до розв’язування найпростіших рівнянь.
Приклад 1. Розв’яжіть рівняння log3 (2x + 1) = 2.
За означенням логарифма маємо:
2х + 1 = 32, 2х = 8, х = 4.
Перевірка: log3(2 – 4 + 1) = log39 = 2.
Відповідь: 4.
Приклад 2. Розв’яжіть рівняння log3x = log3(6 – х2).
Розв’язання
Із рівності логарифмів чисел випливає: х = 6 – х2; х2 + х – 6 = 0; х1 = -3, х2 = 2.
Перевірка:
1) Число -3 не є коренем даного рівняння, бо вираз log3(-3) – не визначений;
2) log3x = log32; log3(6 – х2) = log3(6 – 22) = log32.
Відповідь: 2.
Приклад 3. Розв’яжіть рівняння logх+1 (2х2 + 1) = 2.
Розв’язання
За означенням логарифма маємо:
2х2 + 1 = (х + 1)2; 2х2 + 1 = х2 + 2х + 1; х2 – 2х = 0; х1 = 0, х2 = 2.
Перевірка:
1) Значення х1 = 0 не є коренем даного рівняння, оскільки основа логарифма х + 1 не повинна дорівнювати 1.
2) logх+1(2-22 + l) = log39 = 2.
Відповідь: 2.
Відзначимо, що в описаних прикладах використовуються тільки такі перетворення, які не приводять до втрати коренів, але можуть привести до одержання сторонніх коренів. Тому перевірка кожного із одержаних коренів обов’язкова, якщо немає впевненості в рівносильності рівнянь.
Колективне розв’язування вправ № 53 (1; 3; 9), 54 (1), 52 (6; 13).
III. Підведення підсумків уроку
IV. Домашнє завдання
Розділ V § 3. Запитання і завдання для повторення розділу V № 26-29. Вправа № 52 (1-5).
(1 votes, average: 5.00 out of 5)
Loading...