ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ
Фізика підготовка до ЗНО комплексне видання
МЕХАНІКА
1. ОСНОВИ КІНЕМАТИКИ
1.2. ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ
Вектор – напрямлений відрізок. Векторні величини мають числове значення (модуль), напрям, точку прикладання (рис. 3).
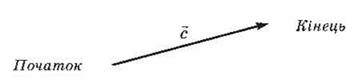
Рис. З
Проекція вектора 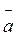 на вісь Ох – довжина відрізка, який сполучає проекцію початку вектора на вісь Ох з проекцією кінця вектора на ту саму вісь. Вона дорівнює добутку модуля
на вісь Ох – довжина відрізка, який сполучає проекцію початку вектора на вісь Ох з проекцією кінця вектора на ту саму вісь. Вона дорівнює добутку модуля
Цього вектора на косинус кута між напрямом осі та вектора.
Проекція вектора може бути додатною, від’ємною і дорівнювати нулю.
Якщо кут між напрямом вектора і віссю гострий, то 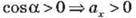 (рис. 4, а).
(рис. 4, а).
Якщо кут між напрямом вектора і віссю тупий, то 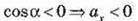 (рис. 4, б).
(рис. 4, б).
Якщо кут між напрямом вектора і віссю прямий 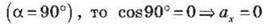 (рис. 4, в).
(рис. 4, в).
Модуль векторної величини можна визначити через проекції вектора на осі Ох і Оу (рис. 4, г):
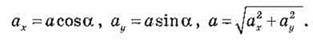
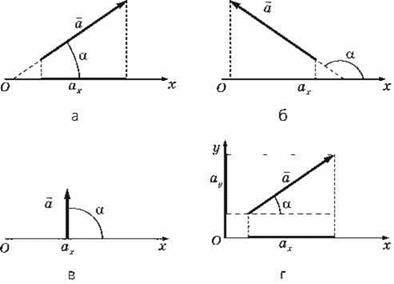
Рис. 4
При множенні векторної величини на скаляр одержуймо вектор, колінеарний даному:
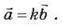
Додавання векторів за правилом трикутника: паралельним перенесенням суміщується початок другого вектора з кінцем першого, початок третього з кінцем другого і т. д.; тоді сума векторів – це вектор, що сполучає початок першого вектора з кінцем останнього.
На рис. 5, а зображено додавання двох векторів за правилом трикутника:
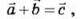
На рис. 5, б – додавання трьох векторів за правилом трикутника:
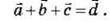
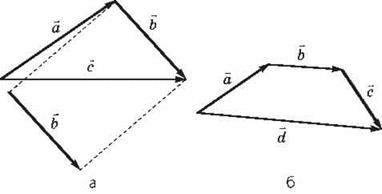
Рис. 5
Додавання векторів за правилом паралелограма: паралельним перенесенням суміщуються початки двох векторів; тоді сума векторів – діагональ, побудована на цих векторах як на сторонах паралелограма.
На рис, 6, а показано додавання двох векторів за правилом паралелограма, на рис. 6, б – додавання трьох векторів за правилом паралелограма.
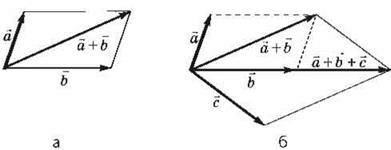
Рис. 6
Віднімання векторів за правилом трикутника: суміщуються початки двох векторів; тоді різниця векторів – це вектор, що з’єднує їхні кінці. Він напрямлений у бік зменшуваного вектора.
На рис. 7 показано віднімання двох векторів за правилом трикутника:
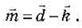
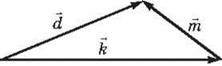
Рис. 7
Проекція суми векторів на координатну вісь дорівнює сумі проекцій складових векторів на ту саму вісь (рис. 8):
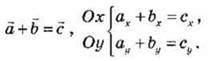
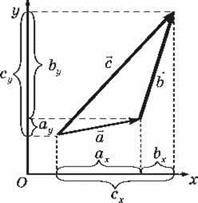
Рис. 8