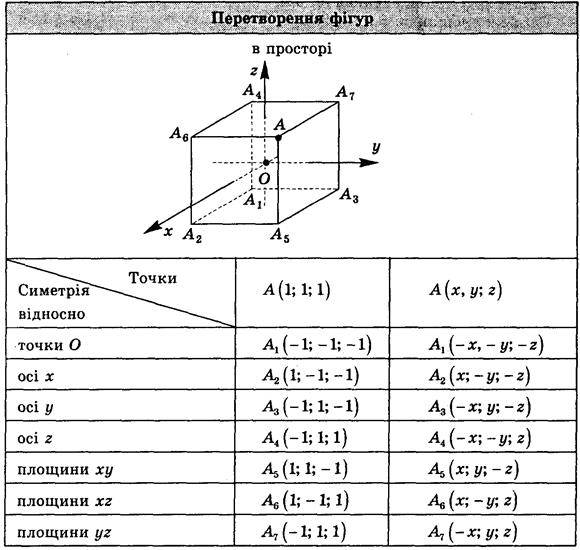
Перетворення симетрії в просторі. Симетрія в природі і на практиці
Урок 47
Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці
Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач.
Обладнання: схема “Перетворення фігур”.
Хід уроку
І. Перевірка домашнього завдання
1. Усне коментування розв’язування домашніх завдань.
2. Математичний диктант.
Дано трикутник АВС:
Варіант 1 – А (2; 0; 2), В (2; 2; 0), С (0; -2; 2);
Варіант 2 – А (2; 0; 0), В (2; – 2; 2), С (0; – 2; 0).
Точки K, L, M – середини сторін
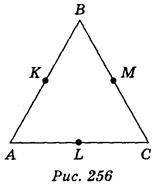
Користуючись зображенням, запишіть:
1) координати точки К; (2 бали)
2) координати точки L; (2 бали)
3) координати точки М; (2 бали)
4) довжину середньої лінії KL; (2 бали)
5) довжину медіани AM; (2 бали)
6) координати точки D, якщо чотирикутник ABCD – паралелограм. (2 бали)
Відповідь. Варіант 1. 1) К (2; 1; 1); 2) L (1; -1; 2); 3) M(1; 0; 1); 4) KL =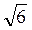 
; 5) AM = 
; 6) D(0; -4; 4).
Варіант 2. 1) К (2; – 1; 1) ; 2) L(1; -1; 0); 3) M(1; -2; 1); 4) KL =; 5) АМ = 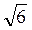; 6) D(0; 0; -2).
Означення симетрії відносно точки, відоме з планіметрії, залишається
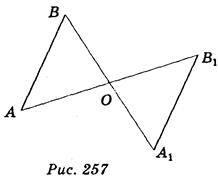
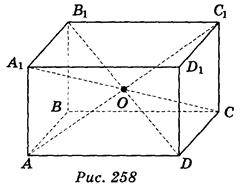
Точки А і А, називаються симетричними відносно точки О, якщо точка О – середина відрізка AA1. Перетворення, при якому кожна точка даної фігури відображається на точку, симетричну їй відносно точки О, називається симетрією відносно точки О, або центральною симетрією. На рис. 257 відрізок АВ при симетрії відносно точки О переходить у відрізок A1B1. Якщо симетрія відносно деякої точки О відображає дану фігуру на ту саму фігуру, таку фігуру називають центрально-симетричною, а точку О – її центром симетрії. Наприклад, центрально-симетричною фігурою є прямокутний паралелепіпед, точка перетину його діагоналей – центр симетрії (рис. 258).
1. Дано точку А (і; 2; 3). Знайдіть координати точки А1, симетричної точці А відносно початку координат. (Відповідь. А1(-1;-2;-3))
2. Точки А (5; -3; 4) і В(-3; 1; – 2) симетричні відносно точки С. Знайдіть координати точки С. (Відповідь. С(1; -1; 1))
3. Точка А (1; 2; 3) симетрична точці В відносно точки С(3; 2; 1). Знайдіть координати точки В. (Відповідь. В (5; 2; -1))
4. Чи симетричні будь-які дві точки простору відносно деякої третьої точки?
5. Скільки центрів симетрії має:
А) відрізок;
Б) пряма;
В) коло;
Г) площина;
Д) куб?
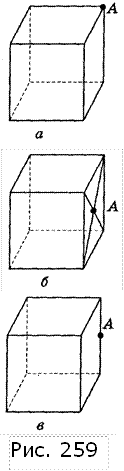
6. Дано куб. Побудуйте від руки фігуру, симетричну кубу відносно точки А (рис. 259).
Точки А і А1 називаються симетричними відносно прямої l, якщо пряма l проходить через середину відрізка АА1 і перпендикулярна до нього (рис. 260).
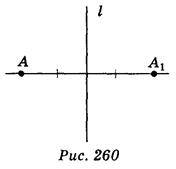
Перетворення, яке відображає кожну точку фігури на точку, симетричну їй відносно даної прямої, називається симетрією відносно прямої (або осьовою симетрією).
Розв’язування задач
1. Дано точку А (1; 2; 3). Знайдіть координати точки, симетричної їй відносно осі: а) х; б) у; в) z.
(Відповідь. Аx(1;-2;-3); Аy(-1; 2;-3); Аz(-1; -2; 3).)
2. Що таке вісь симетрії?
3. Скільки осей симетрії має:
А) відрізок;
Б) пряма;
В) коло;
Г) площина;
Д) куб.
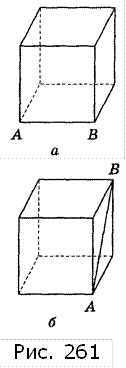
4. Дано куб. Побудуйте від руки фігуру, симетричну кубу відносно прямої АВ (рис. 261).
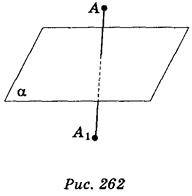
Точки А і A1 називаються симетричними відносно площини?, якщо ця площина перпендикулярна до відрізка АА1 і ділить його пополам (рис. 262). Перетворення, при якому кожна точка даної фігури відображається на точку, симетричну їй відносно площини?, називається симетрією відносно площини?. Якщо перетворення симетрії відносно площини а переводить фігуру в себе, то фігура називається симетричною відносно площини?, а площина? називається площиною симетрії.
Розв’язування задач
1. Задача № 17 із підручника (с. 55).
2. Скільки площин симетрії має:
А) відрізок;
Б) пряма;
В) коло;
Г) площина;
Д) куб?
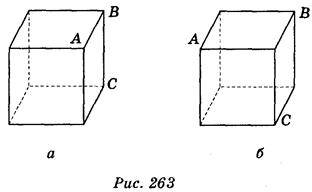
3. Дано куб. Побудуйте від руки фігуру, симетричну кубу відносно площини АВС (рис. 263).
III. Домашнє завдання
§4, п. 26, 27; контрольні запитання № 4, 5; задачі № 16, 18 (с. 55).
Підведення підсумку уроку можна провести з використанням поданої нижче схеми.
1) Що таке перетворення симетрії відносно точки?
2) Що таке перетворення симетрії відносно прямої?
3) Що таке перетворення симетрії відносно площини?
(1 votes, average: 5.00 out of 5)
Loading...