Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій
Урок 31
Тема. Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій
Мета уроку: формування понять: перпендикуляр до площини, похила, основа похилої, основа перпендикуляра, проекції похилої на площину, відстань від точки до площини. Виявлення взаємозв’язку між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій.
Обладнання: стереометричний набір.
Хід уроку
1. Два учні відтворюють на дошці розв’язання задач № 14, 15.
2. Розв’язування
1) Дано площину?, перпендикулярну до неї пряму а і іншу пряму b, яка не лежить в площині?. Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) якщо b || a, то b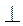
?;
Б) якщо b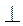?, то b || а ;
В) якщо b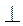?, то а і b мимобіжні;
Г) якщо b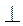?, то а і b перетинаються.
2) Дано площину?, паралельну їй пряму а і деяку пряму b, яка не лежить в площині?. Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) якщо b || a, то обов’язково b || ?;
Б) якщо b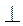?, то обов’язково
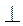А;В) якщо b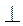? і b перетинає а, то b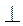А;
Г) якщо b?, то b і а обов’язково мимобіжні.
3. Обговорення правильності виконання учнями задач № 14, 15.
Перпендикуляр і похилі, взаємозв’язок між довжинами похилих. проведених з однієї точки, і довжинами їх проекцій
Перпендикуляром, опущеним з даної точки на дану площину, називають відрізок прямої, перпендикулярної до площини, що міститься між даною точкою і площиною.
На рис. 162 пряма AC перпендикулярна до площини? і перетинає її в точці С, отже, відрізок AC – перпендикуляр, опущений з точки А на площину?. Кінець цього відрізка, який лежить у площині, тобто точка С, називається основою перпендикуляра.
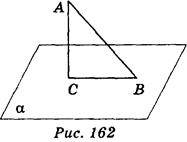
Якщо AC – перпендикуляр до площини?, а точка В – відмінна від С точка цієї площини, то відрізок АВ називають похилою, проведеною з точки А на площину?. Точка В – основа похилої. Відрізок, що з’єднує основи перпендикуляра і похилої, проведених з однієї і тієї самої точки, називається проекцією похилої. На рис. 162 відрізок ВС – проекція похилої АВ на площину?.
Прикладами матеріальних моделей перпендикулярів є: стовпи, телевізійні вежі тощо.
1. Знайти довжину похилої, якщо довжина перпендикуляра дорівнює 4 см, а проекція похилої на площину – 3 см.
2. Знайти проекцію похилої на площину, якщо похила дорівнює 13 см, а перпендикуляр, проведений з тієї ж точки,- 12 см.
3. Знайти довжину перпендикуляра, якщо похила дорівнює 10 см, а її проекція на площину – 8 см.
4. Скільки перпендикулярів можна опустити з даної точки до даної площини? Чому?
5. Скільки похилих можна провести з даної точки до даної площини?
6. Як слід установити на хрестовині ялинку, щоб вона була перпендикулярна до площини підлоги?
7. Як на практиці за допомогою виска перевірити вертикальність встановленого стовпа?
Слід зазначити, що перпендикуляр, опущений з точки, коротший за будь-яку похилу, проведену через дану точку.
Відстанню від точки до площини називається довжина перпендикуляра, опущеного з цієї точки на площину.
1. Знайти відстань від точки А до граней куба, якщо ребро куба дорівнює 10 см (рис. 163).
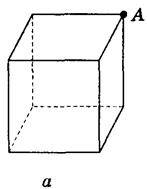
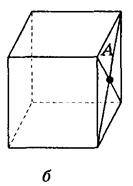
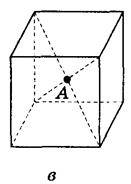
Рис. 163
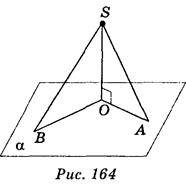
2. Із точки S проведено до площини а перпендикуляр SO та похилі SA і SB. Довжини похилих відповідно дорівнюють 13 і 20 см. Довжина проекції похилої AS дорівнює 5 см (рис. 164). Знайти відстань від точки S до площини та довжину проекції похилої SB.
Вивчення взаємозв’язку між довжинами похилих, проведених з однієї точки, і довжинами їх проекції доречно провести шляхом розв’язування задач.
Задача.
Із деякої точки проведено до площини дві похилі і перпендикуляр. Доведіть, що якщо:
1) похилі рівні, то рівні і їх проекції;
2) проекції похилих рівні, то рівні і похилі.
3) похилі нерівні, то більша похила має більшу проекцію.
Нехай АВ? (рис. 165); AC і AD – похилі; AC > BD.
Із? AСВ AC =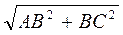 
.
Із? АDB AD =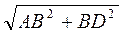 
.
Згідно з умовою AC > AD, тоді
> ;
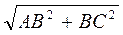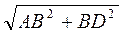АВ2 + ВС2 > АВ2 + BD2, або ВС2 > BD2; отже, ВС > BD.
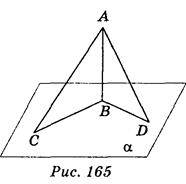
4) Доведіть: якщо похилі нерівні, то більшій проекції відповідає більша похила.
III. Закріплення та осмислення знань учнів
1. Задача № 22 із підручника (с. 36).
2. Задача № 23 із підручника (с. 36).
Нехай АВ? (рис. 165); AC = 17 cm, AD = 10 cm, СB – BD = 9 cm. Нехай BD = x cm, тоді CB = (x + 9) cm.
Із? АВD: АВ2 = AD2 – BD2 = 100 – x2.
Із? АСВ: АВ2 = AC2 – BC2 = 289 – (x+ 9)2. Тоді 100 – x2 = 289 – (x + 9)2; 100 – x2 = 289 – x2 – 18x – 81; 18x = 108; x = 6.
Отже, BD = 6 cm, CB = 6 + 9 = 15 (см).
Відповідь. 6 см і 15 см.
3. Задача № 25 із підручника (с. 36).
Розв’язання
Нехай АВ? (рис. 165); AD = 23 см, AC = 33 см, BD : CB = 2 : 3.
Нехай BD = 2x см, CB = 3х см. Із? АВD: АВ2 = AD2 – BD2 = 232 – 4×2.
Із? АВС: АВ2 = AC2 – BC2 = 332 – 9×2. Тоді 232 – 4×2 = 332 – 9×2;
5×2 =332 – 232; 5×2 = (33 – 23)(33 + 23); x2 =112 і АВ =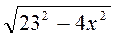 
= 
= 
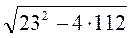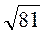= 9 (см). Отже, довжина перпендикуляра дорівнює 9 см.
Відповідь. 9 см.
§3, п. 18; контрольні запитання № 7-9; задача № 24 (с. 36).
V. Підведення підсумку уроку
Запитання до класу
1) Що таке перпендикуляр, опущений з даної точки до площини?
2) Що таке похила, проведена з даної точки до площини?
3) Скільки перпендикулярів та похилих можна побудувати з даної точки до площини?
4) 3 даної точки до площини проведено дві похилі. Що можна стверджувати про проекції похилих на площину, якщо похилі:
А) рівні;
Б) не рівні?
(1 votes, average: 5.00 out of 5)
Loading...