Піраміди і зрізані піраміди
796.
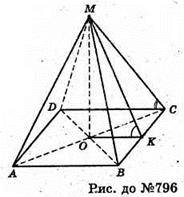
Нехай дано правильну чотирикутну піраміду, висота якої MO = 147 м,
А площа основи – SABCD = 5,3 га = 53 000 м2.
∠MCO – кут нахилу бічного ребра.
OK + ВС, MK + BC, ∠MKO – лінійний кут двогранного кута при ребрі основи піраміди. SABCD = 53 000 м2;
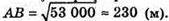
ΔMOK – прямокутний. ∠MOK = 90°;
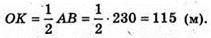
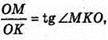
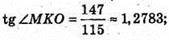∠ MKO = arctg 1,2783.
∠
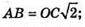
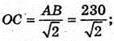
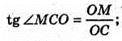
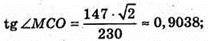
797.
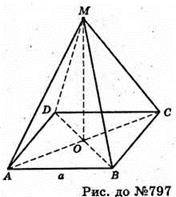
Нехай дано правильну чотирикутну піраміду MABCD.
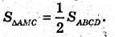
Нехай AB = а, тоді SABCD = а2;
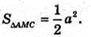
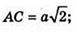
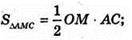
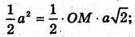
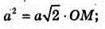
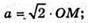
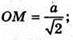
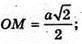
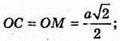
Δ MOC – прямокутний рівнобедрений.
∠OMC = ∠OCM = 45°, ∠AMC = 90°, що й треба було довести.
Отже, AM і MC – протилежні бічні ребра піраміди перпендикулярні.
798.
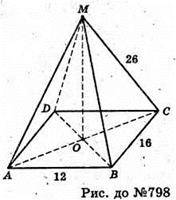
Нехай основа піраміди
Кожне бічне ребро дорівнює 26 см. AM = DM = CM = BM = 26 см.
Розглянемо ΔABC – прямокутний.
AC2 = AB2 + BC2 = 144 + 256 = 400; AC = 20 см;
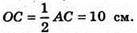
Δ MOC – прямокутний. OM2 = MC2 – OC2;
OM2 = 262 – 102 = 676 – 100 = 576;
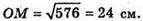
799.
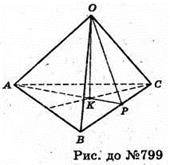
Нехай дано тетраедр ОАВС. Знайдемо довжини ребер.
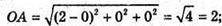
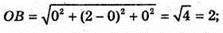
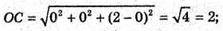
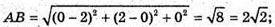
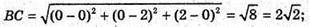
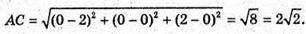
ΔABC – рівносторонній.
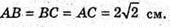
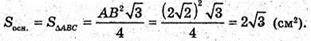
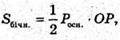
Де OP – висота бічної грані.
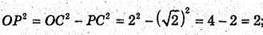
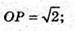
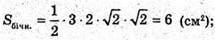
800.
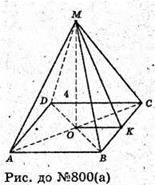
А) Нехай дано чотирикутну піраміду, в основі якої лежить
Квадрат зі стороною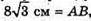 
MO = 4 см.
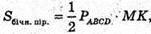де МK – висота бічної грані.
ΔMOK.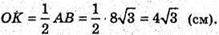 
MK2= MO2 + OK2 = 16 + 48 = 64. МK = 8 (см).
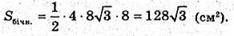
Б)
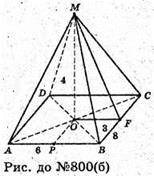
Нехай в основі піраміди лежить прямокутник зі сторонами 6 см і 8 см,
Висота піраміди MO = 4 см.
ΔMOF – прямокутний. MF2 = MO2 + OF2;
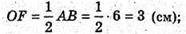
MF2 = 16 + 9 = 25; MF = 5 см.
Δ MOP – прямокутний.
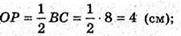
MP2 = MO2 + OP2 = 16 + 16 = 32;
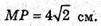
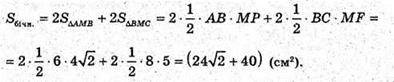
В)
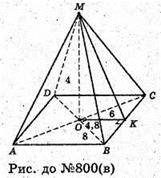
Нехай в основі піраміди лежить ромб з діагоналями 12 см і 16 см.
AC = 12 см, BP = 16 см.
ABCD – ромб. ΔBOC – прямокутний.
BC2= OB2 + OC2 = 64 + 36 = 100;
BC = 10 см. OK + BC, MK + BC.
OK – радіус кола, вписаного в основу.
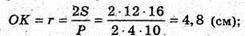
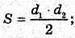
P = 4а. ΔMOK – прямокутний. MK2 = MO2 + OK2;
MK2 = 16 + 23,04 = 39,04.
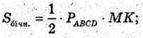
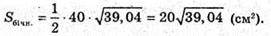
Г)
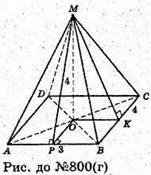
Нехай основа піраміди :- паралелограм ABCD,
Площа якого 24 см2 зі сторонами 3 см і 4 см.
Знайдемо висоти паралелограма.
S = а × h або S = b × h2.
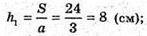
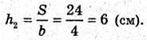
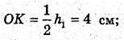
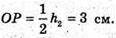
ΔΜΟΚ – прямокутний. MK2 = MO2 + OK2= 16 + 16 = 32;
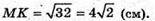
ΔMOP – прямокутний. MP2 = MO2 + OP2 = 16 + 9 = 25;
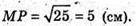
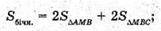
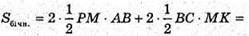
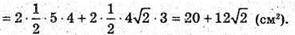
801.
А)
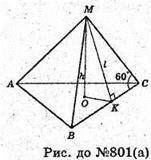
Нехай дано правильний тетраедр МАВС, в якому сторона основи
AB = BC = AC = a, AM = MB = MC = а.
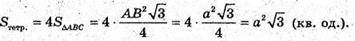
Б) Нехай апофема правильного тетраедра MK = l.
ΔMKC – прямокутний.
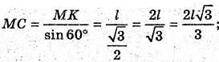
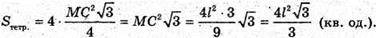
В) Нехай висота правильного тетраедра MO = h.
Нехай AB = BC = AC = а;
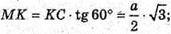
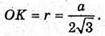
ΔMOK-прямокутний. MO2 + OK2 = MK2.
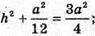
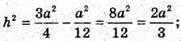
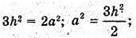
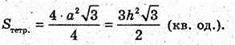
802.
А)
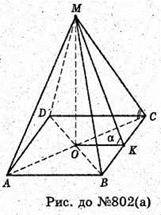
Нехай дана правильна чотирикутна піраміда, основа якої квадрат ABCD,
AB = BC =DC = AD = a. OM + (ABCD), OK + BC, тоді за теоремою про три перпендикуляри MK + BC, ∠MKO – лінійний кут двогранного кута при ребрі основи. ∠MKO = α. Sповерхні = Sб. + Socнови, Socнови = SABCD = AB2 = а2.
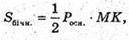Де Poсн. = 4АВ = 4а; MK – апофема.
Δ MOK – прямокутний.
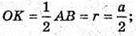
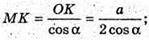
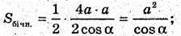
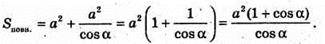
Б) Нехай висота піраміди MO = А, бічне ребро MC утворює з площиною основи ∠MCO = 45°. Sповерхні = Sбічн. + Sоснови
ΔMOC – прямокутний. OC = h × ctg ∠MCO = h × ctg 45° = h × 1 = А.
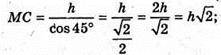
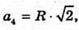де R = ОС,
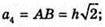Sосн. = a42 = 2A2.
ΔMKC – прямокутний.
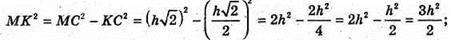
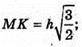
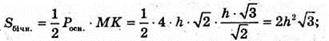
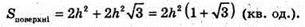
В)
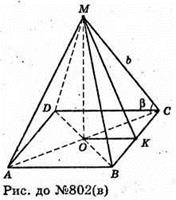
Нехай дано правильну чотирикутну піраміду, бічне ребро якої MC = b і утворює з площиною основи кут β. ∠MCO – β (кут між прямою і її проекцією на площину). ΔMOC – прямокутний. OC = b × cos β, OC – радіус кола, описаного навколо основи піраміди.
OK + ВС, OM + (ABCD), тоді за теоремою про три перпендикуляри MK + ВС. MK – апофема піраміди.
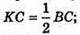
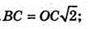
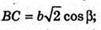
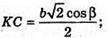
Socн = BC2b cos2β;
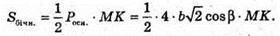
ΔMKC – прямокутний.
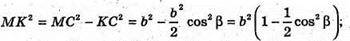
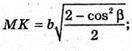
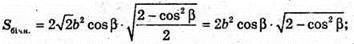
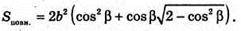
Г)
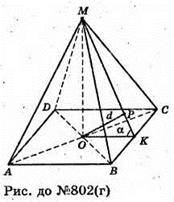
Нехай дано піраміду (правильна чотирикутна), відстань від основи висоти до бічної грані дорівнює d, OP = d, OK + ВС, MK + ВС, ∠MKO = α.
∠MKO – лінійний кут при ребрі основи піраміди.
ΔOPK – прямокутний.
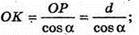
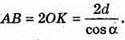
ΔMOK – прямокутний.
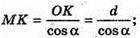
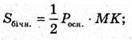
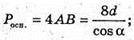
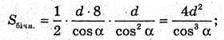
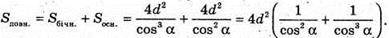
Г)
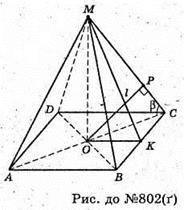
Нехай дано чотирикутну піраміду MABCD, в основі якої квадрат ABCD.
OP + МС, OP = l, OP – відстань від основи висоти до бічного ребра.
Бічне ребро MC утворює кут ∠MCO = β з площиною основи.
ΔMOC – прямокутний.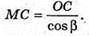 
ΔOPC – прямокутний. OP + МС.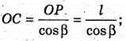 
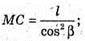
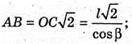
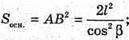
MK + ВС.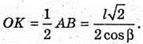 
ΔMOC – прямокутний. OM = OS × tg β.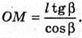 
ΔΜΟΚ – прямокутний.
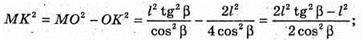
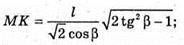
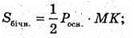
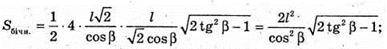
Sповерхні = Sбічн. + Sосн.
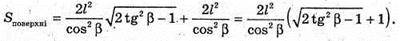
804.
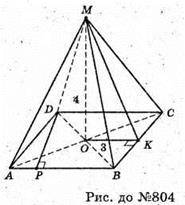
Нехай дано піраміду MABCD, в основі якої ромб ABCD, гострий кут якого
∠DAB = 45°, OK – радіус вписаного кола, OK = 3 см, OK + ВС, MO + (ABCD),
MO – висота піраміди. MO = 4 см.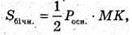 
де MK — висота бічної грані.
ΔMOK – прямокутний. MK2= MO2 + OK2 = = 16 + 9 = 25;
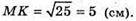OK = r: h = 2r;
H – висота основи, DP = h – висота ромба ABCD; h = 2 × 3 = 6 см.
ΔADP – прямокутний.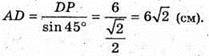 
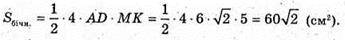
Відповідь: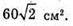 
805.
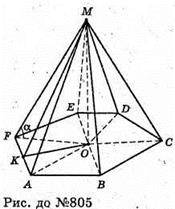
Нехай дано правильну шестикутну піраміду MABCDEF зі стороною основи
AB = а, бічне ребро FM нахилене до площини основи під кутом α = 45°.
∠MFO = α, кут між прямою і площиною, OK + FA, тоді за теоремою про три перпендикуляри MK + FA, MK – апофема піраміди.
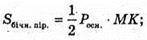Pocн. = 6AF = 6 × 7 = 42 (см).
ΔOFM – прямокутний. OF – радіус описаного кола навколо шестикутника.
OF = R = а6 = 7 см;
OM = OF × tg α = 7 tg 45° = 7 × 1 = 7 (см).
OK = r — радіус кола, вписаного в основу піраміди.
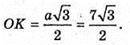
ΔMOK – прямокутний. ∠FOM = 90°.
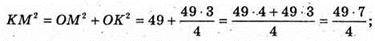
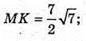
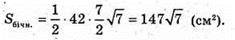
806.
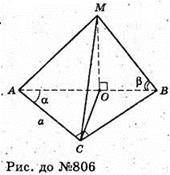
Нехай в основі піраміди лежить прямокутний трикутник ΔABC (∠ACB = 90°) з катетом AC – а, ∠CAB = α. Всі бічні ребра нахилені до площини основи під кутом β. ∠MBO = ∠MCO = ∠MAO = β. AO = OB = OC = R – радіус кола, описаного навколо основи піраміди. O – середина гіпотенузи.
MO + АВ, MO – висота піраміди.
ΔАВС.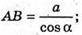 
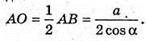
ΔAMO – прямокутний.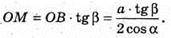 
Відповідь: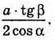 
807.
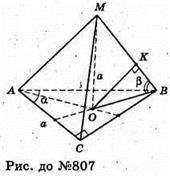
Нехай дано піраміду MABC, в основі якої лежить рівнобедрений трикутник (ΔАВС). AB =AC = a. ∠BAC = α. Всі бічні ребра піраміди нахилені до площини основи під кутом β. ∠MAO = ∠MBO = ∠MCO = β. ОK – відстань від основи висоти піраміди до її бічного ребра.
ΔАВС. BC = 2R × sin α = 2 × OB × sin α,
OB – радіус кола, описаного навколо ΔАВС.
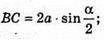
ΔАВС.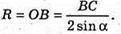 
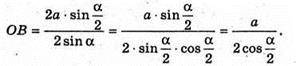
ΔOKB – прямокутний. OK + MB.
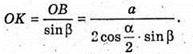
Відповідь: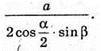 
808.
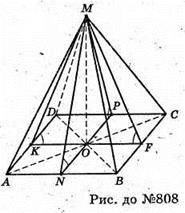
Нехай дано піраміду MABCD, у якої всі двогранні кути при ребрах основи піраміди рівні. ∠MFO = ∠MPO = ∠MNO = ∠MKO.
ΔMOF = ΔMOP = ΔMOK = ΔMON – прямокутні (за катетом і гострим кутом).
З їх рівності маємо: OF = OP = ON = ОK.
OF + ВС, OP + DC, OK + AD, ON + AB.
Точка O рівновіддалена від сторін основи піраміди.
Точка O – центр кола, вписаного в основу піраміди. Отже, якщо всі двогранні кути при ребрах основи піраміди рівні, то основа її висоти – центр кола, вписаного в основу піраміди.
809.
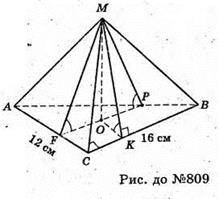
Нехай дано піраміду, в основі якої лежить прямокутний ΔABC з катетами
AC = 12 см, BC = 16 см, ∠ACB = 90°. MO + пл. ΔАВС. MO – висота піраміди.
OK + ВС, MK + ВС, OP + АВ, MP + АВ, OF + AC, MF + AC.
∠MPO = ∠MKO = ∠MFO – лінійні кути двогранних кутів при ребрах основи піраміди. ∠MFO = ∠MPO = ∠MKO = 60°.
O – центр кола, вписаного в основу піраміди, OF = OP = OK = г – радіус кола, вписаного в основу піраміди.
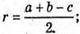а = 12 см, b = 16 см,
С2 = а2 + b2 = 122 + 162 = 144 + 256 = 400; с = 20 см.
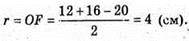
ΔMOF – прямокутний.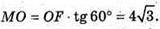 
Відповідь: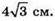 
810.
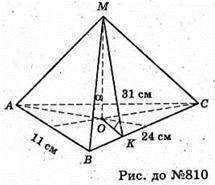
Нехай дано піраміду MABC, в основі якої лежить ΔABC зі сторонами AB = 11 см, BC = 24 см, AC = 31 см. MO + пл. ΔАВС. MO – висота піраміди. MO = 2 см.
MO + пл. ΔАВС, OK + ВС, MK + ВС. ∠MKO – лінійний кут двогранного кута при ребрі ВС.
Усі двогранні кути при ребрах основи рівні, отже, O – центр кола, вписаного в основу піраміди,
OK – радіус цього кола. OK = г; де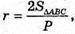 
SΔABC – площа основи піраміди, P – периметр основи піраміди.
P = 31 + 24 + 11 = 66 (см).
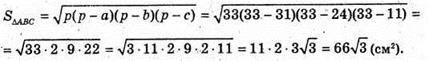
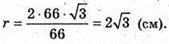
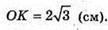
Знайдемо ∠MKO.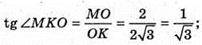 
∠MKO = 60°.
Відповідь: 60°.
811.
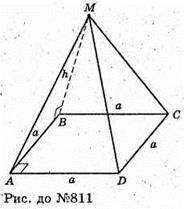
Нехай дано піраміду MABCD, основа якої квадрат ABCD,
AB = BC = CD = AD = a. MB + пл. ABCD. MB = h, MB – висота піраміди.
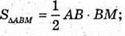
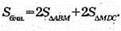
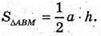
ΔMBA – прямокутний, ∠MBA = 90°.
MB + (ABCD), AB + AD, за теоремою про три перпендикуляри AM + AD,
ΔMAD – прямокутний, ∠MAD = 90°,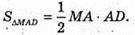 
ΔMAB – прямокутний. AB2 = MB2 + AB2 = h2+ а2;
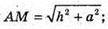
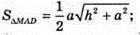
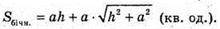
812.
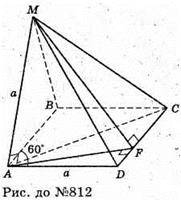
Нехай дано MABCD – .піраміда, в основі якої лежить ромб ABCD, сторона ромба AB = BC = DC = AD = a. ∠BAD = 60°, MA + пл. ABCD. MA = а. MA – висота піраміди.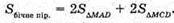 
ΔMAD – прямокутний.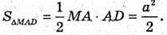 
Проведемо AF + DC, тоді за теоремою про три перпендикуляри MF + DC.
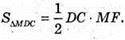
ΔAFD – прямокутний.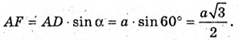 
ΔMAF – прямокутний.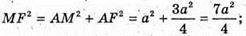 
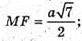
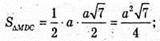
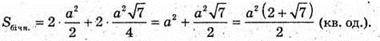
Відповідь: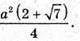 
813.
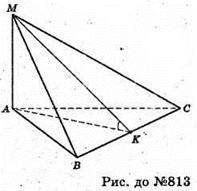
Нехай дано піраміду, в основі якої лежить правильний ΔABC.
Грань МАВ + площині ABC. Грань МАС + площині (ABC). AK + ВС, MK + ВС, ∠MKA = 30°. ∠MKA – кут нахилу грані MBC до площини (ΔАВС).
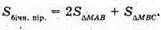
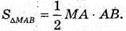
ΔMAB – прямокутний. MA + (ABC), MA + АВ.
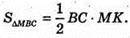Нехай AB = AC = BC = а, тоді
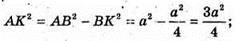
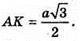
ΔMAK – прямокутний.
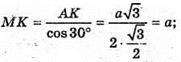
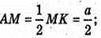
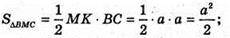
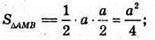
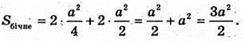
Відповідь: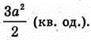 
814.
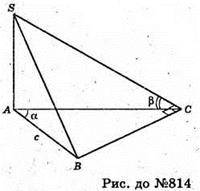
Нехай дано піраміду SABC, в основі якої лежить прямокутний ААВС,
У якого ∠C = 90°, ∠A = α, AB = с. Грань SAB і грань SAC перпендикулярні до площини основи ΔАВС.
AC + ВС, тоді за теоремою про три перпендикуляри SC + BC, отже, ∠SCA = β, ∠SCA – лінійний кут двогранного кута, який утворює грань SCB з площиною основи.
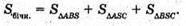
ΔАВС – прямокутний. BC = ctg α;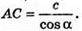 
ΔSAC – прямокутний.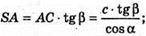 
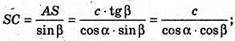
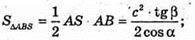
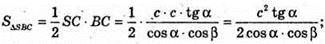
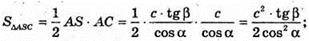
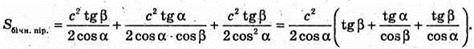
Відповідь: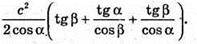 
815.
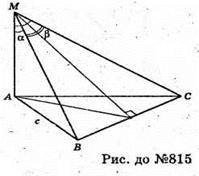
Нехай дано трикутну піраміду МАВС, у якої ∠BMA = ∠CMA = α, ∠BMC = β, а, а, β – плоскі кути при вершині піраміди. MA – бічне ребро – спільна сторона рівних кутів. MA + площині ΔABC, MA + AC, MA + АВ. AM = а.
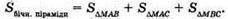
ΔМАВ = ΔMAC (за катетом і гострим кутом).
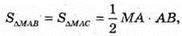
AB = a tg α.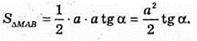 
AF + BC, MF + ВС, MF – висота ΔМВС.
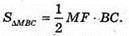
ΔAMВ.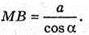 
ΔMBC – рівнобедрений. MC = MB; BF = FC.
ΔMBF.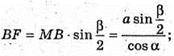 
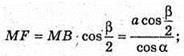
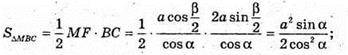
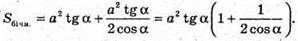
Відповідь: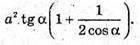 
816.
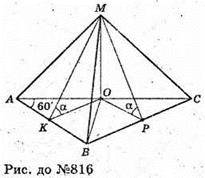
Нехай дано піраміду, в основі якої лежить правильний ΔАВС. AB = BC = AC = а.
Грань МАС перпендикулярна до площини основи. MO + (ABC), MO + AC, MO – висота піраміди. OK + AB, MK = AB, ∠MKO = α, ∠MKO – кут нахилу бічної грані AMB до площини основи. OP + BC, MP + ВС. ∠MPO = α, ∠MPO – кут нахилу грані MBC до площини основи. ∠MKO = ∠MPO = α.
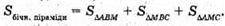
ΔAOK – прямокутний.
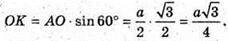
ΔMOK – прямокутний.
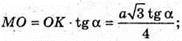
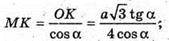
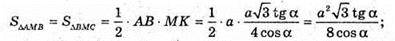
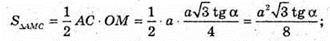
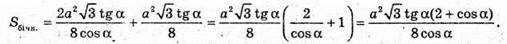
Відповідь: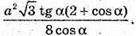 
817.
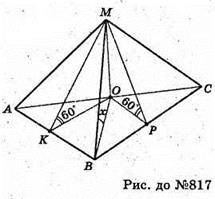
Нехай дано трикутну піраміду, в основі якої лежить правильний ΔАВС.
AB = BC = AC. Бічна грань AMC перпендикулярна до площини основи.
MO + ABC, MO + AC. MO + ABC, ОK + АВ, MP + BC, OK + AB, MK + AB,
∠MPO = ∠MKO = 60°. ∠MPO і ∠MKO – лінійні кути нахилу граней
MBC і МАВ до площини основи.
MB – найбільше бічне ребро, тому що його проекція OB більша,
Ніж проекції AM і MC. Нехай AB = BC = AC = а.
ΔAOK – прямокутний. ∠KAO = 60°,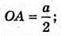 
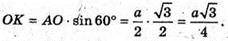
ΔMOK – прямокутний. ∠MOK = 90°,
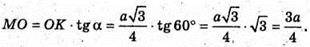
ΔAOB – прямокутний. ∠AOB = 90°,
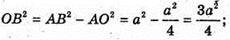
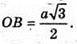
ΔMOB – прямокутний.
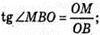
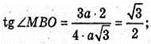
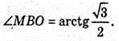
Відповідь: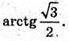 
818.
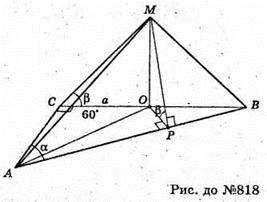
Нехай дано піраміду, в основі якої прямокутний трикутник з кутом а. ∠CAB = α. BC = а. Грань MCB проходить через катет BC = а і перпендикулярна до площини основи. Грань MCA нахилена до площини основи під кутом ∠MCB = φ. BC + АС, МО + ABC, тоді MC + АС. Грань МАВ нахилена до площини основи під кутом ∠MPO = φ. MO + ABC, OP + AB, тоді MP + АВ. MO – висота піраміди. ΔMOC = ΔMOP – прямокутні. OM – спільна сторона – ∠MPO = ∠MCO = φ.
З їх рівності маємо: OC = ОР.
ΔCOP – ΔPOA – прямокутні (за двома катетами).
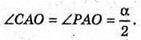
З ΔCAO: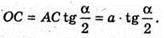 
ΔMOP – прямокутний.
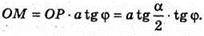
Відповідь: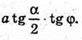 
819.
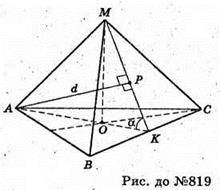
Нехай дано правильну трикутну піраміду. Вершина А знаходиться на відстані AP = d від протилежної грані BMC. У площині (AMK) MK – апофема піраміди.
Проведемо AP + МK. OK + BC, MK + BC, отже, ∠MKO – лінійний кут двогранного кута при ребрі основи піраміди.
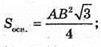
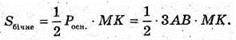
ΔAPK – прямокутний.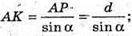 
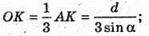
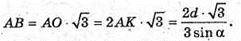
ΔMOK – прямокутний.
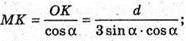
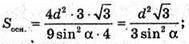
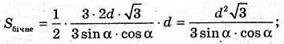
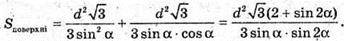
820.
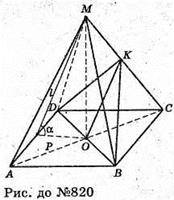
Нехай дано правильну чотирикутну піраміду MABCD, в основі якої
Лежить квадрат ABCD. Бічна грань утворює з площиною кут ∠MPO = α.
OP + AD, MP + AD. MP = l, MP – апофема піраміди, Через діагональ BD основи піраміди проведемо переріз DKB паралельно ребру AM.
В площині (AMC) проведемо OK? AM.
Переріз піраміди ΔDKB – рівнобедрений, DK = BK (за умовою піраміда правильна).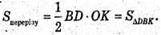 
ΔMPO – прямокутний. MO = MP × sin α = l sin α.
OP = MP × cos α; OP = I cos α. AB = 2OP = 21 cos α;
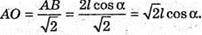
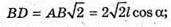
ΔAMO – прямокутний. AM2= OM2 + AO2;
AM2 = l2 sin2α + 2l cos2α = l2(sin2 α + 2 cos2α).
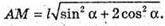
ΔAMC. OK – середня лінія ΔАМС. OK? AM, AO = ОС, тоді за теоремою Фалеса
MK = KC.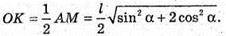 
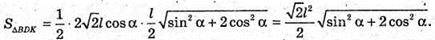
Відповідь: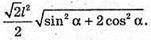 
821.
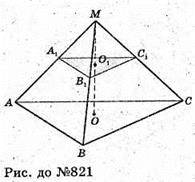
Нехай дано піраміду МАВС, висота MO = 12 см, площа основи SΔBCD = 288 см2, SΔB1C1D1 = 50 см2. Піраміда MA1B1C1подібна до піраміди МАВС.
Проведемо переріз площиною (A1B1C1) паралельно площині (ABC).
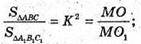MO1 = x;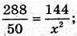 
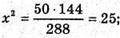
X = 5, MO1 = 5, OO1 = OM – O1M = 12 – 5 = 7 (см).
Відповідь: 7 см.
822.
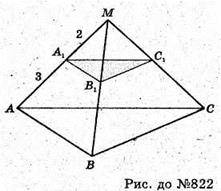
Нехай дано піраміду MABC. Паралельно основі піраміди проведемо переріз A1B1C1. AA1 : A1M = 3 : 2. SΔABC більша SΔA1B1C1 на 63 см2.
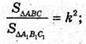
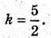
Нехай SΔA1B1C1 = х, тоді SΔABC = x + 63.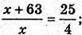 
4х + 252 = 25х; 21x = 252; x = 12; S ΔABC = 12 + 63 = 75 (см2).
Відповідь: 75 см2.
823.
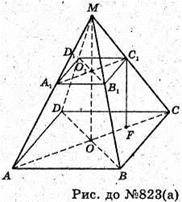
Нехай дано зрізану правильну чотирикутну піраміду, висота якої OO1 = 12 см, AB = BC = CD = AD = 38 см, A1B1 = B1C1= D1C1 =A1D1 = 20 см.
A) C1C – бічне ребро; C1F + AC, C1F – висота піраміди.
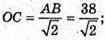
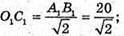
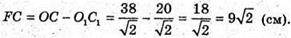
ΔC1CF – прямокутний.
C1C2 = C1F2 + FC2 = 144 +162 = 306;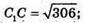 
Б) AA1C1C – переріз, який проходить через діагоналі основ.
AA1C1C – трапеція.
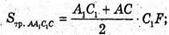
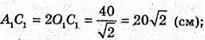
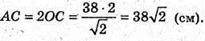
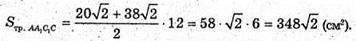
В)
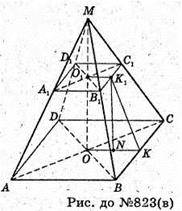
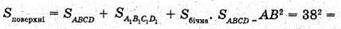
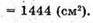
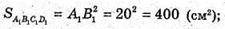
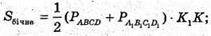
OK = r – радіус кола, вписаного кола в нижню основу.
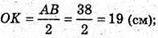
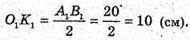
NK = OK – O1K1= 19 – – 10 = 9 (см).
AK1NK – прямокутний.
K1K2 = B1N2 + NK2; K1K2 = 122 + 92 = 144 + 81 = 225;
K1K = 15 (см).
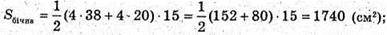
Sповерхні = 1444 + 400 + 1740 = 3584 (см2).
824.
А)
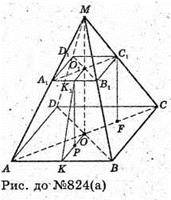
Нехай дано зрізану правильну чотирикутну піраміду. Сторони основ дорівнюють: AB = BC = DC = = AD = 12 см; A1B1 = B1C1 = B1C1 = A1B1- 8 см,
C1C нахилена до площини основи під кутом ∠C1CO = 60°.
K1K – апофема.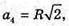 
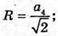
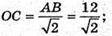
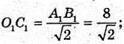
C1F + ОС;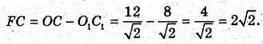 
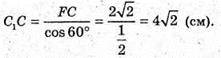
ΔC1FC – прямокутний.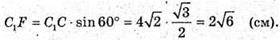 
OK = r.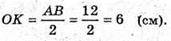 
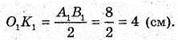
K1B + OK; PK = OK – O1K1 = 6 – 4 = 2 (см).
ΔK1KP – прямокутний.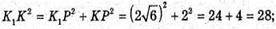 
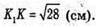
Відповідь: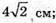 
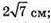
Б) Нехай дано зрізану правильну трикутну піраміду, сторони основ якої дорівнюють: AB = BC = AC = 12 см; A1B1 = B1C1 = A1C1 = 8 см.
OC і O1C1 – радіуси кіл, описаних навколо основ.
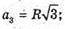
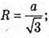
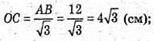
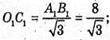
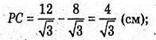
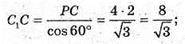
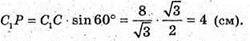
C1C – бічне ребро. K1K – апофема.
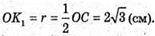
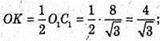
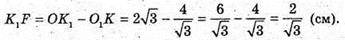
ΔKK1F – прямокутний.
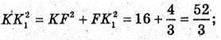
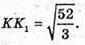
В)
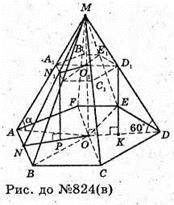
Нехай дано зрізану шестикутну піраміду. a6 = R; OD = R = AB = 12 см,
O1D1- A1B1 = 8 см; KD = OD – O1D1 = 12 – 8 = 4 (см).
ΔD1KD – прямокутний.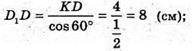 
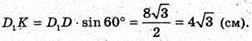
NN1- апофема.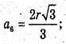 
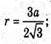
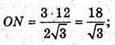
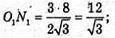
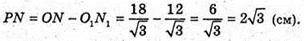
ΔNN1P – прямокутний.
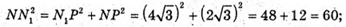
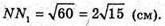
825.
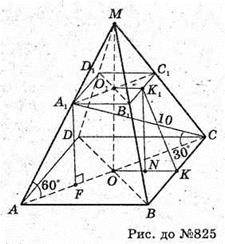
Нехай дано правильну чотирикутну зрізану піраміду, діагональ якої дорівнює 10 см; A1C = 10 см; ∠A1CA = 30° (кут між прямою A1C і площиною ABCD).
∠A1AO – 60°.
ΔA1CA — прямокутний. ∠A = 60°; ∠C = 30°;
∠A1 = 90°;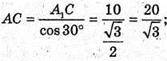
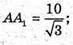
A1F + AC; A1F = AA1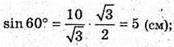 
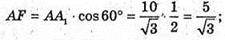
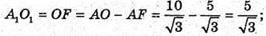
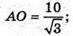
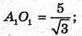
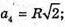
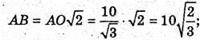
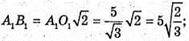
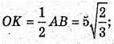
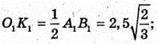
K1N + OK;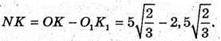 
AK NK – прямокутний. KK2 = K1N2 + NK2;
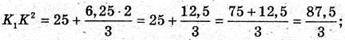
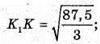
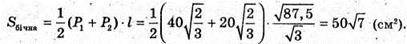
826.
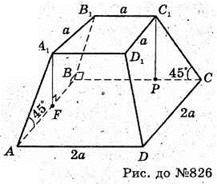
Нехай дано зрізану піраміду, основою якої е квадрат ABCD. Дві бічні грані A1B1BA і B1BCC1 перпендикулярні до площини основи, а дві інші утворюють з нею кут 45°. Сторона нижньої основи AB = BC = DC = AD = 2а. Сторона верхньої основи A1B1 = B1C1 = C1D1=A1D1 = а.
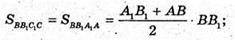
AB = 2а; A1B1= a; A1F + АВ; ΔA1FA – прямокутний.
A1F = FA =2а – а = а.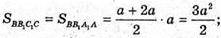 
C1P + DC; PC + DC, тоді C1C + DC.
ΔC1PC – прямокутний.
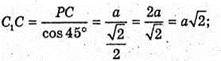
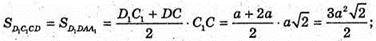
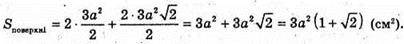
827.
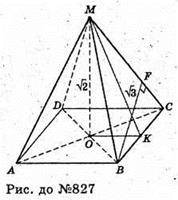
Нехай дано правильну чотирикутну піраміду MABCD, висота якої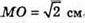 
А висота бічної грані, проведена до бічного ребра, дорівнює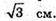 
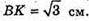
Нехай OC = х, тоді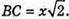 
ΔMOC – прямокутний. MC2= MO2 + OC2- 2 + x2;
MF + BC,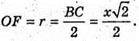 
ΔMOF.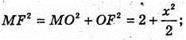 
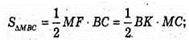
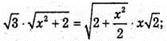
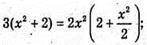
Зх2 + 6 = 4х2 + x4; х4 + x2- 6 = 0. Нехай х2 = t, t > 0. t2 + t – 6 = 0; t1 = -3; t2 = 2.
X2 = 2; MC2= 2 + 2 = 4; MC = 2.
Відповідь: MC = 2.
828.
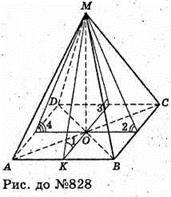
Нехай дано піраміду, основою якої є квадрат. OK + AD, MK + AD.
∠MKO – лінійний кут двогранного кута при ребрі основи.
∠1 : ∠2 : ∠3 : ∠4 = 1 : 2 : 4 : 2.
Відповідь: 30°, 60°, 120°, 60°.
829.
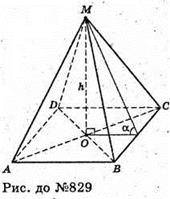
Нехай дано правильну чотирикутну піраміду, у якої висота MO = h, а двогранний кут при бічному ребрі α. OK + ВС, MK + ВС. ∠MKO = α.
ΔMOK – прямокутний. OK = OM × ctg α = h ctg α; AB = 2OK = 2h ctg α.
Sоснови = AB2 = 4h2 ctg2α.
Відповідь: 4h2 ctg2α.
830.
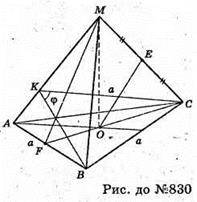
Нехай дано трикутну правильну піраміду. Відстань від основи висоти OM до середини E бічного ребра MC дорівнює стороні основи. OE = AB.
BK + AM, KC + AM, ∠ BKC = φ, кут між суміжними бічними гранями.
ΔMOC – прямокутний. ME = OE = EC = a; MC = 2а.
ΔAMF – прямокутний.
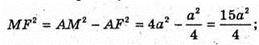
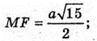
AM × BK = AB × MF;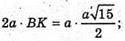 
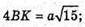
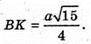
ΔВКС. За теоремою косинусів маємо: BC2 = BK2 + KC2 – 2ВК × KC × cos ∠K;
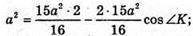
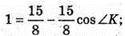
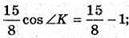
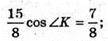
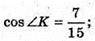
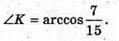
Відповідь: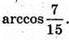
831.
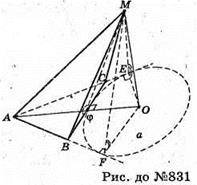
Нехай дано піраміду МАВС, основа якої – правильний трикутник ABC. Основа висоти MO проходить через один із центрів O зовнівписаного кола. Висота MO дорівнює радіусу кола, тобто MO = OF = OE = OP = R. OF + AB; MF + AB.
∠MFO – лінійний кут двогранного кута при ребрі основи. OE + AC; ME + AC.
∠MEO – лінійний кут при ребрі основи. OP + BC; MP + PO.
∠MPO – суміжний кут двогранного кута при ребрі основи.
∠MPO = 135°; ∠MFO = ∠MEO =45°.
ΔMOF – прямокутний. MO = OE = R.
Відповідь: 45°; 45°; 135°.
832.
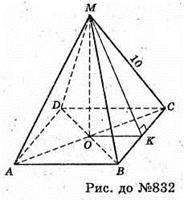
Нехай дана правильна чотирикутна піраміда, бічне ребро якої 10 см, площа повної поверхні 64 см 2. MC = MB = MA = MD = 10 см.
Нехай AB = BC = DC = AD = х, тоді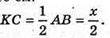 
ΔMKC – прямокутний. OM + (ABCD), OK + BC. За теоремою про три перпендикуляри MK + BC. За теоремою Піфагора: MK2 = MC2- KC2;
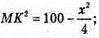
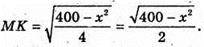
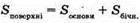
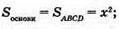
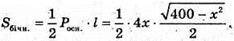
За умовою площа повної поверхні 64 см2.
Складемо рівняння: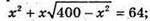 
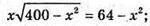
Х2(400 – x2) = 4096 – 128х2 + х4; 400х2 – х4 = 4096 – 128х2 + x4;
-2х4 + 528х2 – 4096 = 0; x4 – 264х2 + 2048 = 0.
Нехай x2 = t, t > 0. t2- 264t + 2048 = 0;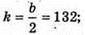 
D1 = k2- ас = 17 424 – 2048 = 15 376;
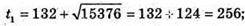
T2 = 132 – 124 = 8; x2 = 256 або x2 = 8;
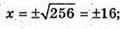
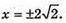
Відповідь: 16 см або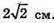 
833.
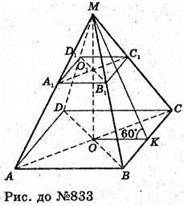
Нехай MABCD – правильна чотирикутна піраміда, двогранні кути при основі піраміди дорівнюють 60°. ∠MKO = 60°. A1B1C1D1 – переріз, який проведений паралельно основі піраміди і ділить висоту у відношенні MO1·. OO1 = 1 : 3.
Нехай AB = х, тоді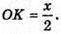
З ΔМОK: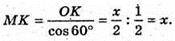 
Площа основи: SABCD = х2.
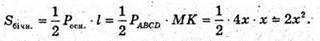
Площа повної поверхні 192 см2.
X2 + 2×2 = 192; 3×2 = 192; x2 = 96;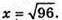 
Піраміда MA1B 1C1D1- MABCD,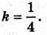 
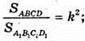
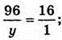у = 96 : 6; у = 6.
Нехай SA1B1C1D1 = y – площа перерізу.
Відповідь: 6 см2.
834.
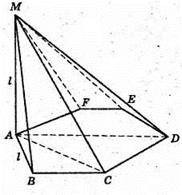
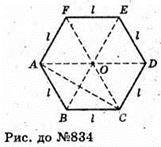
Нехай дано піраміду MABCDEF, в основі якої лежить правильний шестикутник
Зі стороною l, а одне з бічних ребер перпендикулярне до площини основи,
MA + (ABCDEF). MA = l.
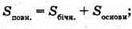
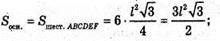
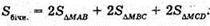
ΔMAB – прямокутний.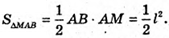 
ΔMAB – прямокутний. MB2 = MA2 + AB2 = 2l2;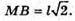 
ΔMAD – прямокутний. MD2 = MA2 + AD2 = I2 + 4l2 = 5l2; AD = 2R = 2l; а6 = R;
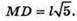
ΔABC – рівнобедрений. AB = BC;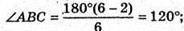 
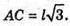
ΔMAC – прямокутний. MC2 = MA2 + AC2; MC2 = l2 + 3l2 = 4l2; MC = 2l.
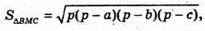де
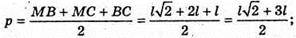
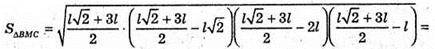
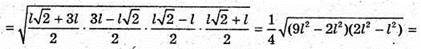
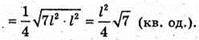
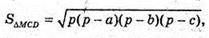
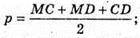
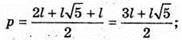
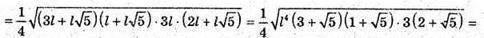
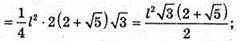
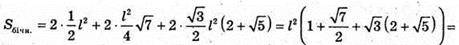
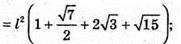
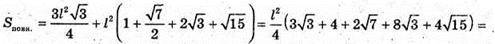
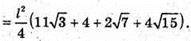
835.
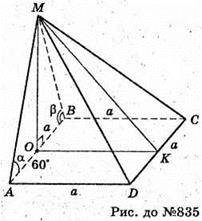
Нехай дано піраміду MABCD, в основі якої лежить квадрат,
AB = BC = CD = AD = а. Грань МАВ + ABCD, MO + AB, BK + AB, ∠MOK = 90°,
∠ MOK – лінійний кут двогранного кута при ребрі AB.
MO + ABCD, AO + AD, MA + AD, ∠MAO = α, ∠MAO – лінійний кут двогранного кута при ребрі AD. OB + BC, MB + BC, ∠MBO = β, ∠MBO – лінійний кут двогранного кута. Нехай AO = х, тоді OB = a – x.
ΔAMO: MO = x tg α. ΔМОВ. MO = (а – х) tg β;
X tg α + (а – x) tg β; x tg α = а tg β – x tg β;
X tg α + x tg β = a tg β; x(tg х + tg β) = a tg β;
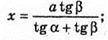MO = x tg α;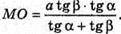 
Відповідь: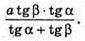 
836.
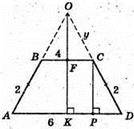
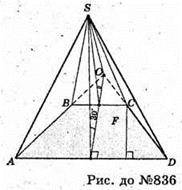
Нехай дано піраміду, в основі якої лежить трапеція ABCD, у якої
AB = CD = 2 см, BC = 4 см. AD = 6 см. Грань SAB + (ABCD),
Грань SCD + (ABCD), SO + (ABCD), SO – висота піраміди.
OK + AD, тоді за теоремою про три перпендикуляри SK + AD.
∠SKO = 30°, ∠SKO – лінійний кут двогранного кута при ребрі AD.
SO + (ABCD), (OFBC), SF + BC. ∠SFO – суміжний з лінійним кут двогранного кута при ребрі BC. ∠KFS – лінійний кут двогранного кута при ребрі BC.
CP + AD, CP – висота трапеції ABCD. PD = (6 – 4) : 2 = 1.
ΔCPD – прямокутний. CP2 = CD2 – PD2 = 4 – 1 = 3;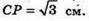 
ΔSOK – прямокутний. SO – висота піраміди.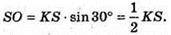 
ΔOBC – AOAD. BC? AD.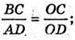 
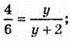
4у + 8 = 6у; 2у = 8; у = 4. OC = = 4; OD – OC + CD = 4 + 2 = 6 (см).
ΔOKD. OK2 = OD2- KD2;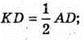 
OK2 = 36 – 9 = 27;
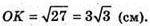
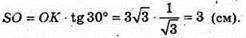
ΔSOF – прямокутний.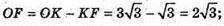 
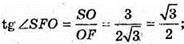
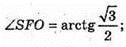
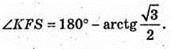
837.
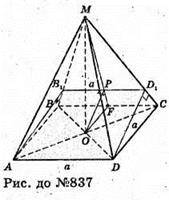
Див. рис.
838.
А)
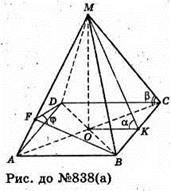
Нехай дано правильну піраміду, у якої ∠MCO = β – кут нахилу бічного ребра до площини основи. MO + ABCD; OK + DC; MK + DC.
∠MKO = α – кут нахилу бічної грані до площини основи.
γ = ∠AMB – плоский кут при вершині піраміди. DF + ВАМ; BF + AM.
∠DFB = φ – двогранний кут при бічному ребрі.
Нехай AD = а;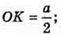 
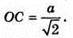
ΔMOC – прямокутний.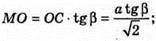 
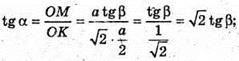
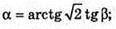
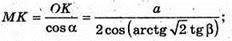
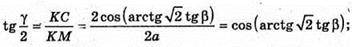
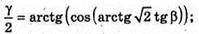
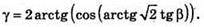
Б)
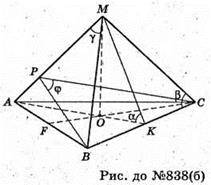
Нехай дано трикутну піраміду, ∠AMB = у – плоский кут при вершині піраміди.
∠OCM = β – кут нахилу бічного ребра до площини основи.
OK + BC, MK + BC. ∠MKO = α – кут нахилу бічної грані до площини основи.
BP + AM, CP + AM; φ = ∠BPC – кут при бічному ребрі.
AB = a; OE = r;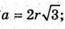 
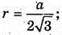
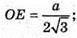
OC = R;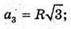 
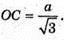
ΔOMC;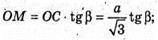 
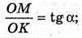
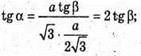A = arctg(2 tg β).
ΔОМК.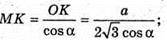 
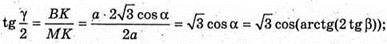
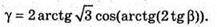
В)
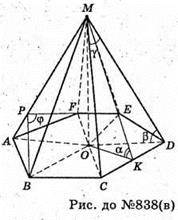
Нехай дано правильну шестикутну піраміду MABCDEF.
AB = BC = CD = ED = EF = AF = a. ∠MDO = β – кут нахилу бічного ребра MD до площини основи. OK + CD, MK + CD. ∠MKO – лінійний кут двогранного кута при ребрі CD. γ = ∠CMD — плоский кут при вершині піраміди.
BP + AM; FP + AM.
∠ BPF = φ – двогранний кут при бічному ребрі.
AB = а6 = R; OD =AB = a; OK = r,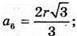 
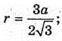
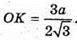
ΔMOD. MO = OD tg β = a tg β.
ΔΜΟΚ.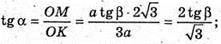 
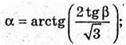
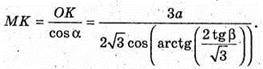
ΔМСК.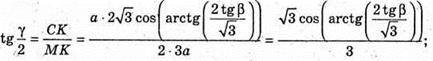 
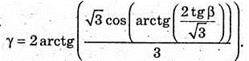
839.
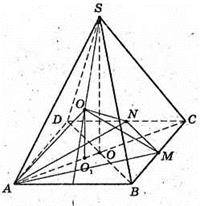
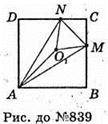
Нехай дано правильну чотирикутну піраміду SABCD, всі ребра якої дорівнюють a. AB – = BC = CD = AD = a. AS = BS = CS = DS = а. M? BC; N? DC; P? SAB.
PAMN – правильна трикутна піраміда.
ΔANM – правильний. P проектується в центр кола, описаного навколо правильного ΔANM – точку O1. O1M = O1N = O1A – радіуси описаного кола.
PA = PM = PN, точка P рівновіддалена від вершин основи ΔANM.
ΔABS = ΔBSC = ΔCDS – рівносторонні трикутники.
840.
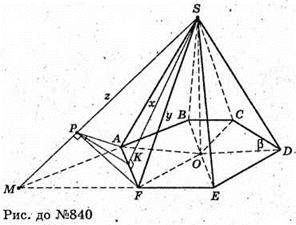
Нехай дано правильну шестикутну піраміду SABCDEF, сторона основи якої
AB = BC = CD = DE = EF = AF = a,
SK – апофема. FP + SM; AP + SM; SM – лінія перетину граней SAB і SEF,
∠FPA = α – кут між гранями SAB і SEF.
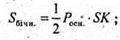Росн. = 6а.
Знайдемо SK. Нехай SK = х.
AFPA – рівнобедрений, PA = PF, PK + AF;
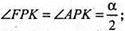
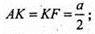
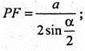
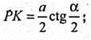
ΔSKF – прямокутний. SK = х, SF = у,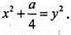 
ΔPSK – прямокутний. SP2 + PK2 = SK2;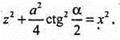 
ΔSPF – прямокутний. SP2+ PF2 =SF2;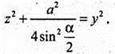 
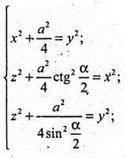
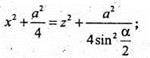
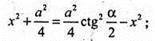
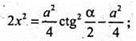
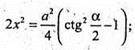
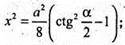
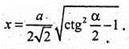
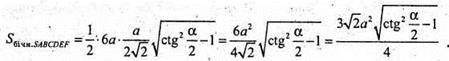
842.
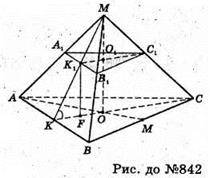
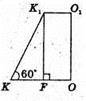
Нехай дано правильну трикутну зрізану піраміду, сторона нижньої основи m, двогранний кут при ребрі основи ∠K1KO = 60°, OK + AB, K1K + AB.
Площа повної поверхні дорівнює Q: Нехай сторона верхньої основи х.
A1B1 = B1C1 = A1C1 = х.
Проведемо K1F + КО; KO – радіус кола, вписаного в основу ΔABC.
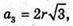
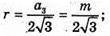
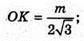
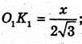
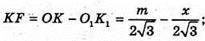
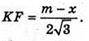
ΔK1KF – прямокутний.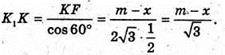 
Площа повної поверхні: 
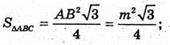
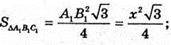
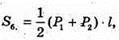де P1 = 3 m, P2= 3x; l = K1K.
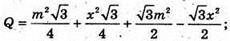
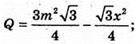
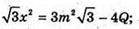
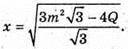
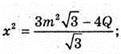
Відповідь: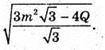 
843.
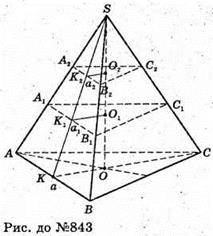
Нехай дано правильну трикутну піраміду.
Площа бічної поверхні дорівнює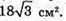 
Площа повної поверхні дорівнює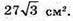
Площа основи – площа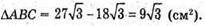 
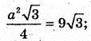
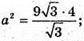а2 – 36, отже, сторона нижньої основи 6 см.
Висоту піраміди поділено на три частини. SO2 = O2O1 = O1O, через точки поділу проведено перерізи, паралельні основі.
Паралельні перерізи відтинають подібні піраміди.
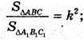
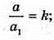
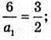a1 = 4 (см);
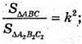
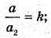
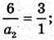а2 = 2 (см).
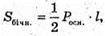де l = SK.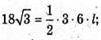 
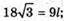
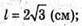
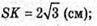
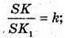
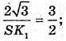
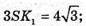
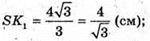
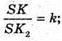
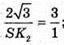
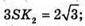
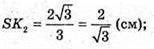
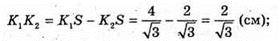
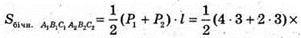
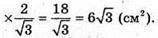
Відповідь: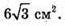 
844.
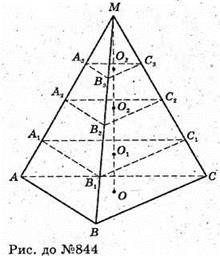
Нехай дано зрізану піраміду ABCA3B3C3. Площини перерізів, паралельних основам, ділять висоту зрізаної піраміди OO3на три рівні частини.
OO1= O1O2 = O2O3.
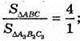
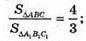
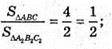
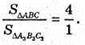
845.
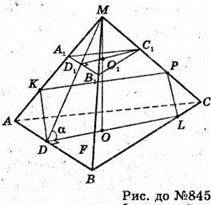
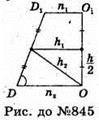
Нехай дано правильну трикутну зрізану піраміду, сторона AB = BC = AC = 3а;
A1B1 = B1C1 = A1C1 = 2а. MD + АB, OD + АВ, ∠MDO = α, кут між бічною гранню та площиною основи. Переріз зрізаної піраміди площиною, яка проходить через центр нижньої основи і середню лінію бічної грані.
KPLD – переріз. KP? AC; KP – середня лінія трапеції АА1С1С.
DL? AC, DL? PK.
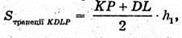де h1 – висота трапеції KDLP.
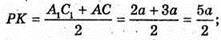
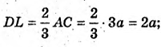
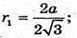
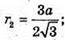
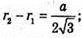
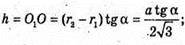
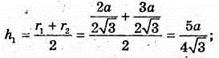
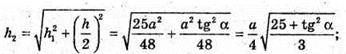
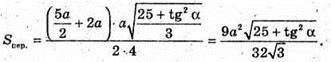
846.
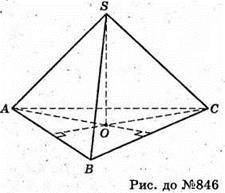
Нехай дано трикутну піраміду, в якій висота SO проходить через точку O – точку перетину висот основи ΔАВС.
AS, SC, SB – бічні ребра піраміди. AB, ВС, AC – ребра основи. AS і BC – мимобіжні ребра піраміди. AS2 + BC2 = SC2 + AB2 = SA2 + BC2.
847.
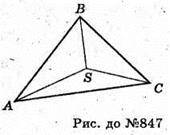
Нехай дано трикутну піраміду SABC, тригранний кут при вершині S прямий.
∠ASB = ∠CSB = ∠ASC = 90°.
Нехай AB = BC = AC = а.
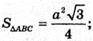
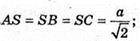
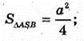
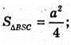
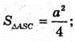
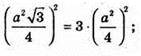
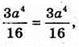що й треба було довести.
848.
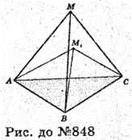
Нехай піраміда MABC і піраміда M1ABC мають спільну основу – ААВС,
Сума ребер внутрішньої піраміди може бути більшою за суму ребер зовнішньої піраміди.
849.
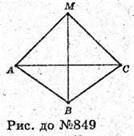
Нехай дано трикутну піраміду, у якої всі грані мають рівні площі.
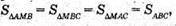Отже, всі грані – рівні трикутники.
(1 votes, average: 5.00 out of 5)
Loading...