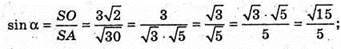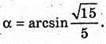Поділ відрізка в заданому відношенні
44.
А) М – середина PQ; Р( 1,2; -3; 6,3), Q(-2,6; 3,2; -5,1);
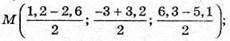М(-0,7; 0,1; 0,6);
Б)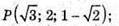
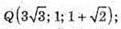
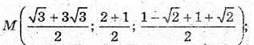
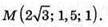
45.
А) К – середина АВ; М – середина CD.
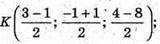
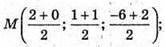
К(1; 0; -2); М( 1; 1; -2).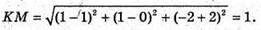 
Б) Р – середина АС; Z – середина BD.
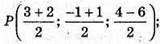
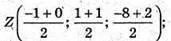
Р(2,5; 0; 1); Z(-0,5; 1; -3).
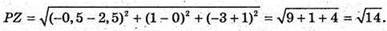
46.
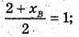2 + хв = 2; хв = 0;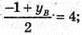 
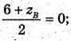6 + zв = 0; zв = -6. Отже, B(0; 9; -6).
47.
М(1; -1; 2), N(-3; 2; 4).
М – середина AN;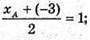 
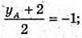
УA = -4;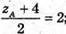 
zA = 0; Отже, 4(5; -4; 0).
N – середина MB;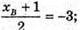 
хв = -7;
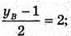Ув= 5; 
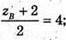zв = 6. Отже, В(-7; 5; 6).
48.
АK – медіана ΔАВС, тоді K – середина ВС.
К(0; -1; 0);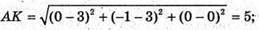 
ВР – медіана ΔАВС, тоді Р – середина АС
Р(4; 0; -1);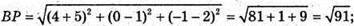 
CD – медіана ΔАВС, тоді D – середина АВ.
D(-1; 2; 1);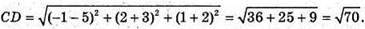 
49.
N – середина EF; М(-2; 3; 0); Р – середина FK; Р(-1; 0; -2);
С – середина EK; С(0; 1; 0).
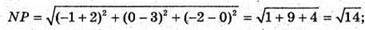
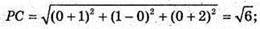
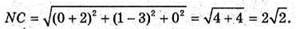
50.
Μ – середина AB: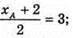
XA = 4; 
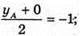yA = -2;
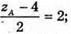zA = 8. Отже, Α(4; -2; 8).
N – середина ВС: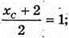 
хC = 0;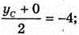
YC = -8;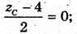 
zC = 4. Отже, C(0; -8; 4).
51 .
Якщо AM – медіана, то М – середина ВС,
Тоді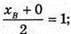 
хв = 2; 
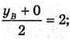yв = 4;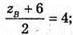 
Zв = 2. Отже, В(2; 4; 2)
BN – медіана, тоді N – середина АС, N( 1; -2; 4).
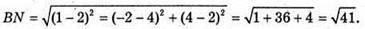
52.
А)А(1г-3; 12); В(0;.2; 6); С(3; 3; -.10); D(4; -2; -4).
Знайдемо О – середину АС: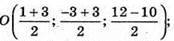 
O(2; 0; 1).
Знайдемо О1 – середину BD. O1(2; 0; 1). О і О1 збігаються.
Отже, діагоналі перетинаються і точкою перетину діляться навпіл.
Тому ABCD – паралелограм,
Б) А(4; 2; -5); В(-6; 2; 8); С( 2; -3; 9); D(12; 2; 4).
Знайдемо середину АС: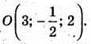 
Знайдемо середину BD: O1(3; 2; 2).
Середини діагоналей чотирикутника не збігаються.
Отже, у чотирикутнику ABCD не виконується умова:
Діагоналі паралелограма точкою перетину діляться навпіл.
Тому ABCD не є паралелограмом.
53.
А) Знайдемо О – середину АС: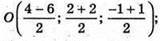
O(-1; 2; 0).
Точка О є серединою і діагоналі BD.
Тому: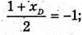 
хD = 8; 
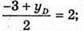yD = 7; 
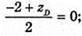zD = 2.
Отже, D(-3; 7; 2).
Б) О – середина АС і BD. O(4; 2; -2).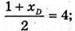 
1 + хD = 8; xD = 7;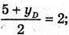 
5 + yD = 4; уD = -1;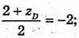 
2 + zD = -4; zD = -6. Отже, D(7; -1; -6).
54.
О – середина АС, тому
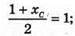xC = 4;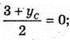 
УC = -3;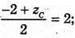 
zC = 6.Отже, C(1; -3; 6).
О – середина BD.
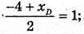-4 + xD = 2; xD = 6;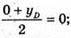 
YD = 0;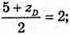 
5 + zD = 4; zD = -1. Отже, D(6; 0; -1).
55.
A) AM : MB = 2, тобто AM : MB = 2 : 1. A(-5; 4; 2), B(1; 1; -1).
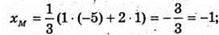
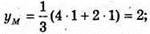
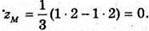
Отже, M(-1; 2; 0).
Б) A(1; -1; 2), B(2; -4; 1), λ = 0,5, AM : MB = 1 : 2
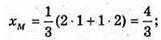
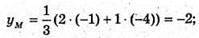
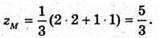
Отже,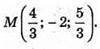 
В) A(1; 0; -2), B(9; -3; 6),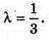 
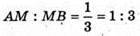
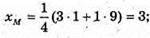
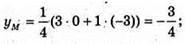
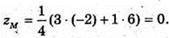
Отже,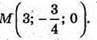 
56.
ΔMNP: A(3; 2; 4), N(1; 3; 2), P(-3; 4; 3).
Медіани трикутника перетинаються в точці, яка ділить їх у відношенні 2:1,
Починаючи від вершини. MZ – медіана, Z – середина NP.
Z(-1; 3,5; 2,5). Знайдемо координати точки О, яка ділить MZ у відношенні 2 : 1.
MO : OZ = 2 : 1.
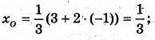
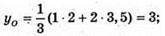
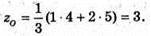
Отже,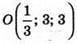 
– точка перетину медіан ΔMNP.
57.
А) Якщо Р лежить на осі z, то Р(0; 0; z), О – середина MN, М(а; -2; 3), N(2; 6; -1),
Тоді: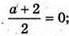 
а = -2; 
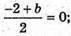б = 2.
Б) М(2а2; – b; 1), N(а – 1; 1; 5).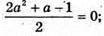
2а2 + о – 1 = 0; а = -1 або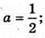
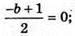b = 1.
В) М(3а; 6 + 1; 4), N(b; 1-а; -2).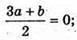
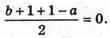
Маємо систему:
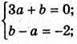
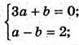
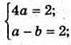
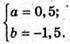
58.
ΔАBС: А(1; -1; 2), B(4; 2; -1), С(1; 5; 2)
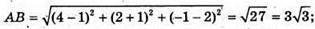
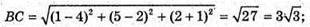
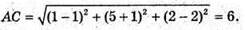
ΔABC – рівнобедрений, АС – основа і найбільша сторона.
Тому висота, проведена до найбільшої сторони – це висота з вершини В.
ВК + АС, K – середина АС (оскільки ΔABC – рівнобедрений).
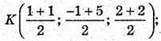К(1; 2; 2).
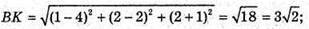
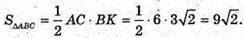
59.
А(1; 3; -1), В(3; -1; 1), С(3; 1; -1).
А)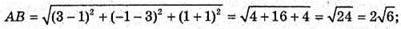 
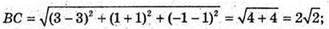
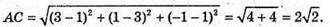
АС – найбільша сторона ΔABC – рівнобедрений.
СK – висота, проведена до найбільшої сторони, і медіана.
K – середина АВ; К(2; 1; 0).
Б)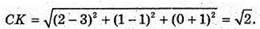 
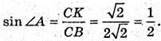
Звідси ∠A = 30°, ∠B = ∠А = 30°,
∠C = 180° – (30° + 30°) = 120°.
В)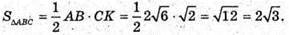 
60.
A1(1; -2; 3), А2(З; 2; 1), А3(-1; 4; 1).
1-й випадок. А1А2 – діагональ, О – середина Α1Α2. O(2; 0; 2),
О – середина А3A4.
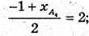-1 + хА4 = 4; хА4 = 5; 
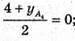4 + уА4 = 0; уА4 = -4;
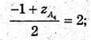-1 + z А4 = 4; z А4 = 4.
Отже, А4(5; -4; 4).
2-й випадок. А1А3 – діагональ. О – середина А1А3, O(0; 1; 1).
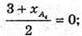3 + xА4 = 0; х А4 = -3; 
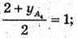2 + уА4 = 2; у А4= 0;
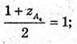1 + z А4 = 2; г А4 =1. Отже, А4(-3; 0; 1).
3-й випадок. А 2А3 – діагональ. О – середина А 2А3 O(1; 3; 0).
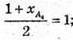1 + х А4 = 2; x А4 =1; 
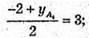-2 + уА4 = 6; уа4 = 8;
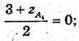3 + z А4 = 0; z А4= – 3.
Отже, А4(1; 8; -3).
Задача має три розв’язки.
61.
АK – медіана, K – середина ВС.
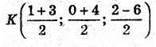або K(2; 2; -2).
О 1 – точка перетину медіан ділить АK у відношенні 2:1,
Тобто AO1 : О1K = 2 : 1.
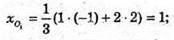
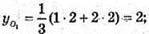
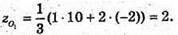
O1(1; 2; 2), O(0; 0; 0) – початок координат.
62.
А)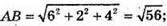 
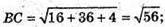
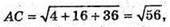
ΔABC – рівносторонній, тому О – центр описаного кола –
Знаходиться в точці перетину медіан; АР – медіана. Р(3; 2; 0).
АО : ОР = 2 : 1;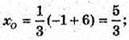 
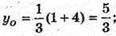
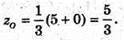
Отже,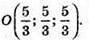 
Б) АВ2 – 9 + 1 + 0 = 10; ВС2 = 1 + 9+ 4 – 14; АС2 = 16 + 4 + 4 = 24.
Нескладно замітити, що АС2 = АВ2 + ВС2, тому ΔАВС – прямокутний,
О – центр описаного кола. О – середина АВ,
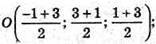O(1; 2; 2).
63.
А)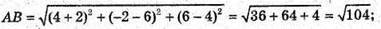 
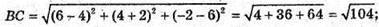
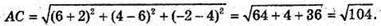
ΔАВС – рівносторонній. Центром кола, вписаного в цей трикутник,
Є точка перетину медіан (в рівносторонньому трикутнику медіани є бісектрисами).
АK – медіана, K (5; 1; 2). О – центр вписаного кола. AO : ОK = 2 : 1.
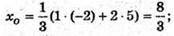
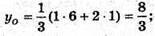
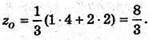
Отже,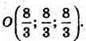 
Б)
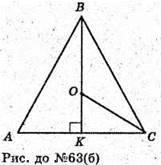
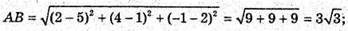
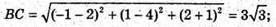
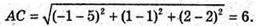
ΔАВС – рівнобедрений. АС – основа. О – центр кола, вписаного в ΔАВС,
Лежить на ВК – бісектрисі ΔАВС, оскільки АВ = ВС, то ВK – бісектриса і медіана.
К – середина АС, K(2; 1; 2), О лежить також на бісектрисі ∠C ΔАВС.
За властивістю бісектриси трикутника, бісектриса СК ділить ВK точкою О
У відношенні ВО : ОК = ВС : СK.
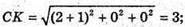
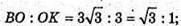
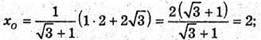
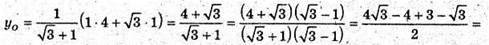
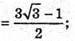
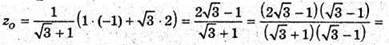
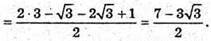
Отже,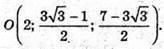 
64.
ABCD – основа куба, квадрат.
АС – діагональ.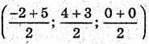 
або 
–
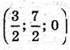Точка перетину діагоналей основи куба.
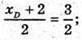xD = 1; 
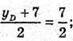yD = 0; 
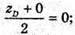zD = 0;
Отже, O(1; 0; 0).
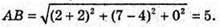
Оскільки довжина сторони куба дорівнює 5, то А1(-2; 4; 5), B1(2; 7; 5), C1(5; 3; 5),
D1( 1; 0; 5) або А 1 (-2; 4; -5), В1(2; 7; -5), С1(5; 3; -5), D(1; 0; -5).
Тоді координати точок перетину діагоналей є серединою діагоналі АС1, тобто
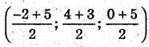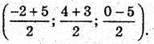
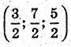або 
або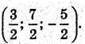 
65.
СК – медіана, K – середина АВ.
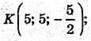точка М ділить СK у відношенні CM : МK – 2 : 1, тоді
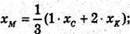
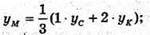
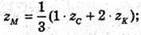
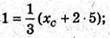
ХC + 10 = 3;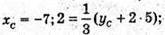 
уC + 10 = 6; уC = -4;
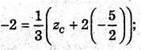ZC – 5 = -6; zС = -1.
Отже, С(-7; -4; -1).
66.
BL – бісектриса ΔАВС, тому AL : LC = АВ : ВС.
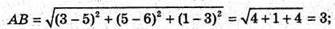
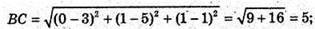
А(5; 6; 3), С(0; 1; 1), AL : LC = 3 : 5.
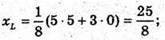
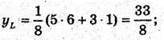
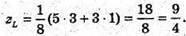
Отже,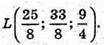 
67.
ML – бісектриса, L ділить сторону NK у відношенні NL : LK = MN : МК.
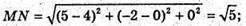
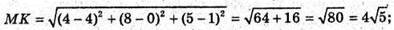
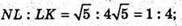
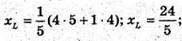
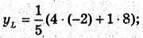
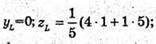
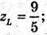
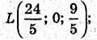
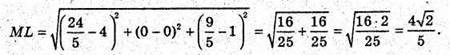
68.
ΔАВС – рівносторонній, О1 – точка перетину медіан, О – початок координат, OO1 – шукана відстань. Знайдемо координати О1. АК – медіана ΔАВС, K – середина ВС, K(0; 3; 3). ΑO1 : О1K = 2 : 1.
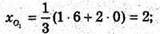
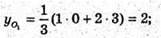
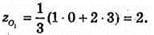
Отже, O1(2; 2; 2).
Тоді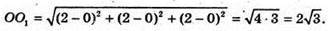
69.
Пряма АВ площини о. лежить в площині ху,
Пряма KР площини β лежить в площині ху.
АВ є середня лінія ΔОKР (О – початок координат).
Тому АВ? KР. Аналогічно ВС? РТ.
Прямі AS і ВС перетинаються і лежать у площині α.
Прямі KР і РТ перетинаються і лежать у площині β.
АВ? KР, ВС? РТ, тому α ? β.
Відстань між а і β дорівнює відстані між точками перетину медіан ΔABC і ΔKРТ.
О1 – точка перетину медіан ΔАВС, АK – медіана, K – середина ВС, K(0; 1; 1).
АО1 : Ο1Κ = 2 : 1.
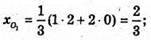
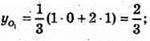
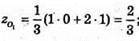
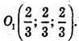
О2 – точка перетину медіан ΔАKРТ, KS – медіана; S – середина РТ, S(0; 2; 2).
KO2 : O2S = 2 : 1.
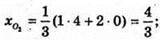
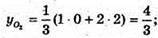
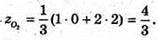
Отже,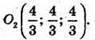 
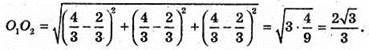
70.
А)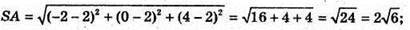 
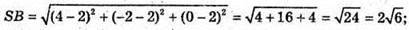
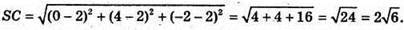
Бічні ребра рівні, тому О – центр кола, описаного навколо ΔАВС,
Де SO – висота піраміди.
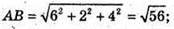
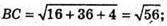
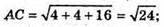
ΔАВС – рівнобедрений.
ВK – медіана;K – середина АС; К(-1; 2; 1).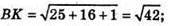 
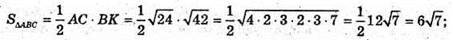
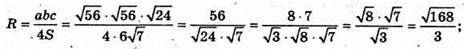
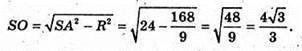
α – кут нахилу ребер до площини основи.
З ΔSOA – прямокутного: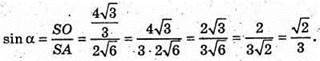 
Б)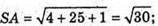 
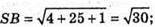
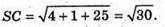
Бічні ребра рівні, тому О – центр кола, описаного навколо ΔABC;
SO – висота піраміди.
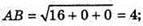
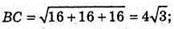
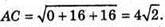
ΔABC – рівносторонній. За формулою Герона знайдемо S.
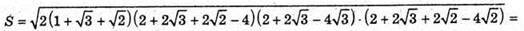
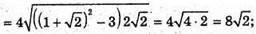
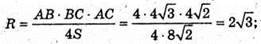
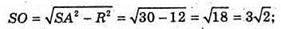α – шуканий кут.
(1 votes, average: 5.00 out of 5)
Loading...