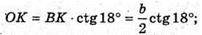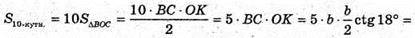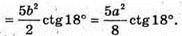Правильні многогранники
862.
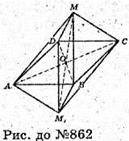
Якщо у піраміді всі ребра рівні, то з них можна скласти правильний октаедр.
АB = а;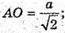 
AM = а;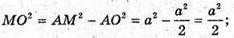 
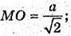
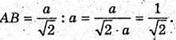
Відповідь: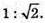 
863.
А) так; б) так.
864.
А) ні; б) так; в) ні.
865.
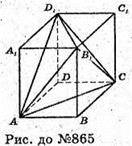
Якщо з однієї вершини куба провести три діагоналі бічних граней і їх кінці з’єднати відрізками, то утворена піраміда буде тетраедром.
866.
Сума плоских кутів при вершині правильних многогранників:
1)
2) тетраедр 3 × 60° = 180°;
3) октаедр 4 × 60° = 240°;
4) ікосаедр 5 × 60° = 300°;
5) додекаедр 3 × 108° = 324°.
868.
Із центра куба його ребро видно під кутом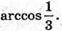 
Із центра правильного октаедра його ребро видно під кутом 90°.
869.
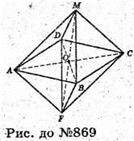
Нехай дано правильний октаедр. FO = AO = OC = OM = 1 дм.
DAOM – прямокутний. AM2 = AO2 + OM2= 1 + 1 = 2;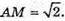 
Відповідь: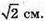 
870.
Ребро октаедра AM = AB = 4 см.
Переріз ABCD – площина симетрії цього октаедра. ABCD – квадрат.
SABCD = 42 = 16 (см2). Переріз
MDFB – ромб.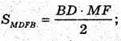 
BD – діагональ квадрата ABCD.
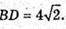
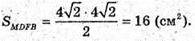
871.
Нехай ребро ікосаедра дорівнює а. Площа поверхні ікосаедра:
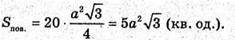
872.
Площа поверхні правильного октаедра дорівнює S.
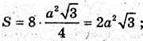
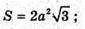
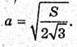
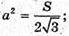
873.
Якщо ребро правильного ікосаедра збільшити у 3 рази, то площа поверхні ікосаедра збільшиться. а – ребро;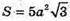 
– площа;
За – нове ребро;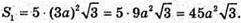 
Площа збільшиться у 9 разів.
874.
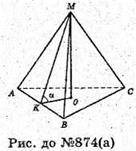
А) нехай дано тетраедр. MO + ABC, OK + AB, MK + AB.
PMKO = а – лінійний кут двогранного кута при ребрі основи.
MB = a; AB = a. DMKB – прямокутний.
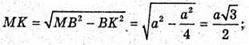
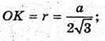
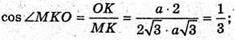
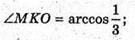
Б)
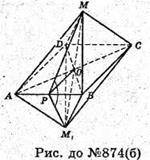
MO + ABCD; OP + АВ; MP + AB; M1P + AB; DMPM1- лінійний кут
Двогранного кута при ребрі АВ. AB = a; MB = а;
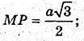
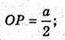
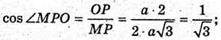
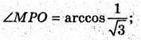
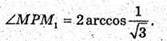
878.
Вершини куба будуть вершинами правильного тетраедра.
879.
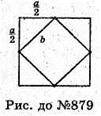
Нехай дано куб з ребром а.
Центри його граней є вершинами многогранника – октаедра.
B – ребро октаедра.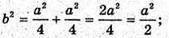 
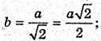
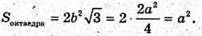
880.
Ребро правильного тетраедра дорівнює а.
Многогранник, вершинами якого є центри граней даного тетраедра,
Буде тетраедр з ребром b.
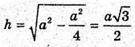– висота грані тетраедра.
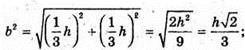
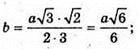
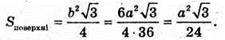
881.
Ребро правильного октаедра дорівнює а.
Центри граней даного октаедра є вершинами куба.
D2 = а2 + a2; d2= 2а2: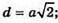 
b – ребро куба.
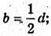
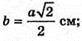
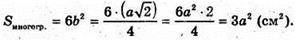
882.
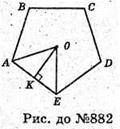
Нехай дано правильний додекаедр з ребром m.
Грані додекаедра – правильні п’ятикутники.
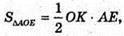
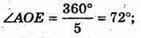де AE = m;
PAOK = 36°;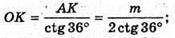 
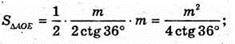
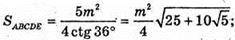
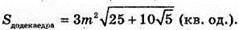
Відповідь: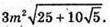 
883.
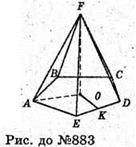
AF, FE, FD, FC, FB – ребра грані ікосаедра.
DBEC – рівносторонній. FK + BC. OK + BC;
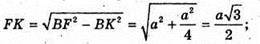
OK – радіус кола, вписаного в п’ятикутник ABCDE.
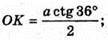
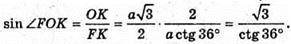
Кут при ребрі ікосаедра дорівнює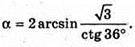 
884.
У правильному октаедрі протилежні ребра паралельні, тому що переріз октаедра є квадрат, протилежні грані лежать у паралельних площинах.
887.
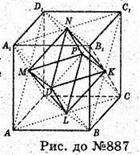
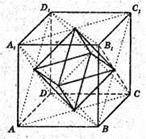
Перерізом тетраедрів AB1CD1і C1BA1D є правильний октаедр MNPKLD.
Він має 6 вершин, які знаходяться у точках перетину діагоналей грані куба, перерізом тетраедра є квадрат MPKD.
888.
Правильного многогранника, гранями якого є правильні n-кутники (при n і 6),
Не існує.
У всіх многогранних кутах сума плоских кутів при вершині менша 360°.
Плоский кут правильного n-кутника, якщо n = 6, 120°, 120°. 6 = 720°.
890.
У будь-якому многогранному куті сума плоских кутів при вершині менша ніж 360°. В тетраедрі у кожній вершині сходиться три ребра.
Плоский кут 3 × 60° = 180°. У октаедра 4 × 60° = 240°; у куба 3 × 90° = 270°; у додекаедра 108° × 3 = 324°; у ікосаедра 60° × 5 = 300°. Правильні многокутники з числом сторін більше або дорівнює шести не можуть бути гранями правильних многогранників, тому їх існує тільки п’ять.
893.
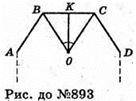
Нехай перерізом правильного ікосаедра є правильний десятикутник, тоді він проходить через середини його ребер. b – ребро десятикутника.
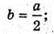
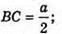PBOC = 360° : 10 = 36°;
(1 votes, average: 5.00 out of 5)
Loading...