Головна ⇒ 📌Довідник з математики ⇒ Приклади розв’язування системи тригонометричних рівнянь
Приклади розв’язування системи тригонометричних рівнянь
Математика – Алгебра
Тригонометричні функції
Приклади розв’язування системи тригонометричних рівнянь
1) 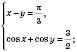
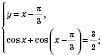
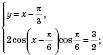
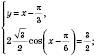
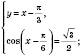
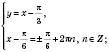
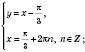
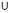
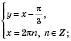
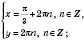
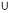
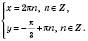
Відповідь: 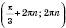 , n Є Z;
, n Є Z;
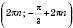 , n Є Z.
, n Є Z.
2) 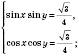
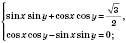
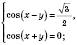
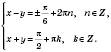
а) 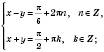
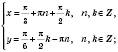
б) 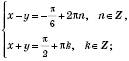
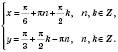
Відповідь:
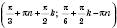 , n, k Є Z;
, n, k Є Z;
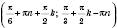 , n, k Є Z.
, n, k Є Z.
Related posts:
- Розв’язування систем тригонометричних рівнянь УРОК 27 Тема. Розв’язування систем тригонометричних рівнянь Мета уроку: познайомити учнів з окремими прийомами розв’язування систем тригонометричних рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування домашніх завдань: вправа № 2 (10; 18; 26; 38). 2. Усне розв’язування тригонометричних рівнянь, використовуючи таблицю “Тригонометричні рівняння”. 1 2 3 4 1 Sin x = 0 Cos […]...
- Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій при зростанні “a” від 0 до 2п Зміну , , , при зростанні від 0 до описано в табл. 2. Позначення: – зростає; – спадає....
- Розв’язування тригонометричних рівнянь, систем та нерівностей УРОК 31 Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування нерівностей із домашнього завдання. 2. Колективне розв’язування нерівностей: A) sin 2x sin x – cos 2x cos х . Sin 2x sin x – cos 2x […]...
- Розв’язування найпростіших тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних рівнянь 1. cos x = a Розв’язки рівняння шукатимемо, спираючись на рисунок 1 або на рисунок 2. Якщо , розв’язків немає. , , . , , . , , . Рис. 2 Загальний випадок : , x = ±arccosa + 2πn,. У випадках, коли , , теж […]...
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Деякі способи розв’язування тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Деякі способи розв’язування тригонометричних рівнянь 1. Рівняння, що зводяться до квадратних . легко виразити через за допомогою основної тригонометричної тотожності : . Отже, ; . Нехай , . ; ; . 1) ; , k Є Z. 2) ; , k Є Z. Відповідь: , k Є Z; , k […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Розв’язування найпростіших тригонометричних нерівностей Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних нерівностей Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола. Приклади 1) . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму . Вона перетинає коло у двох точках. Одна з них відповідає куту або , друга – куту або . Ці дві точки розбивають коло на […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Розв’язування тригонометричних рівнянь способом розкладання на множники УРОК 24 Тема. Розв’язування тригонометричних рівнянь способом розкладання на множники Мета уроку: фрмування умінь учнів розв’язувати тригонометричні рівняння способом розкладання на множники. І. Перевірка домашнього завдання Перший учень пояснює розв’язування вправи № 2 (23), другий учень – вправи № 2 (30), третій – вправи № 2 (37). II. Сприймання і усвідомлення нового матеріалу Багато тригонометричних […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...
- Розв’язування однорідних тригонометричних рівнянь УРОК 25 Тема. Розв’язування однорідних тригонометричних рівнянь Мета уроку: формування умінь учнів розв’язувати однорідні тригонометричні рівняння. І. Перевірка домашнього завдання 1. Обговорення розв’язування вправи № 2 (6; 9; 11) за готовими розв’язаннями. 2. Розв’язування аналогічних вправ. А) 1 + cos x + cos 2x = 0; Б) cos4 x – sin4 x = ; В) […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...
- Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину. Приклад. Розв’яжіть рівняння . Побудуємо графіки функції і в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину. […]...
- Розв’язування показникових рівнянь і систем УРОК 47 Тема. Розв’язування показникових рівнянь і систем Мета уроку. Формування умінь учнів розв’язувати показникові рівняння і системи різними способами. І. Перевірка домашнього завдання. Три учні відтворюють на відкидних дошках розв’язування вправ: 1 учень – № 34 із “Запитань для повторення”; 2 учень – № 1 (12-14); 3 учень – № 1 (15, 16). У […]...
- Розв’язування рівнянь Математика – Алгебра Раціональні числа Розв’язування рівнянь Властивості рівнянь Корені рівнянь не змінюються, якщо до обох частин додати будь-який доданок. Отже, при розв’язуванні рівнянь доданки можна переносити з однієї частини в другу, змінюючи при цьому їхні знаки на протилежні. Корені рівнянь не змінюються, якщо обидві його частини помножити або поділити на одне й те ж […]...
- Розв’язування задач за допомогою рівнянь – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Розв’язування задач за допомогою рівнянь Для розв’язування таких задач зручно користуватися таблицями. Задача 1. В одній шафі було в 6 разів більше книг, ніж у другій. Після того як із однієї шафи взяли 46 книг, а з другої – 18 книг, у першій шафі залишилося на 97 книг […]...
- Системи рівнянь з двома змінними УРОК 64 Тема. Системи рівнянь з двома змінними Тестові завдання 1. Яка з пар чисел є розв’язком рівняння 3х2 – 2ху +1 = 0 ? А) (1; 2); б) (2; 2); в) (0; 3); г) (0;0)? 2. Яка з пар чисел є розв’язком системи А) (3; 0); б) (2; 1); в) (1; 2); г) (0; […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- Розв’язування показникових рівнянь і систем показникових рівнянь УРОК 48 Тема. Розв’язування показникових рівнянь і систем показникових рівнянь Мета уроку. Формування уміння розв’язувати показникові рівняння і системи показникових рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування вправи № 1 (25, 28, 30, 46). 2. Усне розв’язування показникових рівнянь за допомогою таблиці 20 для усних обчислень “Показникові рівняння” 1 2 3 4 […]...
- Системи лінійних рівнянь із двома змінними Урок № 82 Тема. Системи лінійних рівнянь із двома змінними Мета: перевірити рівень опанування учнями навчального матеріалу та вироблених умінь і навичок з теми, передбачених програмою з математики. Тип уроку: контроль засвоєння знань, умінь, навичок. Хід уроку І. Організаційний момент 1. Перевірка готовності до уроку. 2. Зібрати зошити з домашньою контрольною роботою. II. Умова тематичної […]...
« БАТИК
ЛІГВО »