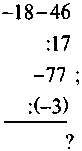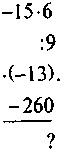Розв’язування лінійних рівнянь з однією змінною
Урок № 99
Тема. Розв’язування лінійних рівнянь з однією змінною
Мета: закріпити знання учнів про властивості рівносильності рівнянь та способи їх застосування для розв’язування лінійних рівнянь з однією змінною; вдосконалити вміння учнів розв’язувати лінійні рівняння з однією змінною з використанням зазначених вище знань.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
Кілька учнів біля дошки розв’язують вправи домашнього завдання (найцікавіші
Усні вправи
1. Обчисліть:
А) |
| Б) |
|
2. Знайдіть таке число, яке кожне з наступних рівнянь перетворить у правильну числову рівність:
А) 7х – 3 = 3х + 17; б) 3(3х – 5) = 8х – 10; в) 8х – 6х = 10.
3. Використовуючи правильну рівність 5-2-3 = 2-3+1, складіть рівняння, корінь якого дорівнює: а) 2; б) -3.
4. * За якої умови правильною нерівність (рівність)?
А) а < – а; б) – а < а; в) – а > а; г) – а = а.
III. Відпрацювання знань
Під час перевірки домашнього завдання
– означення кореня рівняння (з однією змінною);
– властивості (рівносильності) рівнянь;
– схему розв’язування (лінійних) рівнянь з однією змінною;
– деякі властивості раціональних чисел (протилежні числа).
IV. Вдосконалення вмінь
@ Хоча основна дидактична мета уроку – вдосконалення вмінь і навичок розв’язувати лінійні рівняння з однією зміною, автор вважає доречним показати учням, що певна група рівнянь, що не є лінійними, може бути зведена до лінійних за певних умов.
Тому, окрім традиційних лінійних рівнянь високого рівня складності, можна запропонувати для розв’язування інші види рівнянь (пропорції з невідомими членами, а також простіші рівняння з параметрами).
1. Розв’яжіть рівняння:
А) 0,5 + 2х = 1,5 + 3х;
Б) 7 – 2(х – 4,5) = 6 – 4х;
В) 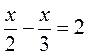 ;
;
Г) 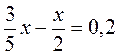 ;
;
Д) 11х + 5 = 5х – 12 – 4 – х;
Є) 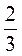 (х + 3) =
(х + 3) = 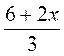 ;
;
Ж) 0,2(х – 1) + 0,5(3х – 9) = 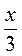 – 2;
– 2;
З) 5 – 3(х – 2(х – 2(х – 2))) = 2;
К) (13,4 – у) – 4,3 – 20,05 = 78,05 + 6,7у.
2. Розв’яжіть рівняння, використовуючи основну властивість пропорції:
А) 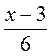 =
=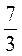 ; б)
; б) 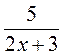 =
=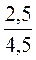 ; в)
; в) 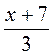 =
=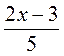 ; г)
; г) 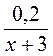 =
=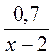 .
.
3. При яких значеннях (параметра) а:
А) рівняння ах – 4 = 3х має корінь, що дорівнює 8;
Б) 6(ах – 1) – а = 2(а + х) – 7 має корінь -1?
V. Підсумки уроку
Тестові завдання
1. Корінь рівняння 5х – 60 – х = 2х: 1) 10; 2) 15; 3) 30; 4) 5.
2. В якому випадку під час перенесення доданків з лівої частини в праву припустилися помилки?
A) 5 – х = 25 – 6х; 6х – х = 25 – 5;
Б) 3 + 6х = 9 – 3х; 6х + 3х = 9 + 3;
В) 2х – 1 = 1 – 4х; 2х + 4х = 1 + 1;
Г) -3х – 10 = 5х – х; -3х – 5х – х = 10.
3. Укажіть суму коренів рівнянь 5(10 – 4х) = 50 та -3(2 – х) = -9: 1) 2,5; 2) 0; 3) -1; 4) 5.
4. Корінь якого з наведених рівнянь дорівнює 0?
1) 3х – 6 = 6 – 3х;
2) 6 + 3х = 3х – 6;
3) 6х + 3 = 3 – 6х;
4) 3 – 6х = -3 – 6х.
VI. Домашнє завдання
1. Розв’яжіть рівняння: а) 4(3 – 2х) + 24 = 2(3 + 2х);
б) 0,2 (5у – 2) – 0,3(2у – 1) – 0,9;
В) 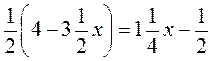 ;
;
Г) 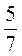 (0,21 – 1,4х) – 1 =
(0,21 – 1,4х) – 1 = 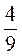 (0,36 – 4,5х).
(0,36 – 4,5х).
2. Розв’яжіть рівняння та виконайте перевірку: 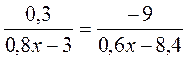 .
.
3. Оксана витратила и магазині 4,8 гри. Скільки грошей витратила Оля, якщо відомо, то Оксана витратила:
А) на 0,3 гри більше за Олю;
Б) на 0,5 гри менше від Олі;
В) в 2 раз більше за Олю;
Г) в 1,5 раза менше від Олі;
Д) 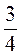 того, що витратила Оля;
того, що витратила Оля;
Є) 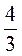 того, що витратила Оля;
того, що витратила Оля;
Ж) 25 % того, що витратила Оля;
З) на 35 % більше того, що витратила Оля?