Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a
УРОК 20
Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a
Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a.
Обладнання: Таблиця “Рівняння cos t = a”.
І. Перевірка домашнього завдання
Математичний диктант
Обчисліть:
1) arcsin 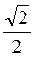 ; 2) arcos
; 2) arcos  ; 3) arctg
; 3) arctg  ; 4) arcsin
; 4) arcsin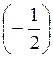 ; 5) arccos
; 5) arccos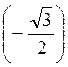 ; 6) arctg (-1);
; 6) arctg (-1);
7) arcctg (-1); 8) cos (arсcos 1); 9) sin 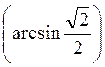 ; 10) arcsin
; 10) arcsin 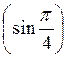
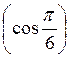 ; 12) arccos
; 12) arccos 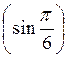 .
.Відповіді:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) –
; 4) – ; 5)
; 5) 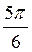 ; 6) –
; 6) – ; 7)
; 7) 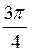 ; 8) 1; 9)
; 8) 1; 9) 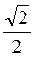 ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  .
.
II. Мотивація навчання та повідомлення теми уроку
Усім відомо, що квадратні рівняння можна розв’язувати за допомогою формули їх коренів, що значно спрощує роботу.
У математиці розглядають рівняння, у яких невідоме
Отже, наше завдання – вивести формули для розв’язування найпростіших тригонометричних рівнянь і навчитися розв’язувати тригонометричні рівняння, які приводяться до найпростіших.
На сьогоднішньому уроці розглянемо розв’язування рівняння cos t = a.
ІІІ. Сприймання і усвідомлення матеріалу про розв’язування рівняння cos t = а
Демонструється таблиця 8.
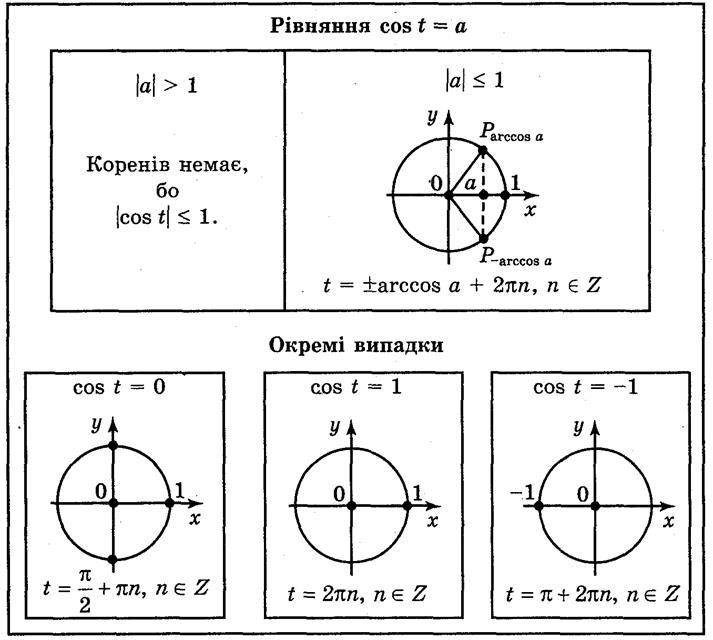
Пояснення вчителя
1. Якщо |а| > 1, то рівняння cos t = а не має розв’язків, по-скільки |cos t| < 1 для будь-якого t.
2. Якщо |а| < 1, то враховуючи те, що cos t – абсциса точки Рt одиничного кола, маємо: абсцису, рівну а, мають дві точки (рис. 122) одиничного кола(на осі ОХ відкладемо число а і через побудовану точку проведемо пряму, перпендикулярну до осі абсцис, яка перетне коло у двох точках 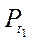 і
і  . Тоді
. Тоді
T1 = arccos a + 2?n, n Z,
Z,
T2 = – arccos а + 2?n, n Z.
Z.
T = ± arccos a + 2?n, n Z (1)
Z (1)
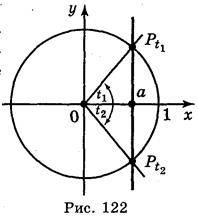
3. Якщо а = 1, то, враховуючи те, що cos t – це абсциса точки Рt одиничного кола, маємо: абсцису, рівну 1, має точка Рt утворена із точки Р0(1; 0) поворотом на кути 2?n, n Z. Отже, t = 0 + 2?n = 2?n, n
Z. Отже, t = 0 + 2?n = 2?n, n Z.
Z.
4. Якщо а = -1, то маємо t = n + 2?n, n Z. Корені рівнянь: cos t = 1, cos t = -1, cos t = 0 також можна одержати із формули t = ± arccos a + 2?n, n
Z. Корені рівнянь: cos t = 1, cos t = -1, cos t = 0 також можна одержати із формули t = ± arccos a + 2?n, n Z. Розглянемо приклади.
Z. Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння cos x = 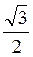 .
.
Згідно з формулою (1) маємо:
Х = ± arccos 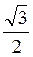 + 2?n, n
+ 2?n, n Z.
Z.
Оскільки arccos 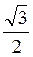 =
=  , то маємо: х = ±
, то маємо: х = ±  + 2?n, nєZ.
+ 2?n, nєZ.
Відповідь: ±  + 2?n, n
+ 2?n, n Z.
Z.
Приклад 2. Розв’яжіть рівняння cos x =  .
.
Оскільки  > 1, то рівняння коренів не має.
> 1, то рівняння коренів не має.
Відповідь: коренів немає.
Приклад 3. Розв’яжіть рівняння cos x = 0,37.
Згідно з формулою (1) маємо:
Х = arccos 0,37 + 2?n, n Z.
Z.
Значення arccos 0,37 знайдемо за допомогою мікрокалькулятора: arccos 0,37 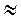 1,19, тоді х
1,19, тоді х 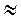 ± 1,19 + 2?n, n
± 1,19 + 2?n, n Z.
Z.
Відповідь: arccos 0,37 + 2?n 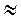 ± 1,19 + 2?n, n
± 1,19 + 2?n, n Z.
Z.
Приклад 4. Розв’яжіть рівняння cos x = –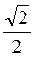 .
.
Згідно з формулою (1) маємо: х = ±arccos 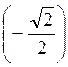 + 2?n, n
+ 2?n, n Z.
Z.
Оскільки arccos 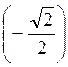 = n – arccos
= n – arccos 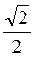 = n –
= n –  =
= 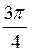 , то x = ±
, то x = ± 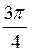 + 2?n, n
+ 2?n, n Z.
Z.
Відповідь: ± 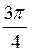 + 2?n, n
+ 2?n, n Z.
Z.
IV. Осмислення вивченого матеріалу
Виконання вправ______________________________
Розв’яжіть рівняння.
1. a) -2cos х = 1; б) cos 2х – 1 = 0; в) 2cos 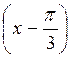 =
=  ; г)
; г)  – 2cos
– 2cos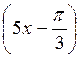 = 0.
= 0.
Відповідь: а)±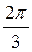 +2?n, n
+2?n, n Z; б) ?n, n
Z; б) ?n, n Z; в)
Z; в)  ±
± +?n, n
+?n, n Z; г)
Z; г) 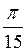 ±
± 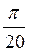 +
+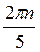 , n
, n Z.
Z.
2. a) cos x cos 3х = sin 3x sіn x;
Б) cos 2x cos х + sin 2x sin х = 1;
В) cos2 х – sin2 х = 0,5;
Г) 2sin2x = 1.
Відповідь: а) 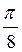 +
+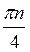 , n
, n Z; б) 2?n, n
Z; б) 2?n, n Z; в) ±
Z; в) ± +?n, n
+?n, n Z; г)
Z; г)  +
+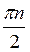 , n
, n Z.
Z.
3. а) 6соз2х + cos x – 1 = 0;
Б) cos x + 3cos х = 0;
В) 4cos2x – 3 = 0;
Г) cos2х = 1 + sin2x.
Відповідь: а) ± 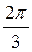 + 2?n; ± arccos
+ 2?n; ± arccos 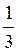 + 2?n, n
+ 2?n, n Z; б)
Z; б)  + ?n, n
+ ?n, n Z; в) ±
Z; в) ± + 2?n і ±
+ 2?n і ± 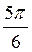 + 2?n, n
+ 2?n, n Z; г)
Z; г) 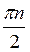 , n
, n Z.
Z.
4. а) (1 + cos x)(3 – 2cos x) = 0;
Відповідь: а) n + 2?n, n Z.
Z.
V. Підсумок уроку
VI. Домашнє завдання
Розділ II § 2 (2). Запитання і завдання для повторення до розділу II № 13-15. Вправи № 1 (9; 10; 13), № 2 (2; 4; 7).