Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції
УРОК 23
Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції
Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб).
І. Перевірка домашнього завдання
1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань.
2. Самостійна робота.
Розв’яжіть рівняння:
A) cosx =  . (3 бали)
. (3 бали)
Б) tg (х + 2) = 0. (3 бали)
В) 1 + ctg4x = 0. (3 бали)
Г) 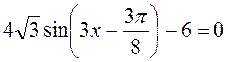
Розв’яжіть рівняння:
A) sinx =  . (3 бали)
. (3 бали)
Б) ctg (х – 3) = 0 . (3 бали)
В)  – tg2x = 0. (3 бали)
– tg2x = 0. (3 бали)
Г) 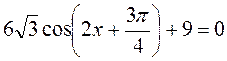 . (3 бали)
. (3 бали)
Відповіді: В-1. а) розв’язків немає; б) – 2 + ?n, n Z; в)
Z; в) 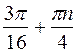 , n
, n Z; г)
Z; г) 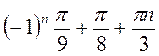 , n
, n Z.
Z.
В-2. а) розв’язків немає; б) 3 +  + ?n, n
+ ?n, n Z; в)
Z; в)  +
+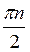 , n
, n Z; г) ±
Z; г) ± 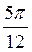 –
– 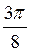 + ?n, n
+ ?n, n Z.
Z.
II.
Деякі тригонометричні рівняння шляхом тотожних перетворень можна привести до рівнянь з однією тригонометричною функцією, потім зробити заміну і привести рівняння до алгебраїчного.
Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння sin2х + 4cos x = 2,75.
Замінивши sin2х на 1 – cos2x, матимемо:
1 – cos2x + 4cos х – 2,75 = 0,
– cos2х + 4 cos х – 1,75 = 0,
Cos2 х – 4cos х + 1,75 = 0.
Нехай cos х = t, тоді t2 – 4t + 1,75 = 0.
Звідси t1 =  . t2 =
. t2 = 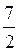 >1.
>1.
Оскільки t2 > 1, то cos x = 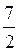 – розв’язків немає.
– розв’язків немає.
Оскільки t1 =  , то cos х =
, то cos х =  , х = ±
, х = ±  + 2 ?n, n
+ 2 ?n, n Z.
Z.
Відповідь: ±  + 2 ?n, n
+ 2 ?n, n Z.
Z.
Приклад 2. Розв’язати рівняння tg х + 3ctg х = 4.
Tg х + 3ctg х = – 4, tg х + 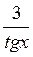 = 4.
= 4.
Нехай tg х = t, тоді t + 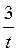 = 4, t2 – 4t + 3 = 0, t1 = 1 і t2 = 3.
= 4, t2 – 4t + 3 = 0, t1 = 1 і t2 = 3.
Маємо: 1) tg x = 1, х =  + ?n, n
+ ?n, n Z.
Z.
2) tg х = 3, х = arctg 3 + ?n, n Z.
Z.
Відповідь:  + ?n, arctg3 + ?n, n
+ ?n, arctg3 + ?n, n Z.
Z.
III. Формування умінь і навичок учнів розв’язувати тригонометричні рівняння, що зводяться до алгебраїчних
Виконання вправ______________________________
Розв’яжіть рівняння.
1. а) 2sin2x + cos х – 1 = 0;
Б) tg х – 2ctg х + 1 = 0;
В) 6sin2x + 5cos х – 2 = 0;
Г) tg x + 2ctg х = 3.
Відповідь: а) 2?n, ± 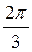 + 2 ?n, n
+ 2 ?n, n Z; б)
Z; б)  + ?n, – arctg 2 + ?n, n
+ ?n, – arctg 2 + ?n, n Z; в) ±
Z; в) ±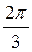 + 2?n,
+ 2?n,  Z; г) arctg 2 + ?n,
Z; г) arctg 2 + ?n,  + ?n, n
+ ?n, n Z.
Z.
2. a) cos 2х + sin x = 0;
Б) cos 2х = 3 + 7cos x;
В) 3 + 5sin 3х = cos 6х;
Г) 3cos2 6х + 8sin 3х cos 3х – 4 = 0.
Відповідь: а)  + 2?n, (-1)n+1
+ 2?n, (-1)n+1 + ?n, n
+ ?n, n Z; б) ±
Z; б) ± 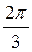 + 2 ?n, n
+ 2 ?n, n Z; в) (-1)n+1
Z; в) (-1)n+1 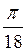 +
+ 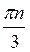 , n
, n Z; г)
Z; г) 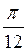 +
+ 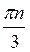 ,
, 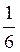 (-1)narcsin
(-1)narcsin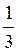 +
+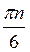 n
n Z.
Z.
IV. Підсумки уроку
V. Домашнє завдання
Розділ II § 3 (1). Вправи: № 2 (13; 23; 30; 37).