Головна ⇒ 📌Довідник з геометрії ⇒ Симетрія відносно прямої
Симетрія відносно прямої
Геометрія
Рух
Симетрія відносно прямої
Нехай а – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр AX на пряму а. На продовженні цього перпендикуляра за точку А відкладемо відрізок 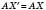 . Точка
. Точка 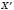 називається Симетричною точці X відносно прямої А.
називається Симетричною точці X відносно прямої А.
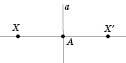
Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно прямої а.
Очевидно, що точка, симетрична точці 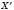 , є точка X.
, є точка X.
Перетворення фігури
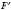 , при якому кожна точка X фігури F переходить у точку
, при якому кожна точка X фігури F переходить у точку 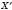 , симетричну відносно даної прямої а, називається Перетворенням симетрії відносно прямоїА. Отримані фігури називаються Симетричними відносно прямоїА.
, симетричну відносно даної прямої а, називається Перетворенням симетрії відносно прямоїА. Отримані фігури називаються Симетричними відносно прямоїА.Якщо перетворення симетрії відносно прямої а переводить фігуру F у себе, то така фігура називається Симетричною відносно прямоїА.
На рисунках наведені приклади осей симетрії фігур.
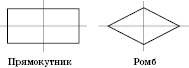
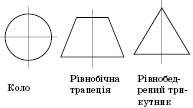
Теорема. Перетворення симетрії відносно прямої є рухом.
Related posts:
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Симетрія відносно прямої УРОК № 35 Тема. Симетрія відносно прямої Мета уроку: формування поняття симетрії відносно прямої; вивчення властивостей симетрії відносно прямої; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно прямої; будує фігури, у які переходять дані […]...
- Симетрія відносно точки УРОК № 34 Тема. Симетрія відносно точки Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані […]...
- Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...
- Поворот і симетрія відносно прямої 373. Із т. А опустимо перпендикуляр AD + l. Відкладемо ∠ΑΟΛ, = α, А1O + l. Виконано поворот т. А навколо прямої l на кут α. Аналогічно вчинимо з т. В. Відрізок АВ у результаті повороту на кут α навколо прямої l відобразиться у відрізок. 374. Таких поворотів безліч. 375. Точка А(1; 2; 0) відобразиться […]...
- Симетрія відносно площини 334. Якщо відрізок належить площині α, то відрізок симетричний сам собі. Якщо відрізок не лежить в площині: А) Відрізок паралельний площині α АА1 + α; АО = ОА 1 ВВ1 + α; BN = NB, A1В1 симетричний АВ відносно α; Б) Відрізок перетинає площину α. Відрізок А1В1 симетричний відрізку АВ відносно α. 335. Δ А1 […]...
- Подібність фігур Геометрія Подібність фігур Перетворення фігури F у фігуру називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів. Якщо відстані змінюються у k разів, то k називається Коефіцієнтом подібності. Якщо , перетворення подібності є рухом. Нехай F – дана фігура й О – фіксована точка. Через довільну […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Поняття про рух, рівність фігур у просторі Урок 48 Тема. Поняття про рух, рівність фігур у просторі Мета уроку: формування понять: рух, рівні фігури. Доведення нової властивості руху: площина під час руху переходить у площину. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 48), модель куба. Хід уроку 1. Відповісти на запитання учнів, які виникли […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Урок 13 Тема. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини. Обладнання: стереометричний набір, моделі куба і тетраедра, схема “Аксіоми стереометрії”. Хід уроку І. Аналіз виконання тематичного оцінювання № 1. Зібрати зошити наприкінці […]...
- Поворот УРОК № 36 Тема. Поворот Мета уроку: формування поняття повороту та вивчення властивостей повороту; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують поворот; будує фігури, у які переходять дані фігури при повороті; застосовують вивчені означення і […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Перетворення подібності та його властивості Урок 50 Тема. Перетворення подібності та його властивості Мета уроку: формування знань учнів про подібність просторових фігур, вивчення властивостей перетворення подібності та застосування їх до розв’язування задач. Обладнання: моделі куба і тетраедра. Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення контрольних запитань № 9-11 та розв’язування задач № 23-25 (1). 2. Математичний диктант. При […]...
- Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...
- Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Урок 8 Тема. Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Мета уроку: вивчення теореми про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Які прямі в просторі називаються паралельними? 2) Вкажіть […]...
- Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Урок 27 Тема. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Мета уроку: формування поняття прямої, перпендикулярної до площини. Вивчення ознаки перпендикулярності прямої і площини. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Відповіді на запитання, які виникли в учнів при виконанні домашнього завдання. 2. Самостійна робота. Варіант 1 1) Промені OВ, ОС, OD […]...
- Паралельне перенесення УРОК № 37 Тема. Паралельне перенесення Мета уроку: формування поняття паралельного перенесення та вивчення властивостей паралельного перенесення; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують паралельне перенесення; будують фігури, у які переходять дані фігури при паралельному […]...
- Паралельне перенесення та його властивості Геометрія Рух Паралельне перенесення та його властивості Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b – одні й ті самі для всіх точок, називається Паралельним перенесенням. Теорема. Паралельне перенесення є рухом. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе) (див. рисунок). Існування […]...
- Властивості прямої і площини, перпендикулярних між собою Урок 30 Тема. Властивості прямої і площини, перпендикулярних між собою Мета уроку: формування знань учнів про властивості перпендикулярних прямих і площин. Обладнання: стереометричний набір, схема “Властивості прямо і площини, перпендикулярних між собою” (с. 116). Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення розв’язування задачі № 10. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Перетин прямої з площиною. Перерізи многогранників УРОК 3 Тема. Перетин прямої з площиною. Перерізи многогранників Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір. 1. Фронтальне опитування. 1) Скільки площин визначають дві прямі, які перетинаються? 2) […]...
- Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...
- Перетворення простору 1. 1) Вектор паралельного перенесення, що переводить відрізок ОА в СВ: Вектор, що переводить відрізок ОС в АВ: 2) Вектор, що переводить ОС в АВ: Вектор, що переводить О А в СВ: 3) Вектор, що переводить ОС в АВ: Вектор, що переводить ОА в СВ: 4) Вектор, що переводить ОС в АВ: Вектор, що переводить […]...
- Геометричні перетворення у просторі. Рухи 306. Пряма і площина відображуються на себе відносно будь-якої точки, що належить їм. 307. Два нерівні відрізки бути симетричними відносно деякої точки не можуть. 308. Відносно початку координат: Точці А(1; -3; 2) симетрична A1(-1; 3;-2); Точці В(-5; 0; 2) – B1(5; 0; -2); Точці С(3; -1; 0) – С1 (-3; 1; 0); Точці D(0; 0; […]...
- Перпендикуляр до прямої Урок № 19 Тема. Перпендикуляр до прямої Мета: домогтися розуміння учнями змісту теореми про існування та єдиність прямої, що проходить через будь-яку точку площини перпендикулярної даній; понять: “перпендикуляр, проведений з точки до прямої”, “відстані від точки до прямої”. Сформувати вміння: – відтворювати зміст зазначеної теореми та застосовувати її під час розв’язування задач; – на рисунку […]...
- Взаємне розміщення кола і прямої – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення кола і прямої Коло і пряма не мають спільних точок. Коло і пряма мають одну спільну точку. А – дотична А – точка дотику Коло і пряма мають дві спільні точки. А – січна Рівняння кола (х – а)2 + (y – b)2 = R2, де (а, b) […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Переміщення та його властивості. Рівні фігури УРОК № 33 Тема. Переміщення та його властивості. Рівні фігури Мета уроку: формування поняття переміщення та рівних фігур; вивчення властивостей переміщення. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур”. Рухи” [13]. Вимоги до рівня підготовки учнів: описують рівність фігур; будують фігури, у які переходять дані фігури при переміщеннях; формулюють властивості переміщення; застосовують вивчені означення […]...