Головна ⇒ 📌ГДЗ з математики ⇒ Складніші задачі на побудову

Складніші задачі на побудову

Розділ 1. Найпростіші геометричні фігури та їх властивості

§ 19. Складніші задачі на побудову

736. Так.

737. Мал. 401. X належить бісектрисі кута В та колу.

Мал. 402. X належить бісектрисі кута В та серединному перпендикуляру ОХ до відрізка ВС.

Мал. 403. X належить серединному перпендикуляру ВО до відрізка АС та колу.

738.

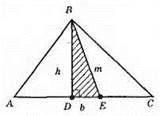
1) Спочатку будуємо трикутник BDE.

2) На прямій DE відкладемо від точки Е по різні боки рівні відрізки АЕ і ЕС.

3) ?ABC – шуканий.

739.

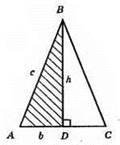
1) Спочатку будуємо

прямокутний трикутник ВDА за гіпотенузою с і катетом h.

2) На промені AB від точки А відкладемо АС = b.

3) ?АВС – шуканий.

740.

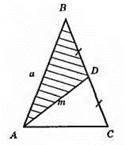
1) Будуємо трикутник АВD за трьома сторонами AB = a, AD = m, BD = a/2.

2) На промені BD від точки D відкладемо DC = a/2.

3) ?АВС – шуканий.

741.

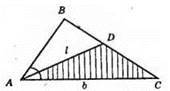
1) Будуємо? АDС за двома сторонами AD = l, АС = b і кутом між ними ∠DАС = α/2.

2) Будуємо кут ∠BAD = α/2. Точка В – точка перетину сторони AB кута ВАD і продовження сторони ВС.

3) ?АВС – шуканий.

742.

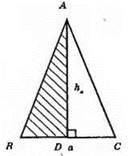
1) Будуємо прямокутний трикутник ABD за двома катетами: BD

= a/2 і АD = ha.

2) На промені BD від точки D відкладемо DC = a/2.

3) ?АВС – шуканий.

Оскільки AD – висота і медіана трикутника ABC, то? ABC – рівнобедрений, в якому AD = hа, ВС = а.

743.

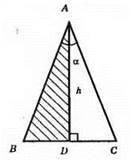
1) Будуємо прямокутний трикутник АВD за катетом AD = h і гострим кутом ∠BAD = α/2.

2) На промені ВD від точки D відкладемо DС = ВD.

3) ?АВС – шуканий.

Оскільки AD – висота і медіана трикутника ABC, то? АВС – рівнобедрений, в якому AD = h, оскільки AD – бісектриса, то ∠ВАС = α.

744.

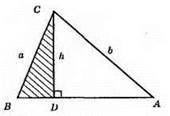
1) Будуємо прямокутний ДBCD за гіпотенузою ВС = а і катетом CD = h.

2) Знаходимо точку А – як точку перетину променя BD та кола з центром у точці С і з радіусом b.

3) ?АВС – шуканий.

Оскільки ВС = а, CA = b, CD ⊥ AB, CD = h, то? АВС – шуканий.

745.

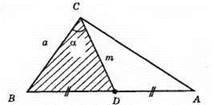
1) Будуємо ABCD за двома сторонами: ВС = a, CD = m і кутом між ними ∠BCD = α.

2) На промені BD від точки D відкладемо DA = BD.

3) ?АВС – шуканий, оскільки ВС = а, ∠BCD = α, BD = DA, CD = m.

746.

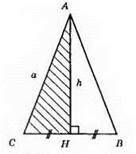
1) Будуємо прямокутний трикутник АСН за гіпотенузою АС = b і катетом АН = h.

2) На промені СH від точки H відкладемо HВ = СH.

3) ?АВС – шуканий.

Оскільки АН – висота і медіана, то? АВС – рівнобедрений, в якому АС = AB = b, АН ⊥ ВС, АН = h.

747.

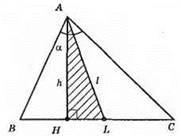
1) Будуємо прямокутний трикутник AHL за гіпотенузою AL = l і катетом АH = h.

2) Від променя AL в різні боки будуємо кути ∠LAB = α/2 і ∠LAC = α/2.

3) Точки В і С – точки перетину сторін AB і АС побудованих кутів та продовження сторони HL трикутника АHL.

4) ?ABC – шуканий, оскільки АН ⊥ ВС, ∠BAL = ∠LAC, AL = l, ∠BAC = α.

748. 1) Будуємо? ADC (мал. 408) за трьома сторонами: АС = b, CD = с, AD = 2m.

2) Ділимо сторону AD пополам (точка М – середина AB).

3) На промені CM від точки М відкладемо MB = СМ.

4) ?АВС – шуканий.

749. 1) Будуємо коло з центром у точці О і з радіусом В.

2) 3 довільної точки А кола будуємо коло радіуса b, яке перетне побудоване коло в точці С.

3) Ділимо відрізок АС пополам (В – середина АС).

4) Із точки В будуємо коло з радіусом m, яке перетне початкове коло в точці В.

5) ?АВС – шуканий.

750.

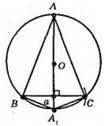
1) Будуємо коло з центром О і з радіусом R.

2) 3 довільної точки кола В будуємо коло з радіусом а, яке перетне побудоване коло в точці С.

3) Будуємо серединний перпендикуляр OD, який перетне початкове коло в точках А і А1.

4) ?АВС і? A1BC – шукані.

751. 1) Будуємо коло з центром О і з радіусом R.

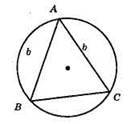
2) 3 довільної точки А кола будуємо коло радіуса b, яке перетне побудоване коло в точках В і С.

3) ?АВС – шуканий.

752.

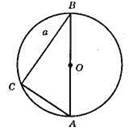
1) Будуємо коло з центром О і з радіусом R.

2) 3 довільної точки В кола будуємо діаметр ВА і коло радіуса а, яке перетне побудоване коло в точці С.

3) ?АВС – шуканий.

753.

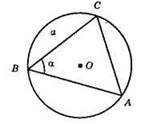
1) Будуємо коло з центром О і з радіусом R.

2) 3 довільної точки В кола будуємо коло з радіусом а, яке перетне побудоване коло в точці С.

3) Від променя ВС відкладемо кут ∠CBA = α, сторона якого перетне коло в точці А.

4) ?АВС – шуканий.

754.

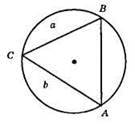
1) Будуємо коло з центром О і з радіусом R.

2) 3 довільної точки С кола будуємо коло радіуса а, яке перетне побудоване коло в точці В, та коло радіуса b, яке перетне початкове коло в точці А.

3) ?АВС – шуканий.

755.

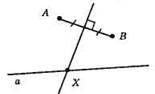
Шукана точка X – точка перетину серединного перпендикуляра до відрізка AB та даної прямої а.

756. Шукана точка Х – точка перетину серединного перпендикуляра до відрізка AB та даного кола. Задача має:

1) або два розв’язки;

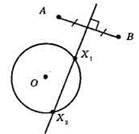
2) або один розв’язок;

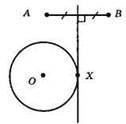
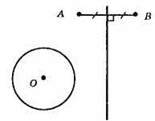
3) або жодного.

757. Шукана точка Х – точка перетину прямої ВС, яка перетинає сторони кута А та бісектриси АХ кута А.

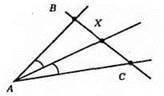
758. Шукана точка Х – точка перетину кола і бісектриси BD даного кута ABC. Таких точок може бути:

1) Дві.

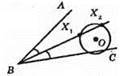
2) Одна.

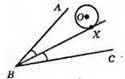
3) Жодної.

759.

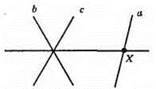
Шукана точка X – точка перетину прямої, що містить бісектрису утворених кутів, та даної прямої а. Задача може мати:

1) Один розв’язок.

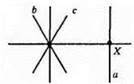
2) Два розв’язки.

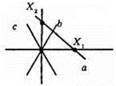
3) безліч розв’язків.

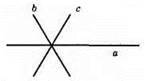
760. Шукана точка Х – точка перетину даної прямої а і кола з центром у точці А і радіусом m. Задача може мати:

1) Два розв’язки.

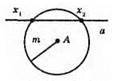
2) Один розв’язок.

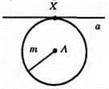
3) Жодного.

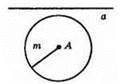
761.

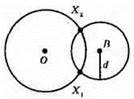
Шукана точка X – точка перетину кола радіуса d з центром в т. В із даним колом.

762.

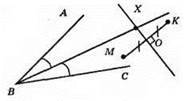
Шукана точка X – точка перетину бісектриси кута ABC та серединного перпендикуляра до відрізка МК.

763.

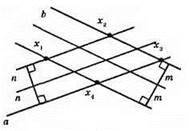
Шукані точки X – точки перетину прямих, які паралельні до а і знаходяться від прямої а на відстані n, та прямих, які паралельні b і знаходяться від прямої b на відстані m.

764.

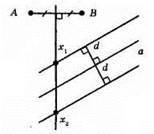
Шукані точки X – точки перетину серединного перпендикуляра до відрізка AB та прямих, які паралельні до прямої а і знаходяться на відстані d від неї.

765.

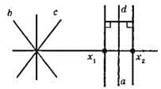
Шукані точки X – точки перетину прямих, що містять бісектриси кутів, що утворилися при перетині прямих b і с та прямих, які паралельні прямій а і знаходяться на відстані d від неї.

766.

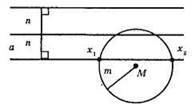
Шукані точки X – точки перетину прямих, які паралельні до прямої а і знаходяться на відстані n від неї, та кола з центром у точці М та з радіусом m. Таких точок може не бути, або таких точок може бути 1, 2, 3, 4.

767. 1) Через точку В проводимо перпендикуляр OB до прямої а.

2) Проводимо серединний перпендикуляр до відрізка AB, який перетинає побудований перпендикуляр у точці О.

3) Коло з центром О і з радіусом OB = ОА є шуканим.

768.

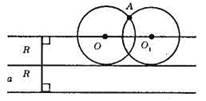
1) Будуємо прямі, які паралельні прямій а і знаходяться від неї на відстані R.

2) Будуємо коло з центром у точці А і радіусом R, яке перетне дані прямі (наприклад у точках О і O1).

3) Будуємо коло з центром у точці О (O1), радіуса R, воно є шуканим.

769. 1) Будуємо бісектрису BF кута ABC.

2) Проводимо перпендикуляр через точку D до прямої ВС.

3) Знаходимо точку О перетину бісектриси та перпендикуляра.

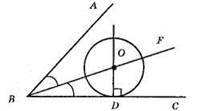
4) Проводимо коло з центром у точці О і з радіусом OD, воно є шуканим.

770.

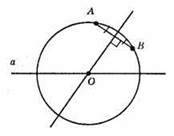
1) Будуємо серединний перпендикуляр до відрізка AB, який перетинає дану пряму а в точці О.

2) Будуємо коло з центром у точці О і радіусом ОА = OB, воно є шуканим.

771.

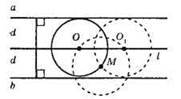
1) Будуємо пряму l, яка лежить між прямими а і b на однаковій відстані d від них.

2) Будуємо коло з центром у точці М і з радіусом d, яке перетне пряму l у точках О і О1.

3) Будуємо кола з центрами О і O1 і з радіусом d, вони і будуть шуканими.

772. 1) Будуємо прямокутний трикутник ВКС за гіпотенузою ВС = а та катетом BK = h.

2) Ділимо сторону ВС навпіл (точка D – середина ВС).

3) Точку А знаходимо як перетин променя СК та кола з центром у точці D і радіусом m.

4) ?ABC – шуканий.

773.

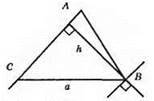
1) Будуємо кут А.

2) Проводимо пряму b, яка паралельна стороні АС і знаходиться на відстані h від неї. Ця пряма перетне другу сторону кута в точці В.

2) Точку С знаходимо як точку перетину променя АС та кола з центром у точці В і з радіусом.

4) ?ABC – шуканий.

774. 1) Будуємо прямокутний трикутник за катетами (мал. 412) ВС = а, CD = b + с.

2) Проводимо серединний перпендикуляр до сторони BD, який перетинає сторону CD в точці А.

3) ?ABC – шуканий.

Оскільки точка А належить серединному перпендикуляру, то AD = ВС = с, тоді АС = b, ВС = а.

775.

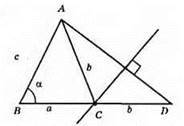
1) Будуємо? ABD за двома сторонами: AB = с і BD = а + b і кутом ∠B = а.

2) Проводимо серединний перпендикуляр до сторони AD, який перетинає сторону BD і точці С.

3) ?ABC – шуканий.

776.

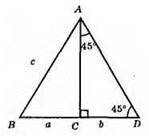
1) Будуємо? BAD за двома сторонами AB = с, BD = а + b, та кутом D, що лежить проти сторони С. ∠D = 45°.

2) В? BAD із вершини А опускаємо перпендикуляр АС.

3) ?АВС – шуканий.

777.

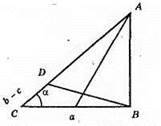
1) Будуємо? CBD, у якого СВ = а, CD = b – c, ∠С = а.

2) Точку А знаходимо як точку перетину променя CD та серединного перпендикуляра до сторони BD.

3) ?АВС – шуканий.

Застосуйте на практиці

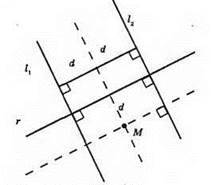
Базу відпочинку М треба розмістити на перетині прямої, яка паралельна автомагістралі l1 і l2 і знаходиться від них на однаковій відстані d, та прямої, яка паралельна річці r і знаходиться від неї на відстані d.

Тестові завдання

1.1. Г; 2. Г; 3. Г; 4. Б; 5. В.

2.1. Г; 2. В; 3. В; 4. Б; 5. В.