Урок узагальнення та систематизації знань з теми “Багаточлени”
Урок № 41
Тема. Урок узагальнення та систематизації знань з теми “Багаточлени”
Мета: повторити, узагальнити та систематизувати знання та вміння учнів, які вони дістали з теми “Багаточлени”.
Тип уроку: систематизація та узагальнення знань.
Хід уроку
I. Перевірка домашнього завдання
@ Для перевірки домашнього завдання вчитель збирає зошити, але оскільки аналіз самостійної роботи необхідний (тим більше, що учні отримали завдання виписати ті вправи, що викликали труднощі) , то можна після збору зошитів запропонувати
II. Робота з випереджальним домашнім завданням. Повторення і систематизація знань
Контрольні запитання
1. Дайте означення багаточлена.
2. Який багаточлен називається багаточленом стандартного вигляду?
3. Що треба зробити, щоб даний багаточлен звести до стандартного вигляду?
4. Усі члени багаточлена мають стандартний вигляд. Чи можна зробити висновок, що багаточлен має стандартний вигляд?
5. Серед членів багаточлена немає подібних. Чи з цього випливає, що багаточлен має стандартний вигляд?
6. Що є степенем багаточлена
7. Як розкрити дужки, перед яким стоїть знак “+” (“-“)?
8. Сформулюйте, як заключити доданки в дужки.
9. Сформулюйте правило множення одночлена на багаточлен.
10. Яка властивість використовується під час множення одночлена на багаточлен?
11. Чи будь-який добуток одночлена на багаточлен можна подати у вигляді багаточлена?
12. Що називається розкладанням багаточлена на множники?
13. Яка властивість багаточлена використовується під час винесення спільного множника за дужки?
14. Сформулюйте правило множення багаточлена на багаточлен.
15. Скільки членів (до зведення подібних) повинен містити багаточлен, що утворюється під час множення багаточлена, що містить п членів, на багаточлен, що містить т членів?
16. В якій послідовності виконується розкладання багаточлена на множники способом групування?
@ Оскільки випереджальним домашнім завданням було передбачено повторення виділеного матеріалу, то завдання учнів полягає в тому, щоб здійснити самоконтроль щодо визначених термінів та їх розуміння. Після самоперевірки обговорюємо зміст понять.
III. Повторення, узагальнення та систематизація вмінь
Розв’язування вправ
@ Завдання розбиваємо на блоки за основними темами:
1) Додавання та віднімання багаточленів.
2) Множення одночлена на багаточлен; багаточлена на багаточлен.
3) Розкладання багаточлена на множники.
Блок І
1. Спростіть вираз:
1) 14а + 8b – (а + 8b – 7);
2) (8х2 – 12х + 4) – (2х2 + 5x – 2);
3) 
.
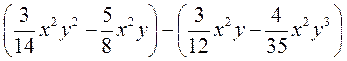2. Доведіть, що різниця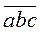 
і 
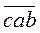кратна 9.
3. Подайте багаточлен 2у2 +4у – 5 у вигляді різниці двох двочленів.
Блок II
1. Спростіть вираз:
1) -3b(a2 + 6ab + 5b); 2) 0,4аb2(2а2b – 5аb +7а2b2);
3) 5х(х – 4) – 2(х2 + 3х); 4) 4b(2b2 – 5а) – 9b(b +3а) + 6b(-2а + 5b).
2. Перетворіть у багаточлен:
1) (3х – 5)(2х + 7);
3. 2) (х + 3)(х – 7) – 4х(5 – 2х);
3) (z – 3)(3z + 1) – (2z + 3)(4z – 1).
4. Розв’яжіть рівняння (3х + 5)(2х + 1) = (6х + 5)(х – 3) + 4.
5. Знайдіть три послідовних натуральних числа, якщо добуток другого та третього на 47 більший за квадрат першого.
Блок III
1. Розкладіть на множники:
1) 3а – 15b;
2) 6а2 – 12аb;
3) 4(а – b) + с(а – b);
4) ху – хz + ту – тz;
5) х2 – 4х – 21.
2. Розв’яжіть рівняння:
1) х2 + 7х = 0;
2) х(х – 7) + 3(х – 7) = 0.
IV. Підсумки уроку
1. Виділяємо основні питання, винесені для перевірки на тематичну контрольну роботу.
2. Учні отримують завдання самоактуалізуватися (тобто повторити ті питання зі списку, що викликають у них труднощі).
V. Домашнє завдання
Домашня контрольна робота або творче завдання
1) Складання схем-алгоритмів виконання дій з багаточленами;
2) складання задач (на подільність, на визначення останньої цифри, на складання рівняння тощо);
3) складання кросвордів, сканвордів, математичних казок.
Умова домашньої контрольної роботи
№ 1. Запишіть у вигляді багаточлена стандартного вигляду:
1) 3(4а – 1) – 2(12а + 3) + 2а;
2) х2 – 2х – 8 – (2х2 + х – 7);
3) 2х7(3х2 – x + 1);
4) (3a – 2b)(2a – 5b);
5) 2х3у2(-1,6х4у3 + 3,4х2у);
6) (a – 4b)(2a2 + ab – 2b2); 7) (2х2 – 4х + 3)(х2 + х + 1).
№ 2. Розкладіть на множники:
1) 4х – 12х2;
2) 2а2b + 4а3b – 2а4b;
3) а2m + х2 – аmх – ах.
№ 3. Доведіть, що:
1) вираз (k + 1)(k2 – k + 1) – k(k2 – 4 k – 4) набуває лише додатних значень;
2) значення виразу 312 + 311 – 95 ділиться 11;
3) 4n + 22n+2 + 4n+2 ділиться на 21 при будь-якому натуральному n.
№ 4. Розв’яжіть рівняння:
1) х(3 + х) – х2 = 6; 2) х – 2х2 = 0; 3)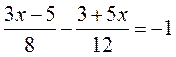 
;
4) (2х – 3)(3х + 2) = (2х + 3)(х – 2); 5) х3 + 6х2 + 2х + 12 = 0.
(1 votes, average: 5.00 out of 5)
Loading...