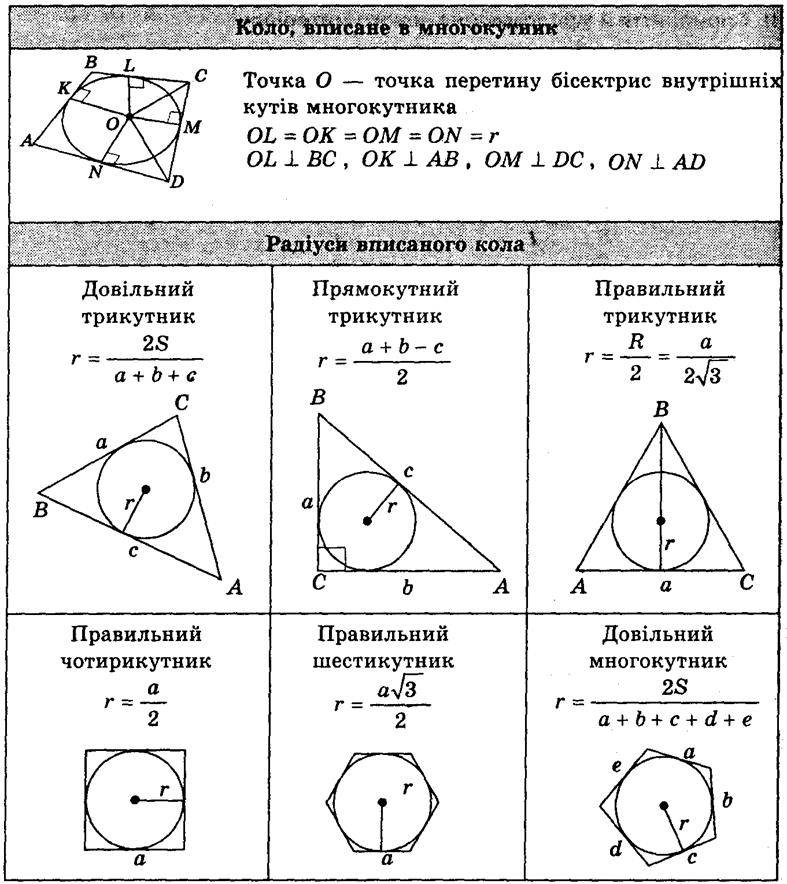
Властивість точки, рівновіддаленої від сторін многокутника
Урок 36
Тема. Властивість точки, рівновіддаленої від сторін многокутника
Мета уроку: формування вмінь учнів застосовувати властивість ортогональної проекції точки, рівновіддаленої від сторін многокутника, до розв’язування задач.
Обладнання: стереометричний набір, схема “Коло, вписане в многокутник”
Хід уроку
1. Перевірити правильність виконання вправ № 42, 48, 53 за записами, зробленими на дошці до початку уроку.
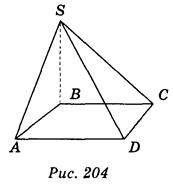
Нехай ABCD – прямокутник; BS
(АВС); SD = с, SC = b, SA = a (рис. 204).
Оскільки ВС
CD. Із? SDC DC =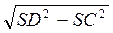
= 
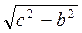.Оскільки ВАAD, то SAAD. Із? SAD AD =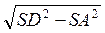 
= 
.
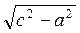Із? SAB SB =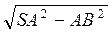 
= 
= 
.
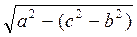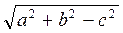Відповідь. ; ; .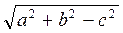
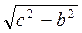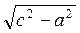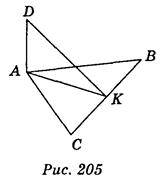
Нехай АВС – рівносторонній трикутник; ВС = 6 см; AD(АВС); AD = 13 см (рис. 205). Проведемо АКВС, тоді DKВС; отже,
Із? АСА АК =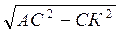 
= 
= 
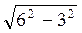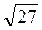(см).
Із? ADA DK =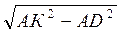 
= 
= 
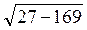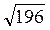= 14 (см).
Відповідь. 14 см.
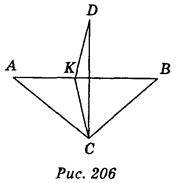
Нехай у? АВС (
С = 90°) AB = а, ВС = b; CD(ABC); CD = c (рис. 206). Проведемо CKAB, тоді DKAB; отже, DK – відстань від точки D до прямої AB.
Із? АВС AC =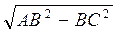 
=
.
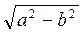S =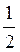 
ВС – АС = 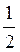B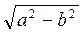, або S=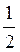AB – CK= 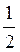A – CK, то 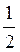B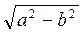=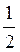A – CK; CK = 
.
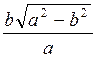Із? CDK DK=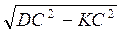
=
=
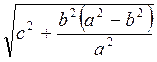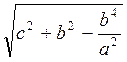
Відповідь. .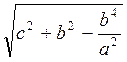
2. Самостійна робота.
Варіант. 1
1) Відрізок SC перпендикулярний до площини рівностороннього трикутника АВС. Проведіть через точку S перпендикуляр до прямої АВ. (4 бали)
2) Через точку О перетину діагоналей ромба до його площини проведено перпендикуляр OS довжиною 5 см. Знайти відстань від точки S до кожної сторони ромба, якщо діагоналі ромба дорівнюють 40 і 30 см. (8 балів)
1) Відрізок SA перпендикулярний до площини рівнобедреного трикутника АВС, в якому АВ = AC. Проведіть через точку S перпендикуляр до прямої ВС. (4 бали)
2) Катети прямокутного трикутника АВС дорівнюють 9 і 12 см. Через середину гіпотенузи – точку О проведено перпендикуляр до площини трикутника довжиною 6 см. Знайдіть відстані від кінців перпендикуляра до катетів. (8 балів)
1) Відрізок SD перпендикулярний до площини прямокутника ABCD. Проведіть через точку S перпендикуляри до ВС і АВ. (4 бали)
2) Сторона правильного трикутника АВС дорівнює 2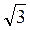
см. До площини трикутника проведено перпендикуляр AS довжиною 4 см. Знайдіть відстань від точки S до сторони ВС. (8 балів)
Варіант 4
1) Відрізок SA перпендикулярний до площини ромба ABCD. Проведіть через точку S перпендикуляр до прямої BD. (4 бали)
2) До площини прямокутного трикутника ABC (C = 90°) проведено перпендикуляр SB, SA = 13 см, B = 30°, AC = 5 см. Знайдіть відстань від точки S до прямої АС. (8 балів)
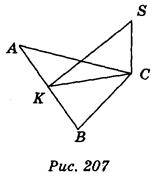
Відповідь. Варіант 1. 1) СКАВ, тоді SKАВ (рис. 207); 2) 13 см.
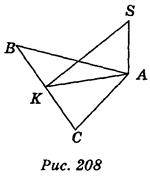
Варіант 2. 1) АKВС, тоді SKВС (рис. 208); 2) 7,5 см і 6
См.
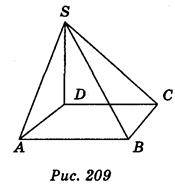
Варіант 3. 1) Оскільки DCCB і DA AB, то SCВС, SAАВ (рис. 209); 2) 5 см.
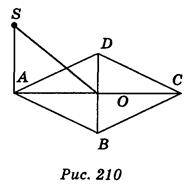
Варіант 4. 1) Оскільки ACBD, то SOAD (рис. 210); 2) 12 см.
Властивість точки, рівновіддаленої від сторін многокутника
Розв’язування задачі № 45 (с. 37) із підручника. Після розв’язування цієї задачі слід зробити висновок і записати його в зошити учнів:
Якщо через центр кола, вписаного в многокутник, проведено перпендикуляр до площини многокутника, то кожна точка перпендикуляра рівновіддалена від сторін многокутника.
Теорема.
Якщо точка рівновіддалена від сторін многокутника і основа. перпендикуляра, опущеного з даної точки до площини многокутника, лежить всередині многокутника, то основа перпендикуляра є центром кола, вписаного в многокутник.
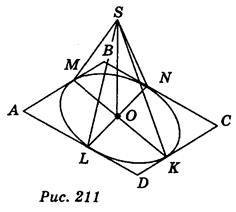
Нехай К, L, М, N – основи перпендикулярів, опущених з точки S на сторони CD, DA, АВ, ВС плоского чотирикутника ABCD (рис. 211), і SO(АВС), SK=SL=SM=SN. ?SOК=?SLO=?SMO=?SNO (за гіпотенузою і спільним катетом OS); із рівності трикутників випливає OK =QL = ОМ = ON (1).
Оскільки SKDC, SLAD, SMAB, SNBC, то за теоремою про три перпендикуляри маємо: OKDC, OLAD, ОМAB, ONBC (2).
Враховуючи (1) і (2), робимо висновок: точка О – центр кола, вписаного в чотирикутник ABCD.
Далі слід нагадати формули для знаходження радіуса кола, вписаного в многокутники, за допомогою наведеної схеми.
Розв’язування задач
1. Точка О – центр квадрата зі стороною 4 см, АО – пряма, що перпендикулярна до площини квадрата, АО = 2См. Знайдіть відстань від точки А до сторін квадрата.
2. Відстань від точки S до сторін квадрата дорівнює 13 см. Знайдіть відстань від точки S до площини квадрата, якщо сторона квадрата дорівнює 10 см.
3. Точка S на 5 см віддалена від усіх сторін правильного трикутника, медіана якого дорівнює 9 см. Знайдіть відстань від даної точки до площини трикутника.
4. Відстань від точки S до сторін правильного трикутника дорівнює 10 см. Знайдіть відстань від точки S до площини трикутника, якщо сторона трикутника дорівнює 16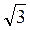 см.
III. Домашнє завдання
§3, п. 19; задачі № 46, 47 (с. 37-38).
Запитання до класу
1) Що називається відстанню від точки до прямої?
2) Яку властивість має Основа перпендикуляра, опущеного з точки, яка рівновіддалена від вершин многокутника.
3) Яку властивість має основа перпендикуляра, опущеного з точки, яка рівновіддалена від сторін многокутника, якщо основа перпендикуляра лежить всередині многокутника?
(1 votes, average: 5.00 out of 5)
Loading...