Властивості кутів, утворених при перетині двох паралельних прямих січною
Урок № 32
Тема. Властивості кутів, утворених при перетині двох паралельних прямих січною
Мета: закріпити знання учнів про зміст та схему доведення теореми про властивості кутів та наслідків з неї; сформувати уявлення учнів про відстань між двома паралельними прямими; сформувати вміння використовувати названі вище теоретичні відомості під час розв’язування задач на знаходження кутів при паралельних прямих та січній і відстані між паралельними прямими.
Тип уроку: застосування знань, умінь та навичок.
Наочність і обладнання:
ХІД УРОКУ
I. Організаційний момент
II. Перевірка домашнього завдання
Домашнє завдання перевіряємо за зразком взаємоперевіркою.
III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку
Для створення позитивної мотивації можна запропонувати учням до розв’язання проблему (створити проблемну ситуацію).
Як знайти відстань від точки A до точки B?
Як знайти відстань від точки A до прямої b? При якому взаємному розташуванні A і b може йти мова про відстань між ними?
Як знайти відстань від
Останнє запитання і спонукає учнів до вивчення питання, винесеного в тему уроку, і пошук відповіді на нього є по суті основною метою уроку.
IV. Актуалізація опорних знань
Виконання усних вправ
1. Знайдіть усі невідомі кути на рисунку 1, якщо a||b:
А) 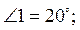
Б) 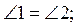
В) 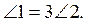
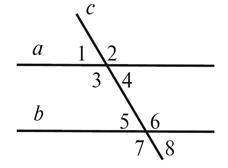
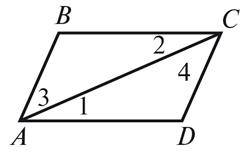
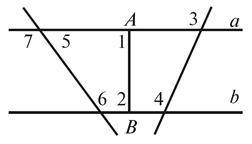
2. Дано: AB || CD, BC || AD (рис. 2).Доведіть, що 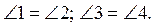
3. Укажіть взаємне розташування прямих b і c, якщо a||b, 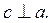
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Теорема про відстані від точок прямої до паралельної прямої (з доведенням).
2°. Означення відстані між паралельними прямими. Поняття спільного перпендикуляра до паралельних прямих.
Методичний коментар
На відміну від підручника О. В. Погорєлова, в якому твердження теореми винесено в опорну задачу (§ 4, № 50), підручник авторів А. П. Єршової та ін. містить це саме твердження у вигляді самостійної теореми, що напевно свідчить про досить важливе місце цього питання. Також новий підручник містить інший підхід до доведення (з посиланням на наслідок з теореми про властивість кутів, утворених при перетині паралельних прямих січною). Учитель також може звернути увагу на доречне в цьому місці поняття спільного перпендикуляра до двох паралельних прямих.
VI. Первинне усвідомлення нового матеріалу
Виконання усних вправ
Один із кутів, утворених у результаті перетину двох паралельних прямих січною, дорівнює 120°. Чи може один із решти семи кутів дорівнювати 50°? Чому?
Виконання письмових вправ
1. Прямі a і b паралельні. Точки A1 і A2 лежать на прямій a, відрізки A1B1 і A2B2 – відстані між прямими a і b. Назвіть відрізки, які є відстанями між прямими A1B1 і A2B2. Відповідь обгрунтуйте.
2. Відрізок AB – відстань між паралельними прямими a і b. Точка M – середина відрізка AB. Доведіть, що будь-який відрізок із кінцями на даних прямих, який проходить через точку M, ділиться нею навпіл.
VII. Засвоєння навичок
На уроці бажано приділити увагу розв’язанню задач на сумісне застосування ознак і властивостей паралельних прямих. Доцільно на уроці розв’язати типові для цієї теми задачі.
Рівень Б
За даними рисунка 3 знайдіть кут x.
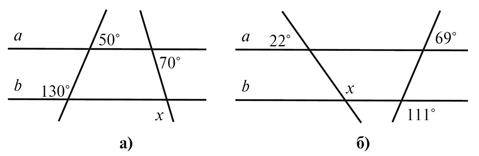
Рівень В
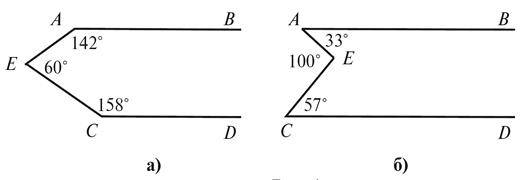
1. За даними рисунка 4, а, б визначте, чи паралельні прямі AB і CD.
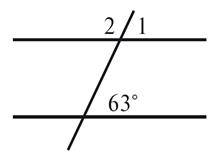
2. Бісектриси внутрішніх односторонніх кутів, утворених у результаті перетину двох паралельних прямих січною, взаємно перпендикулярні. Доведіть.
3. Бісектриси внутрішніх різносторонніх кутів, утворених у результаті перетину двох паралельних прямих січною, паралельні. Доведіть.
VIII. Підсумки уроку
На рисунку 5 AB – відстань між прямими a і b. Що можна сказати про кути, позначені на рисунку 5?
IX. Домашнє завдання
Вивчити теоретичний матеріал.
Розв’язати задачі.
1. За даними рисунка 6, визначте, чи паралельні прямі a і b, якщо 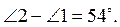
2. Через вершину B рівнобедреного трикутника ABC проведено пряму l, паралельну основі AC. Відрізок BK – медіана трикутника ABC. Доведіть, що BK – відстань між прямими l і AC.
3. Дано рівнобедрений трикутник ABC з основою AC. Пряма, паралельна AC, перетинає сторону AB у точці A1 , а сторону BC – у точці C1. Доведіть, що трикутник A1BC1 рівнобедрений.
Або учням можна запропонувати домашню самостійну роботу.
Домашня самостійна робота
Варіант 1
Початковий рівень
1. Різниця двох із восьми кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 54° . Знайдіть кожний із восьми кутів.
Середній рівень
2. Січна перетинає дві дані прямі; при цьому утворилися внутрішні односторонні кути, різниця яких дорівнює 108°, а відношення – 4 : 1. Доведіть, що дані прямі паралельні.
Достатній рівень
3. Відрізки AB і CD є паралельними й рівними. Доведіть, що Δ ABC = Δ DCB, якщо відрізки AD і BC перетинаються.
Високий рівень
4. Через точки A і B, що лежать на сторонах тупого кута AOB, проведено прямі, які паралельні сторонам даного кута й перетинаються в точці C. Знайдіть кут AOB, якщо прямі AC і BC перетинаються під кутом 40°.
Варіант 2
Початковий рівень
1. Сума двох із восьми кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 72° . Знайдіть кожний із восьми кутів.
Середній рівень
2. Січна перетинає дві дані прямі; при цьому утворилися внутрішні односторонні кути, різниця яких дорівнює 36°, а відношення – 3 : 2. Доведіть, що дані прямі паралельні.
Достатній рівень
3. Відрізки AB і CD є паралельними й рівними. Доведіть, що Δ AOB = Δ DOC, де O – точка перетину відрізків AD і BC.
Високий рівень
4. Кут AOB дорівнює 135°. Через точки A і B проведено прямі, які паралельні сторонам даного кута й перетинаються в точці C. Під яким кутом перетинаються ці прямі?
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.