Властивості перетворення подібності

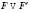Related posts:

1. Перетворення подібності та його властивості Урок 50 Тема. Перетворення подібності та його властивості Мета уроку: формування знань учнів про подібність просторових фігур, вивчення властивостей перетворення подібності та застосування їх до розв’язування задач. Обладнання: моделі куба і тетраедра. Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення контрольних запитань № 9-11 та розв’я­зування задач № 23-25 (1). 2. Математичний диктант. При […]...
2. Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
3. Подібність просторових фігур – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Подібність просторових фігур Перетворення фігури F називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюють себе в одну й ту саму кількість разів. Як і на площині, перетворення подібності в просторі переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими. […]...
4. Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...
5. Рівність фігур Геометрія Рух Рівність фігур Дві фігури називаються Рівними, якщо вони переводяться рухом одна в одну. Теорема. Рівні трикутники (означення дивись у розділі “Геометрія.”) є рівними фігурами, тобто суміщаються рухом....
6. Співнаправленість півпрямих Геометрія Рух Співнаправленість півпрямих Дві півпрямі називаються Однаково напрямленими або Співнапрямленими, якщо вони суміщаються паралельним перенесенням (рисунок 1). Теорема. Якщо півпрямі а і b однаково напрямлені й півпрямі b і c однаково напрямлені, то півпрямі а і c також однаково напрямлені. Дві півпрямі називаються Протилежно напрямленими, якщо кожна з них одна­ково напрямлена з півпрямою, допов­няльною […]...
7. Переміщення та його властивості. Рівні фігури УРОК № 33 Тема. Переміщення та його властивості. Рівні фігури Мета уроку: формування поняття переміщення та рівних фігур; вивчення властивостей переміщення. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур”. Рухи” [13]. Вимоги до рівня підготовки учнів: описують рівність фігур; будують фігури, у які переходять дані фігури при переміщеннях; формулюють властивості переміщення; застосовують вивчені означення […]...
8. Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
9. Подібність фігур Геометрія Подібність фігур Перетворення фігури F у фігуру називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів. Якщо відстані змінюються у k разів, то k називається Коефіцієнтом подібності. Якщо , перетворення подібності є рухом. Нехай F – дана фігура й О – фіксована точка. Через довільну […]...
10. Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
11. Гомотетія і перетворення подібності 480. ΔABC і ΔA1B1С1 гомотетичні з центром Р, R = 2. 481. Тетраедр DA1B1С1 гомотетичний тетраедру DABC відносно т. D, R = 0,5. 482. Р і A симетричні відносно В. Тетраедр A1B1C1D1 гомотетичний тетраедру ABCD відносно т. Р із коефіцієнтом R = -1. 483. В результаті гомотетії відносно т. А т. О – центроїд грані […]...
12. Теорема Фалеса Геометрія Чотирикутники Теорема Фалеса Теорема 1 (Фалеса). Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на другій його стороні. На рисунку ; ; . Зверніть увагу: . Теорема має місце не тільки для сторін кута, а й для довільних прямих. Теорема 2 (про […]...
13. Властивості паралельних площин Геометрія Стереометрія Властивості паралельних площин Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка […]...
14. Симетрія відносно прямої Геометрія Рух Симетрія відносно прямої Нехай а – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр AX на пряму а. На продовженні цього перпендикуляра за точку А відкладемо відрізок . Точка називається Симетричною точці X відносно прямої А. Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно прямої а. Очевидно, […]...
15. Паралельність прямих і площини Геометрія Стереометрія Паралельність прямих і площини Дві прямі в просторі називаються Паралельними, якщо вони лежать в одній площині й не перетинаються. Прямі, які не лежать в одній площині, називаються Мимобіж­ними. Зверніть увагу: “не лежать в одній площині” і “лежать у різних площинах” – це різні твердження. Наприклад, паралельні прямі a і b лежать у різних […]...
16. Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
17. Ознака паралельності прямих Геометрія Стереометрія Ознака паралельності прямих Теорема. Дві прямі, паралельні третій прямій, паралельні між собою. Із цієї теореми випливає, що середини сторін просторового чотирикутника (див. рисунок) є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині). Зверніть увагу: якщо ABCD – просторовий чотирикутник, то його діагоналі AC і BD – мимобіжні прямі....
18. Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
19. Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібно­сті випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...
20. Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...
21. Властивості паралельних площин Урок 18 Тема. Властивості паралельних площин Мета уроку: формування знань учнів про властивості паралельних площин. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування задачі № 24, у цей час клас пише математичний диктант. 2. Математичний диктант. Дано зображення куба: варіант 1 – рис. 64, варіант 2 – рис. 65. […]...
22. Паралельні прямі. Властивості паралельних прямих Урок № 110 Тема. Паралельні прямі. Властивості паралельних прямих Мета: закріпити знання учнів про властивості паралельних прямих; відпрацювати навички розв’язування задач, що передбачають застосування набутих з теми знань; продовжувати роботу з повторення вивченого у 6 класі матеріалу. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Математичний диктант […]...
23. Паралельне перенесення та його властивості Геометрія Рух Паралельне перенесення та його властивості Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b – одні й ті самі для всіх точок, називається Паралельним перенесенням. Теорема. Паралельне перенесення є рухом. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе) (див. рисунок). Існування […]...
24. Подібність фігур. Площі подібних фігур УРОК № 39 Тема. Подібність фігур. Площі подібних фігур Мета уроку: формування поняття подібності фігур; вивчення теореми про площі подібних фігур; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують подібність фігур; наводять приклади подібних фігур; формулюють теорему […]...
25. Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...
26. ІНДЕКС ПОДІБНОСТІ Екологія – охорона природи ІНДЕКС ПОДІБНОСТІ – число, яке застосовують для порівняння подібності або відмінності послідовних проб, узятих вздовж певних градієнтів зовн. середовища....
27. Симетрія відносно точки УРОК № 34 Тема. Симетрія відносно точки Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані […]...
28. Властивості паралельних прямих Урок № 8 Тема. Властивості паралельних прямих Мета: домогтися засвоєння учнями змісту таких понять: “теорема”, “доведення теореми”, “умова і висновок теореми”, а також алгоритму доведення методом від супротивного; використовуючи метод доведення “від супротивного”, довести терему про дві прямі, паралельні третій. Сформувати вміння: – відтворювати означення основних понять уроку; – застосовувати названі поняття під час розв’язування […]...
29. Перетворення простору 1. 1) Вектор паралельного перенесення, що переводить відрізок ОА в СВ: Вектор, що переводить відрізок ОС в АВ: 2) Вектор, що переводить ОС в АВ: Вектор, що переводить О А в СВ: 3) Вектор, що переводить ОС в АВ: Вектор, що переводить ОА в СВ: 4) Вектор, що переводить ОС в АВ: Вектор, що переводить […]...
30. Застосування подібності: властивість бісектриси трикутника Урок № 37 Тема. Застосування подібності: властивість бісектриси трикутника Мета: домогтися засвоєння учнями змісту теореми, що виражає властивість бісектриси трикутника та її доведення. Формувати вміння: – відтворювати зміст вивченої теореми; – за готовими рисунками із зображенням трикутника та його бісектриси знаходити пропорційні відрізки; – виконувати записи відповідно до формулювання теореми та умови задачі; – застосовувати […]...