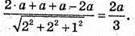Властивості призми
1.
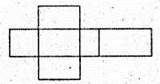
2.
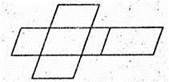
3.
Ні, не можна.
4.
Бічні ребра перпендикулярні до основи. Усі бічні грані – прямокутники.
Бічне ребро є висотою призми. Площа бічної поверхні – добуток периметра
Основи на довжину бічного ребра.
5.
Так, може. Див. мал. до № 2.
6.
1) Основа правильної призми – правильний багатокутник,
Усі бічні грані – рівні прямокутники.
2) Усі грані куба є рівними квадратами.
7.
Так, можна. Бічне ребро прямої призми перпендикулярне до основи,
А
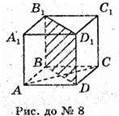
8.
В основі призми лежить квадрат. АС + BD
(оскільки діагоналі квадрата перетинаються під прямим кутом).
АС + DD1 (оскільки бічне ребро перпендикулярне основі,
А отже перпендикулярне будь-якій прямій в цій площині).
Маємо АС + BD. АС + DD1прямі BD + DD1 — перетинаються,
А отже АС перпендикулярна площині BB1DD1.
9.
Розгортка бічної поверхні похилого паралелепіпеда є паралелограмом.
Див. мал. до № 2.
10.
Якщо сума площ протилежних бічних граней прямої чотирикутної призми рівні між собою, то
11.
Оскільки у прямої призми бічні ребра перпендикулярні до основи, то бічні ребра перпендикулярні і до будь-якої прямої, що належить площині основи, в тому числі і прямим, які містять діагоналі основи.
12.
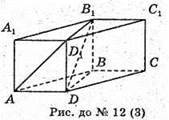
1) AD = 3 см; AA1= 4 см; DC = 6 см.
Розглянемо трикутник ACC1- прямокутний (∠ACC1= 90º).
За теоремою Піфагора: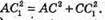 
CC1 = AA1- оскільки бічні ребра рівні).
З трикутника ADC – прямокутного (∠ADC = 90º) знайдемо АС.
За теоремою Піфагора: АС2 = AD2 + DC2·, АС2 = 32 + 62 = 9 + 36 = 45.
Тоді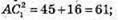 
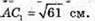
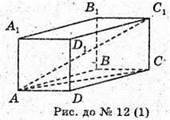
2) AD = 3 см; DC = 4 см; ∠C1AC = 30°.
Розглянемо трикутник АСС – прямокутний (∠ACC1 = 90°).
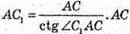знайдемо з трикутника ACD-прямокутного (∠ADC = 90°).
За теоремою Піфагора: АС2 = AD2 + DC2 ; АС2 = 32 + 42 = 25; АС = 5.
Тоді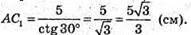 
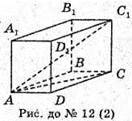
3) AD= 2 см; DС = 3 см; ∠D1AD = 60°.
Розглянемо трикутник ADD1- прямокутний (∠ADD1 = 90°).
DD1= AD × tg∠D1AD;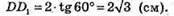 
Розглянемо трикутник BAD – прямокутний (∠BAD = 90°).
За теоремою Піфагора: BD2= АВ2 + AD2.
AB = DC (оскільки ABCD – прямокутник).
BD2 = З2 + 22 = 9 + 4 = 13;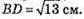 
Розглянемо трикутник B1BD прямокутний (∠B1BD = 90º).
За теоремою Піфагора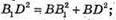 
BВ1 = DD1(оскільки бічні ребра прямокутного паралелепіпеда рівні).
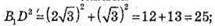B1D = 5 см.
13.
Знайдемо площу бічної основи прямої чотирикутної призми.
S = Росн × h. Висота прямої призми дорівнює довжині бічного ребра.
S = (2 + 3 + 2,5 + 4,5) × 5 = 60 (см2).
14.
Знайдемо площу повної поверхні призми. Sповн = Sбічн + 2Sосн
В основі призми лежить ромб зі стороною 5 см і гострим кутом 30°.
Його площа S = а2 × sin α;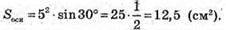 
Знайдемо площу бічної поверхні. Sбічн = Росн × h.
Висота дорівнює довжині бічного ребра, оскільки призма пряма.
Sбічн = 4 × 5 × 10 = 200 (см2).
Тоді площа повної поверхні: Sповн = 200 + 2 × 12,5 = 225 (см2).
15.
Знайдемо площу повної поверхні правильної чотирикутної призми.
Sповн = Sбічн + 2 Sосн
В основі лежить квадрат зі стороною 10 дм, його площа:
Sосн = 102 = 100 (дм2). Знайдемо площу бічної поверхні: Sбічн = Росн × h.
Висота дорівнює довжині бічного ребра, оскільки призма правильна.
Sбічн = 4 × 10 × 8 = 320 (дм2).
Тоді площа повної поверхні: Sоcн = 320 + 2 × 100 = 520 (дм2).
16.
Розглянемо призму, в основі якої лежить n-кутник.
Ця призма має 2n тригранних кутів (n при нижній основі, n – при верхній),
А це число парне.
17.
Призма має n граней. Дві з них є основами. Отже бічних граней n – 2,
А в основі призми лежить n-2-кутник.
18.
Припустимо, що з вершини виходить 4 ребра, це означає, що призма має два бічних ребра, які не співпадають, тобто не паралельні, а це суперечить означенню призми. Значить, з однієї вершини може виходити лише три ребра.
19.
Нехай в основі призми лежить n-кутник.
Тоді кількість його ребер Зn, тобто кратне 3. 14 не кратне 3.
Отже не існує призми, яка має 14 ребер.
20.
Обернене твердження. Якщо бічні грані призми рівні прямокутники, то це правильна шестикутна призма.
Це твердження хибне. Розглянемо пряму призму, в основі якої лежить правильний трикутник, бічні грані цієї призми будуть рівними прямокутниками, але це не означає, що в її основі лежить шестикутник.
21.
1) Похила призма, основою якої є правильний багатокутник із непарною кількістю сторін може мати одну грань у формі прямокутника,
2) Похила призма, основою якої є правильний багатокутник із парною кількістю сторін може мати дві грані у формі прямокутника.
22.
Доведемо, що утворена фігура буде квадратом.
За умовами АК + DM = AD; МС + ВК = ВС.
Складемо рівності АК + DM + МС + ВК =AD + ВС; АВ + DC=AD + ВС;
АВ = DC; AD = ВС; 2АВ = 2AD; AB =AD.
∠A = ∠B = ∠C = ∠D = 90° (оскільки трапеція прямокутна). Отже ABCD – квадрат. Бічні ребра перпендикулярні основі. Утворене тіло буде правильною чотирикутною призмою.
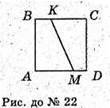
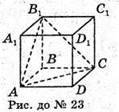
23.
AВ1С – пеперіз, що проходить через три несуміжні вершини.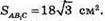 
ABCDA1B1C1D1 – куб. Всі його грані рівні, а отже рівні і діагоналі граней.
Трикутник AB1C – правильний.
Площа правильного трикутника: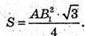 
Звідси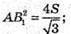 
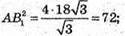
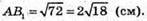
Розглянемо трикутник ADC – прямокутний, рівнобедрений (∠ADC = 90°).
∠CAD = 45°; AD = АС × cos∠CAD; AC = АВ1;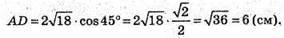 
24.
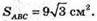Трикутник ABC – правильний, його площа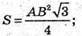 
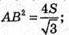
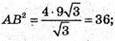АВ = 6 см.
Оскільки висота в три рази більше, АА1 = 18 см. Тоді площа бічної поверхні
Sбічн = Росн × h; h = АА1. Sбічн = 3 × 6 × 18 = 324 (см2).
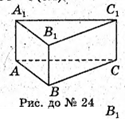
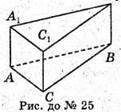
25.
Трикутник АСВ – прямокутний рівнобедрений (∠ACB = 90°).
Його площа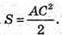 
Звідси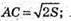 
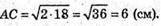
З трикутника АСВ за теоремою Піфагора АВ2 = АС2 + ВС2;
АС = ВС. АВ2 = 62 + 62 = 72;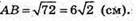 
Площа бічної поверхні Sбічн = (AB + BC + AC) × AA1;
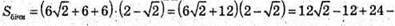
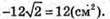
26.
Трикутник ABC – рівнобедрений, АС СВ = 5 см, АВ = 8 см,
СК – висота трикутника ABC, проведена до основи.
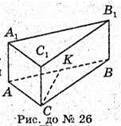
Оскільки ΔАВС – рівнобедрений, то СК буде також і медіаною,
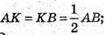КВ = 4 см. АВ + СК (оскільки СК – висота).
Розглянемо трикутник СКВ – прямокутний (∠CKB = 90). З теореми Піфагора
Маємо: СК2 = ВС2 – КВ2; СК2 = 52 – 42 = 9. СК = 3 см, АА1 = СК = З см (за умовами).
Тоді площа бічної поверхні Sбічн = (АВ + ВС + АС) × АА1;
Sбічн = (8 + 5 + 3) × 3 = 54 (см2).
27.
1 випадок: АВ =10 см, AD = 26 см.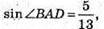 
∠B1DB = 45º,
Розглянемо трикутник ABD. За теоремою косинусів:
BD2 = AB2+AD2- 2AB × AD cos∠BAD.
З основної тригонометричної тотожності: cos2∠BAD =1 – sin2∠BAD;
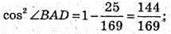
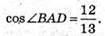
Тоді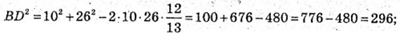 
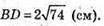
Обчислимо площу бічної поверхні:
Sбічн = 2(АB + AD) × ВВ1, ВВ1 знайдемо з трикутника B1ВD –
Прямокутного (∠B1BD = 90°), рівнобедреного (ΒD = ВВ1).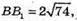 
Тоді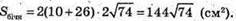 
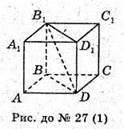
2 випадок: АВ = 10 см, AD = 26 см;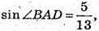 
∠C1AC = 45°.
Розглянемо трикутник ADC. cos∠ADC = – cos∠BAD.
За теоремою косинусів: АС2 = AD2 + DC2- 2AD × DC × cos∠ADC;
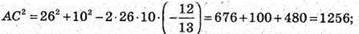
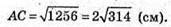
ΔACC1- прямокутний, рівнобедрений (∠ACC1 = 90°; АС = СС1).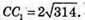 
Тоді площа бічної поверхні Sбічн = 2(АВ + ВС) × СС1
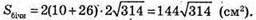
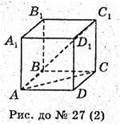
28.
Нехай довжина ребра куба дорівнює а, КС1 = КА.
Розглянемо трикутник KD1C1 – прямокутний.
За теоремою Піфагора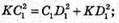 
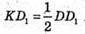
(К – середина ребра DD1). Тоді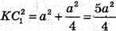 
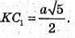
Знайдемо довжину діагоналей куба AC1
З трикутника ADC – прямокутного рівнобедреного
(∠ADC = 90°).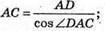 
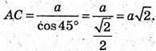
З трикутника АСС1 – прямокутного (∠ACC1 = 90°)
За теоремою Піфагорa: .
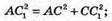
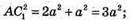
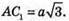
Знайдемо площу трикутника AКC1 за формулою Герона.
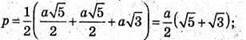
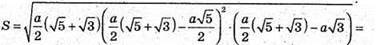
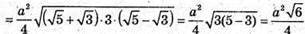
За умовами: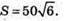 
Отримуємо рівняння: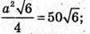 
а2 = 200;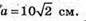 
29.
ABCDA1B1C1D1 – прямокутний паралелепіпед.
АВ = 5 см, AD = 3 см.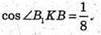 
Розглянемо трикутник ADC – прямокутник (∠ZADC = 90°).
За теоремою Піфагора: АС2 = ΑD2 + DC2; АС2 = 52 + З2 = 25 + 9 = 34:
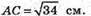
АС = BD, К – точка перетину діагоналей основи.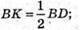 
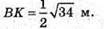
Розглянемо трикутник В1ВК – прямокутний (∠B1BK = 90°).
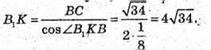
Розглянемо трикутник AB1C. Його площа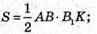 
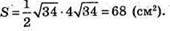
30.
KLCB1- утворений переріз. KLCB1 – трапеція (KL? В1С),
B1K = LC1 трапеція рівнобічна.
Розглянемо трикутник B1A1C – прямокутний (∠B1A1K1 = 90°).
За теоремою Піфагора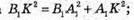 
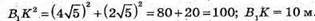
З трикутника В1ВС – прямокутного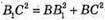 
– за теоремою Піфагора.
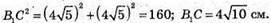
З трикутника KD1L – прямокутного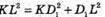 
– за теоремою Піфагора.
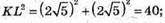
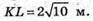
Знайдемо висоту трапеції КМ. Оскільки трапеція рівнобічна:
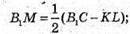
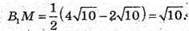
Розглянемо трикутник В1KМ – прямокутний (∠B1KМ = 90°).
З теореми Піфагора: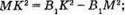 
МК2 = 100 – 10 = 90;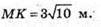 
Обчислимо площу перерізу.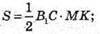 
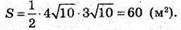
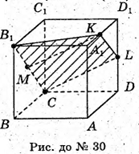
31.
AD1C – утворений переріз. ∠D1KD = 60º; АВ = 4 см.
Розглянемо трикутник D1DK – прямокутний (∠D1DK = 90°).
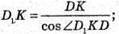
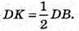
З трикутника DAB – прямокутного за теоремою Піфагора DB2 = AD2+ АВ2;
DB2 = 16 +1 = 32;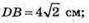 
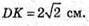
Тоді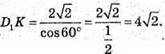 
AC = DB.
Площа трикутника AD1C: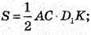 
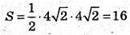
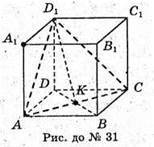
32.
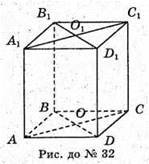
ABCD – ромб, SAA1C1C =4 см2; SBB1D1D = 3 см2.
Позначимо АС = d1, BD = d2, АА1 = h.
Площа діагональних перерізів d1h = 3, d2h = 4.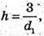 
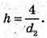
Отримуємо рівняння: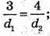 
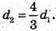
Розглянемо трикутник AOD – прямокутний (∠AOD = 90°).
AD2 = AO2 + OD2 – за теоремою Піфагора.
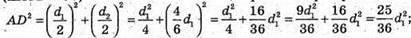
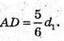
Площа бічної поверхні Sбічн = 4AD • АА1;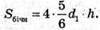 
Оскільки d1h = 3, маємо: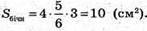 
33.
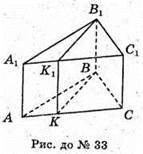
АВСА1В1С1 – правильна трикутна призма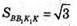
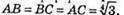
Розглянемо трикутник ABC – правильний. ВК – його висота.
Трикутник ΑKΒ- прямокутний, ∠AВK = 30°, оскільки ВК є також і бісектрисою,
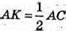, оскільки ВК – медіана. ВК = АК × ctg∠ΑΒΚ;
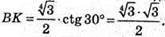
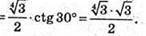
Знайдемо площу перерізу. SВВ1К1К = ВК × ВВ1;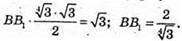 
Знайдемо площу бічної поверхні: Sбічн = ЗАС × ВВ1;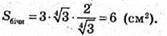 
Знайдемо площу основи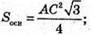 
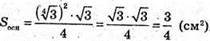
Тоді площа повної поверхні: Sповн = Sбічн + 2Sосн
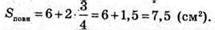
35.
Введемо прямокутну систему координат із початком у точці А
І спрямуємо вісь Ох вздовж ребра АО, Оу – вздовж ΑΒ, Οz – вздовж АА1.
Тоді координати точок (оскільки ребро куба дорівнює a) D(a; 0; 0), В(0; а; 0),
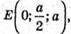
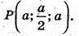
Запишемо рівняння площини, що проходить через точки В, D I E.
Рівняння площини має вигляд: nх + mу + рz + 1 = 0.
Знайдемо коефіцієнти n, m і р.
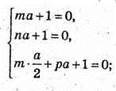
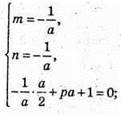
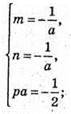
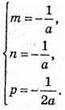
Тоді рівняння площини:
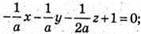
2х + 2у + z – 2а = 0.
Знайдемо відстань від точки Р до площини.
(1 votes, average: 5.00 out of 5)
Loading...