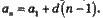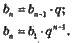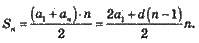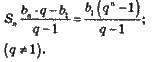Властивості прогресій – ПРОГРЕСІЇ
Формули й таблиці
МАТЕМАТИКА
ПРОГРЕСІЇ
Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел:
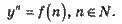
Арифметична прогресія | Геометрична прогресія |
Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. | Геометричною прогресією |
Числа, що становлять прогресію, називаються її членами. Число, яке потрібно додати до попереднього члена, щоб одержати наступний, називається різницею прогресії. | У геометричній послідовності частка від ділення наступного члена на попередній називається знаменником прогресії q(q ≠ Q). |
Загальний член арифметичної прогресії аn дорівнює першому її члену a1, складеному з добутком різниці прогресії d на число
| Будь-який член геометричної прогресії bn, знаменник якої q, визначається:
|
Сума n членів арифметичної прогресії дорівнює половині добутку суми крайніх членів на кількість членів:
| Сума перших n членів геометричної прогресії
Якщо lql < 1 , тоді q
|
Властивості прогресій
Арифметична прогресія
– кожен середній член арифметичної прогресії дорівнює середньому арифметичному рівновіддалених від нього членів:
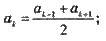
– у кінцевій арифметичній прогресії суми двох членів, рівновіддалених від її кінців, рівні між собою й дорівнюють сумі крайніх членів:
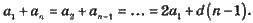
Геометрична прогресія
– квадрат кожного середнього члена геометричної прогресії дорівнює добутку рівновіддалених від нього членів:
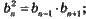
– у кінцевій геометричній прогресії добутки двох членів, рівновіддалених від її кінців, рівні між собою й дорівнюють добутку крайніх членів:
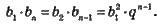
Related posts:
- Числові послідовності УРОК № 65 Тема. Числові послідовності Тестові завдання 1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3. А) 3; б) 17; в) 5; г) інша відповідь. 2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3. А) 1536; б) 18; в) 21; г) інша відповідь. 3. Знайдіть суму перших […]...
- Сума перших n членів геометричної прогресії УРОК № 57 Тема. Сума перших n членів геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед числових послідовностей, відшукувати знаменник геометричної прогресії, перші члени геометричної прогресії, а […]...
- Арифметична прогресія. Формула n-го члена арифметичної прогресії УРОК № 51 Тема. Арифметична прогресія. Формула n – го члена арифметичної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять арифметичної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена арифметичної прогресії. Закріпити вміння: вирізняти арифметичну прогресію серед числових послідовностей, відшукувати різницю арифметичної прогресії, перші члени […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- Сума перших n членів арифметичної прогресії УРОК № 53 Тема. Сума перших n членів арифметичної прогресії Мета уроку: закріпити знання учнів про формули обчислення суми перших n членів арифметичної прогресії, а також про її означення та властивості, вивчені на попередніх уроках; сформувати уявлення про спосіб розв’язування задач на відшукання суми послідовних членів арифметичної прогресії з n-го по т-й включно (n < […]...
- Геометрична прогресія Математика – Алгебра Послідовності Геометрична прогресія Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії. Формула n-го члена геометричної прогресії: . Теорема. Послідовність тоді й тільки тоді є геометричною […]...
- Геометрична прогресія. Формула n-го члена геометричної прогресії УРОК № 55 Тема. Геометрична прогресія. Формула n-го члена геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед інших числових послідовностей, відшукувати знаменник геометричної прогресії, перші кілька членів […]...
- Геометрична прогресія УРОК № 54 Тема. Геометрична прогресія Мета уроку: домогтися засвоєння учнями: означення геометричної прогресії, відповідної термінології (знаменник геометричної прогресії), її рекурентної формули та основних властивостей геометричної прогресії (включаючи характеристичну властивість). Виробити вміння: відтворювати зміст вивчених понять, а також використовувати їх для розв’язування задач, що передбачають виділення геометричної прогресії серед інших числових послідовностей, використання рекурентної формули […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Відношення та пропорції Математика – Алгебра Множення і ділення звичайних дробів Відношення та пропорції Відношенням двох чисел називається частка цих чисел. Відношення показує, у скільки разів одне число більше від другого або яку частину становить одне число від другого. Щоб знайти відношення двох величин, вони мають бути виміряні однією й тією ж одиницею вимірювання. Наприклад, відношення 3 км […]...
- ПРОПОРЦІЯ ТА її ВЛАСТИВОСТІ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ §13. ПРОПОРЦІЯ ТА її ВЛАСТИВОСТІ Ви знаете, що два вирази, які мають рівні значення, можна прирівняти. Наприклад, можна прирівняти відношення 1,2 : 0,3 і 16 : 4, оскільки їх значення дорівнюють 4. Отже, можна записати рівність: Такі рівності мають спеціальну назву – пропорція. Пропорцією називається рівність двох відношень. Зверніть увагу: […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Основні властивості кубічного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості кубічного кореня Для будь-яких дійсних чисел a й b: 1) а = ()3; 2) = а; 3) = ; 4) якщо b ≠ 0, то ; 5) = тільки тоді, коли а = b; 6) < тільки тоді, коли а < b; 7) < тільки тоді, […]...
- Властивості множення раціональних чисел Урок № 8 3 Тема. Властивості множення раціональних чисел Мета: повторити відомі учням властивості множення натуральних та дробових чисел, поширити їх на множення раціональних чисел і вдосконалити вміння виконувати множення раціональних чисел (використовуючи переставну, сполучну та властивості 0 та 1 при множенні) Тип уроку: систематизація та узагальнення знань, умінь, навичок Хід уроку I. Перевірка домашнього […]...
- Властивості модуля – Модуль і його властивості Математика – Алгебра Модуль і його властивості Модуль числа – це відстань від 0 до точки, що відповідає цьому числу на координатній прямій, виміряна в одиничних відрізках. Отже, для всіх значень a. Властивості модуля 1. . 2. Якщо , то . 3. Якщо , то 4. Модуль суми скінченного числа дійсних чисел не перевищує суми […]...
- Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...
- Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Переставна і сполучна властивості множення. Коефіцієнт буквеного виразу Розділ 4 Раціональні числа і дії мідними §44. Переставна і сполучна властивості множення. Коефіцієнт буквеного виразу Для множення раціональних чисел, як і для множення додатних чисел, справджуються переставна і сполучна властивості. Переставна властивість множення. – Для будь-яких раціональних чисел а і b виконується рівність ab = ba. Перевіримо цю властивість на прикладах. Приклад 1. -3 […]...
- ВІДНОШЕННЯ ТА ЙОГО ВЛАСТИВОСТІ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ У розділі дізнаєтесь: Ü про відношення та його властивості; Ü що таке пропорція; Ü які є пропорційні залежності величин; Ü як поділити число в даному відношенні; Ü що таке масштаб; Ü про коло, круг, круговий сектор та просторові фігури обертання; Ü які є види діаграм та як будувати діаграми; Ü […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- Рівняння та їх властивості. Розв’язування задач за допомогою рівнянь Урок № 106 Тема. Рівняння та їх властивості. Розв’язування Задач за допомогою рівнянь Мета: діагностика рівня засвоєння знань та вмінь, передбачених програмою з названої теми. Тип уроку: перевірка і корекція знань, умінь та навичок. Хід уроку I. Організаційний момент (Перевіряємо готовність до уроку, збираємо робочі зошити на перевірку; оголошуємо умову та вимоги до виконання завдань […]...
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ Розділ 5 ВИРАЗИ І РІВНЯННЯ § 31. РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ Ви вже знаете, що таке рівняння, корінь рівняння. Пригадаємо основні формулювання. Запам’ятайте Рівнянням називається рівність, що містить невідоме, значення якого треба знайти. Невідоме число в рівнянні позначають буквою х, або у, або z тощо. Наприклад, запис 4х + 7 = 15 є рівнянням, де […]...
- ДОВЕДЕННЯ ТОТОЖНОСТЕЙ Цілі: – навчальна: удосконалити вміння учнів доводити тотожності; – розвивальна: формувати вміння міркувати за аналогією; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати упевненість у власних силах, уміння самоорганізовуватися, спостережливість; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ […]...
- ПЛОЩА ПРЯМОКУТНИКА ПЛОЩА ПЛОЩА ПРЯМОКУТНИКА 627. Знайди площі трьох фігур. Перевір обчисленнями. Порівняй. 628. Прямокутник ABCD поділений на квадратні сантиметри. Полічи, скільки квадратних сантиметрів у прямокутнику. Знайди число квадратних сантиметрів: 1) додаванням: А) 5 см2 + 5 см2 + 5 см2 =15 см2. (в одному ряду 5 одиничних квадратів, а рядів три). Б) 3 см2 + 3 […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Сполучна і розподільна властивості множення Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 17. Сполучна і розподільна властивості множення Нарисуємо на аркуші в клітинку прямокутник із сторонами 5 см і 3 см. Розіб’ємо його на квадрати зі стороною 1 см (рис. 142). Підрахуємо кількість клітинок зошита, що містяться в прямокутнику. Це можна зробити, […]...
- ВЛАСТИВОСТІ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ ВЛАСТИВОСТІ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ A + b = b + a A + (b + c) = (a + b) + c = a + b + c Додавання числа до суми Додавання суми до числа Віднімання числа від суми Віднімання суми від числа (a – b) + c = (a + c) – […]...