Властивості степеня з натуральним показником. Добуток степенів з однаковою основою
Урок № 21
Тема. Властивості степеня з натуральним показником. Добуток степенів з однаковою основою
Мета: домогтися свідомого розуміння учнями властивості добутку степенів з однією основою та сформувати вміння перетворювати числові та буквені вирази з використанням цієї властивості.
Тип уроку: засвоєння знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
(Зібрати зошити)
II. Актуалізація, опорних знань
Виконання усних вправ
1. Які з виразів с степенем з натуральним показником?
23; 2-5; 2 – (-5);
Для степенів із натуральним показником назвіть основу та показник. Як записати ці степені у вигляді добутку? Обчисліть значення степеня.
2. Не обчислюючи значення виразів, порівняйте їх з нулем:
(-5)13; (-5)12; -512; (х – 1)12; (х – 1)13 ; -(х – 1)12.
Які міркування ви використали?
3. Знайдіть квадрати, куби, 4 та 5-ті степені чисел 2 і 3, заповніть таблицю:
N | 2 | 3 | 4 | 5 |
2n | ||||
3n |
III. Робота з випереджальним домашнім завданням
Завдання. Доведіть, що добуток а3 і а2 дорівнює а5.
@
Додаток
Алгоритм доведення
1. Установи і сформулюй проблему, яку треба довести.
2. Дай означення поняттям, за допомогою яких буде здійснюватись доведення.
3. Добери достатньо грунтовні аргументи.
4. Визнач спосіб і логіку доведення.
5. Зроби висновок.
Аргументи (підстави) – судження, істинність яких перевірена й доведена практикою. Головною характеристикою є істинність, тобто відповідність дійсності.
@ Зрозуміло, що виконання цієї роботи буде легким для учнів, бо у випереджальному завданні є натяк на ті дії, що передбачені алгоритмом. Тому по виконанні цього завдання не виникає сумніву в тому, що a3 – a2 = a5.
Порівняйте ліву й праву частину рівності. Сформулюйте гіпотезу.
IV. Засвоєння знань. Проблемна ситуація
Завдання 1. Довести, що а5 – а8 = а13; а – а12 = а13.
Завдання 2. Довести, що а13 – а27 = а40.
Завдання 3. Як подати у вигляді степеня добуток а135 – а247 ?
1) Усвідомлюємо суть усіх завдань: за аналогією з розв’язаними раніше намагаємось довести, що добуток двох степенів з однією основою є степенем з тією самою основою, а показник – сума показників множників.
2) Обираємо спосіб доведення (за аналогією з випереджальним домашнім завданням), але, щоб “узагальнити” запис, замінюємо числові показники буквами й формулюємо твердження, що є основою для розв’язування завдань 1-3.
Доведіть, що аn – аm = аn+m, якщо а – будь-яке число; m і n – натуральні числа.
Доведіть (за алгоритмом та аналогією з доведеного рівністю а3 – а2 = а5) може провести вчитель або запропонувати виконати учням.
Запис у зошитах може мати такий вигляд:
Конспект 7 |
Добуток степенів з однією основою |
1. Якщо а – будь-яке число; m, n – натуральні числа, то аn – аm = аn+m. |
Доведення |
|
2. Приклади: |
А5 – а8= а5+8 = а13; а13 – а27 = а40; а135 – а247 = а382. |
Зауваження, а – а11 = а12, бо а = а1. (Така домовленість) |
V. Застосування знань, умінь та навичок
@ Завдання на закріплення розуміння учнями основної властивості степеня (аm – аn = аm+n) передбачають:
1) закріплення термінології;
2) засвоєння умінь перетворювати добуток степенів з однаковою основою у степінь;
3) засвоєння вмінь перетворювати степінь на добуток степенів з однією основою;
4) повторення вивчених властивостей степенів з парними й непарними показниками.
Тому система завдань, що допоможе вчителю та учням досягти визначеної мети, може бути такою:
Виконання усних вправ
1. Який з добутків виразів можна подати у вигляді степеня з використанням основної властивості степеня:
А3 – а5; а3 – b5; а3 – а2 – а7; (а + b)2(а + b)3; 3m -3n; 32 – 92; m3 – n3?
Чому?
2. Подайте вираз у вигляді степеня:
Х5 – х7; 5 – 52; а – а3; у4 – у6 – у; 102 -10 – 103; с – с – с3; z – z5; 74 – 49; (-6) – (-6)3 – (-6); a2n – an.
3. Який вираз треба поставити замість *, щоб рівність а2 – а* = а6 була правильною? Чому?
Виконання письмових вправ
1. Подайте у вигляді степеня добуток:
1) m5 – m3;
2) х – х6;
3) а4 – а4;
4) 54 – 54;
5) у3 – у8 – у5;
6) с7 – с – с2;
7) (m – n)8(m – n)3;
8) (u + v)3-(u + v);
9) (a – b)(a – b)(a – b)2;
10) х2п – х2n-2;
11) хn – х5.
2. Замініть * на степінь так, щоб рівність стала правильною:
1) a8 – * = a13;
2) a11 – * – a = a16.
3. Знайдіть значення змінної, при якому буде правильною рівність:
1) 45 – 43 = 45+х;
2) 23 – 22 = 21+x;
3) 2n – 25 = 27;
4) 34 – 3n = 37;
5) 75 – 7x = 72х-1;
6) 75 – 7x = 715-2х.
4*. Спростіть вираз:
1) а10 – а12 -(-а5);
2) х – (-х) – (-х6);
3) уn – у8 – у2;
4) bn – bn – b3.
5*. Подайте у вигляді добутку двох множників, один з яких а5, такі вирази:
1) a10; 2) a6; 3) – a40.
6*. Подайте у вигляді степеня вираз: 1) 25 – 8; 2) 4 – 8; 3) 7n – 49; 4) 27 – 3n.
@ Перед виконанням порівняємо умови вправи № 6 із розв’язаними попередньо і знайдемо відмінність (множники якщо і є степенями, то з різними основами), отже, спираючись на № 3 поданих вправ, замінюємо множник(и) степенями з однаковими основами й використовуємо основну властивість степеня.
7. Логічна вправа. Знайдіть пропущені записи:
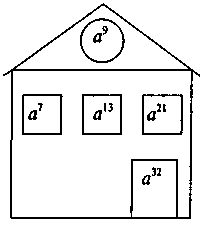
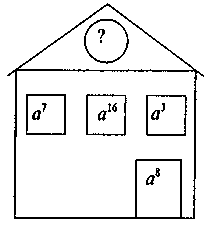
V. Підсумки уроку. Рефлексія
На окремих картках записано етапи використання основної властивості степеня для спрощення виразів; картки пропонуються учням в хаотичному порядку, наприклад:
1) показники додати | 2) перевірити, чи рівні основи | 3) основу не змінюємо | 4) якщо показник не записано, вважаємо його за 1 |
Учням пропонується встановити правильний порядок дій під час пошуку відповідей на запитання:
Як знайти добуток степенів з однією основою?
VI. Домашнє завдання
№ 1. Подайте у вигляді степеня добуток:
1) а9 – а2; 2) а – а7; 3) b3 – b3; 4) 711 – 73; 5) m4 – m5 – mn; 6) c19 – с – сn; 7) (a+b)(a+b)7; 8) n9 – n4 – nk+1 – n.
№ 2. Замініть * степенем з основою а, щоб утворилась правильна рівність:
1) а11 – * = a13; 2) a3 – * – a = a25.
№ 3. Подайте у вигляді степеня: 1) 58 – 25; 2) 312 – 27; 3) 29 – 16.
№ 4. Випереджальне домашнє завдання. Які правильні рівності можна записати з того, що a – b = c?
(Як знайти множник а; множник b?)
Які рівності, відповідно, випливають з того, що а3 – а2 = а5
(за умови, що а?0)?
Як прочитати ці рівності словами?
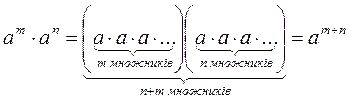 .
.