Головна ⇒ 📌ГДЗ з математики ⇒ Вправи 425-474

Вправи 425-474

425.

Вправи 425 474

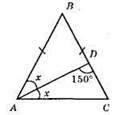
АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°.

Відповідь: 20°, 20°, 140°.

426.

Вправи 425 474

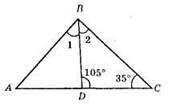
?DBC; ∠BDC = 105°; BD – бісектриса.

?DBC; ∠DBC = 180° – (105° + 35°) = 180° – 140° = 40°; ∠B = ∠1 + ∠2 = 40° + 40° = 80°; ∠A = 180° – (35° + 80°)= 180° – 115° = 65°.

Відповідь: 65°.

427. BD і AK – бісектриси;

∠A = 82°, ∠B = 38°.

∠1 = ∠2 = ∠A : 2 = 82° : 2 = 41°;

∠3 = ∠4 = ∠B = 38° :

2 = 19°.

Вправи 425 474

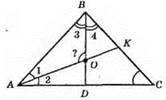
?AOB. ∠1 = 41°; ∠3 = 19°;

?AОВ = 180° – 41° – 19° = 180° – 60° = 120°.

Відповідь: ∠AOB = 120°.

428.

Вправи 425 474

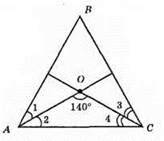
?ABC – рівнобедрений; AB = СВ; ∠AOC = 140°.

?АОС; ∠2 = ∠4 = (180° – 140°) : 2 = 20°;

∠A = ∠1 + ∠2; ∠C = ∠3 + ∠4; ∠A = ∠C = 40°;

∠B =180°- (40° + 40°) = 180° – 80° = 100°.

Відповідь: 100°.

429.

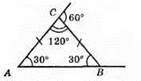
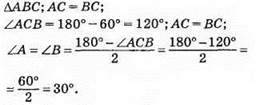
Вправи 425 474

Вправи 425 474

Відповідь: 30°, 30°, 120°.

430.

Вправи 425 474

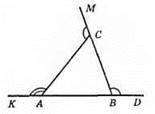
∠ACM : ∠KAC : ∠DBC = 3 : 4 : 5;

∠ACM = 3х; ∠KAC = 4х; ∠DBC = 5х;

3х + 4х + 5х = 360°; 12x = 360°; x = 360°: 12; x = 30°;

∠ACM = 3 x 30°

= 90°;

∠KAC = 4 х 30° = 120°;

∠DBC = 5 х 30° = 150°;

∠ACB = 180° – 90° = 90°;

∠CAB = 180° – 120° = 60°;

∠CBA = 180° – 150° = 30°.

Відповідь: 90°, 60°, 60°.

431.

Вправи 425 474

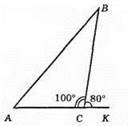
∠BCK = 80°; ∠BCA = 180° – 80° = 100°. ∠A + ∠B = 80°; ∠B + ∠C= 150°;

∠C = 150° – ∠C = 150° – 100° = 50°;

∠A = 80° – 50° = 30°.

Відповідь: 30°, 50°, 100°.

432.

Вправи 425 474

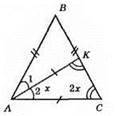
AK = AC, AB = ВС; ?АКС – рівнобедрений; ∠1 = ∠2; АК – бісектриса; ∠A = ∠C = ∠1 + ∠2.

У? АКС; ∠2 = x° ∠C = 2х; ∠K = 2х; х + 2х + 2х = 180°; 5х = 180°; x = 180° : 5; x = 36°; ∠A = ∠C = 2 х 36°; ∠B = 180° – (72° + 72°) = 180° – 144° = 36°.

Відповідь: 36°, 72°, 72°.

433.

Вправи 425 474

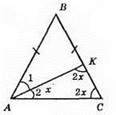
AB = ВС; АК – бісектриса кута A.

∠A = ∠C; ∠1 = ∠2; ∠K = ∠C; ∠A = ∠K = ∠C; ∠2 = x; ∠K = ∠C = 2х; х + 2х + 2х = 180°; 5х = 180°; x = 180°: 5; x = 36°.

∠C = ∠A = 2 x 36° = 72°;

∠B = 180° – (72° + 72°) = 36°.

Відповідь: 72°, 72°, 36°.

434.

Вправи 425 474

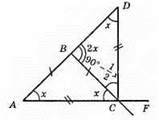
?ABC; AB = BC; ∠BCF – зовнішній кут? ABC при основі; ∠BCD = ∠FCD, CD – бісектриса зовнішнього кута. ?ABC – рівнобедрений, AB = BC, ∠A = ∠C = x, ∠CBD = 2x (зовнішній кут ДABC при вершині В).

?CAD – рівнобедрений; DC = АС; ∠A = ∠D = х; ∠BCF = 180° – х;

Вправи 425 474

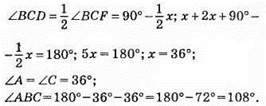
Відповідь: 36°, 36°, 108°.

435. Дивись малюнок до задачі 434.

?ABC – рівнобедрений, AB = ВС;

∠A = ∠C = х; ∠A = ∠D = х (за умовою); ∠CBD – зовнішній кут? ABC при вершині B. CBD = 2x;

Вправи 425 474

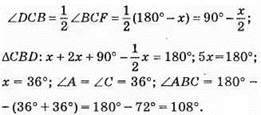
Відповідь: 36°, 36°, 108°.

436.

Вправи 425 474

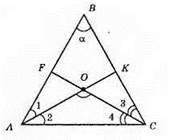
?АВС; АК – бісектриса ∠A, ∠1 = ∠2; CF – бісектриса ∠C; ∠3 = ∠4.

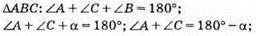
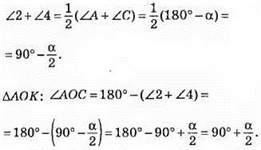
Вправи 425 474

Вправи 425 474

∠AOC – кут між бісектрисами? ABC; ∠AOC = 90° + α/2.

437.

Вправи 425 474

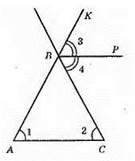
?ABC – рівнобедрений; AB = ВС; ∠A = ∠C; ∠KBC – зовнішній кут рівнобедреного трикутника при вершині; ВР – його бісектриса; ∠ABC = 180° – (∠A + ∠C); ∠KPC = ∠1 + ∠2, ∠1 = ∠2; ∠KPC = ∠3+ ∠4; ∠3 = ∠4, отже, ∠4 = ∠2 при прямих РВ і АС, ВС – січна. Отже, ВР || АС.

438. Якщо промінь, що проходить між сторонами зовнішнього кута при вершині рівнобедреного трикутника паралельний його основі, то цей промінь є бісектрисою цього зовнішнього кута.

Вправи 425 474

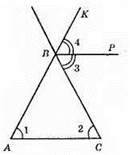
ВР – промінь, BP || АС; ∠2 = ∠3 – внутрішні різносторонні кути; ∠KBP = ∠1 + ∠2 (властивість зовнішнього кута трикутника). ∠KBP = ∠3 + ∠4; ∠1 + ∠2 = ∠3 + ∠4; ∠1 = ∠2 = ∠3, отже, ∠1 = ∠2 =∠3 = ∠4, ∠3 = ∠4. Промінь ВР – бісектриса кута.

439.

Вправи 425 474

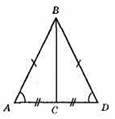
?ABC = ?DBC; AB = BD, АС = CD; ∠A = ∠D; ∠ACB = ∠DBC, а це суміжні кути; ∠ACB = ∠DCB = 90°; ?ABC і? DBC – прямокутні.

440.

Вправи 425 474

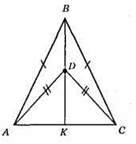
?ABC; AB = ВС. ?ADC; AD = DC. ?ABD = ?CBD за трьома сторонами; AB = ВС; AD = DC;BD – спільна сторона. З їхньої рівності: ∠ABD = ∠CBD. Отже, у? ABC ВК є бісектрисою, ?ABC – рівнобедрений, ВК є висотою. Отже, BK ⊥ AC (BD ⊥ AC).

441.

Вправи 425 474

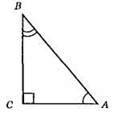
∠A + ∠B = ∠C; ∠A + ∠B = 90°; ∠C = 90°; AB – гіпотенуза.

442.

Вправи 425 474

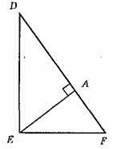
?DEF – прямокутний; EA ⊥ DF; ED і EF – катети.

443. α = 20° або α = 70°.

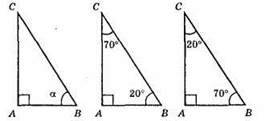
Вправи 425 474

444.

Вправи 425 474

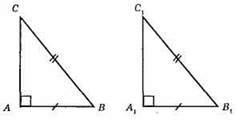
A) ∠A = ∠A1 = 90°. Трикутники рівні за катетом і гіпотенузою.

Вправи 425 474

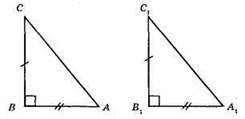
Б) Трикутники рівні за двома катетами.

445. Ні. Дві пари рівних катетів не можуть.

Рівні гіпотенузи можуть.

446.

Вправи 425 474

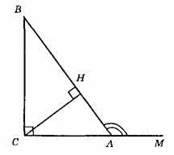
А) ∠A = 30°, ∠B = 60°;

Б) ∠BAM – найменший зовнішній кут? ABC. ∠BAM = 180° – ∠CAB = 180° – 30° = 150°;

В) CH – висота, ВС – висота, АС – висота, провели 1 відрізок.

447.

Вправи 425 474

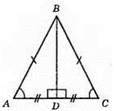
A) BD ⊥ AC; ?ABD = ?CBD – прямокутні; AB = BC, AD = DC;

Б) BD і DC – висоти прямокутного? BCD.

448.

Вправи 425 474

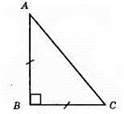
?ABC – рівнобедрений прямокутний трикутник. АС – основа, ∠А = ∠С. ∠А + ∠С = 90°; ∠А = ∠С = 45°.

Відповідь: 45°, 45°, 90°.

449.

Вправи 425 474

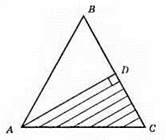
?ABC – рівносторонній, AB = ВС = АС; AD – медіана, бісектриса, висота; AD ⊥ ВС; ∠CDA = 90°; ∠А = ∠B = ∠С = 180° : 3 = 60°; ∠DCA = 60°; ∠DAC = 30°.

Відповідь: 60°, 30°, 90°.

450.

Вправи 425 474

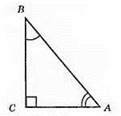
А) Нехай AB = х, тоді ∠А = 5х; х + 5х = 90°; 6х = 90°; х = 15°; ∠B = 15°, ∠А = 75°.

Б) ∠B = х; ∠А = х + 10°; х + х + 10° = 90°; 2х = 90° – 10° = 90°; 2х = 80°; х = 80°: 2; х = 40°; ∠B = 40°; ∠А= 50°.

451.

Вправи 425 474

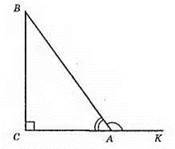
A) ∠ВАК = 130°; ∠ВАС = 180° – 130° = 50°; ∠СВА = 90° – 50° = 40°.

Відповідь: 40°, 50°.

Б) ∠А : ∠B = 2 : 7; 2х + 7х = 90°; 9х = 90° х = 90° : 9; х = 10°; ∠А = 20°; ∠B = 70°.

452.

Вправи 425 474

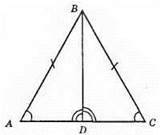
?ADB = ?CDB; ∠A = ∠C; ?ABC – рівнобедрений; ∠ADB = ∠CDB – суміжні рівні кути; ∠ADB = ∠CBD = 90°; AB = ВС; ?ADB = ?CBD за гіпотенузою і гострим кутом або за гіпотенузою AB і спільним катетом DB.

453.

Вправи 425 474

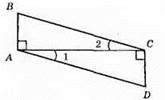
AD || ВС; ∠BAC = ∠DCA = 90°; ?ВАС = ?DCA; AB ⊥ АС; DC ⊥ АС; AB || DC, АС – січна; ∠1 = ∠2 – внутрішні різносторонні кути; АС – спільний катет. ?BAC = ?DCA за катетом і гострим кутом.

454. a)

Вправи 425 474

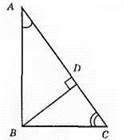
Точка D лежить між точками А і С.

455.

Вправи 425 474

456.

Вправи 425 474

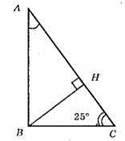
?ABC; ∠B = 90°; ВН ⊥ АС; ∠C = 25°; ∠BAH = 90° – 25° = 65°; ∠BHA = 90°; ∠ABH = 90° – 65° = 25°.

Відповідь: 65°, 25°, 90°.

457.

Вправи 425 474

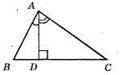
∠BAD = 38°; ∠CAB = 42°.

З? ABD: ∠ABD = 90° – 38° = 52°.

З? ADC; ∠ACD = 90° – 42° = 48°.

∠BAC = 38° + 42° = 80°.

Відповідь: 52°, 48°, 80°.

458.

Вправи 425 474

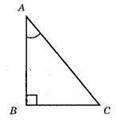
∠A = 45°; ?ABC – прямокутний рівнобедрений трикутник; ∠A = ∠C = 90° – 45° = 45°. Отже, АВ = ВС = 8 см.

Відповідь: ВС = 8 см.

459.

Вправи 425 474

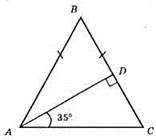
?ABC – рівнобедрений; AB = ВС; AD ⊥ ВС, AD – висота; ∠DAC = 35°; ?ADC – прямокутний; ∠DAC = 90° – 35° = 55°; ∠BAC = ∠DCA = 55°; ∠ABC = 180° – (55° + 55°) = 180° – 110° = 70°.

Відповідь: 55°, 55°, 70°.

460.

Вправи 425 474

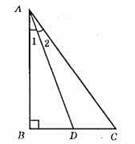
?ABC; ∠B = 90°; ∠D – бісектриса кута A; ∠1 = ∠2; ∠ADB = 74°; ?ABD; ∠BAD = 90° – 74° = 16°; ∠BAC = 32°; ∠BCA = 90° – 32° = 58°.

Відповідь: 32°, 90°, 58°.

461.

Вправи 425 474

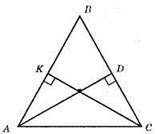
?АВС; СК ⊥ AB; AD ⊥ ВС; ?АКС = ?CDA – прямокутні трикутники; АС – спільна сторона; CK = AD за умовою. З їх рівності маємо: ∠BAC = ∠BCA, а це кути при основі АС, тому? ABC – рівнобедрений.

462. Якщо трикутник рівнобедрений, то висоти, проведені до бічних сторін, рівні. ?АКС = ?ADC; ∠A = ∠C; АС – спільна сторона. Прямокутні трикутники рівні за гіпотенузою і катетом. З цієї рівності маємо: AD = СК, а це висоти, проведені до бічних сторін.

463.

Вправи 425 474

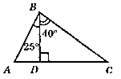
?ABC; BD ⊥ AC; ?ABD; ∠BAD = 90° – 25° = 65°; ?BDC; ∠BCD = 90° – 40° = 50°; ∠ABC = 25° + 40° = 65°.

Відповідь: 65°, 65°, 50°.

Вправи 425 474

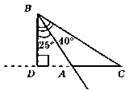
∠ABC = 40° – 25° = 15°; ∠BCA = 90° – 40° = 50°; ∠BAC = 180° – 15° – 50° = 115°.

Відповідь: 15°, 50°, 115°.

464.

Вправи 425 474

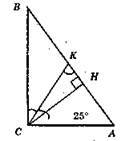
?ABC; ∠C = 90°; СК – бісектриса; ∠BCK = ∠ACK = 45°; ∠A = 180° – 70° – 45° = 65°; CH ⊥ AB; CH – висота; ∠HCA = 90° – 65° = 25°; ∠HCB = 90° – 25° = 65°.

Відповідь: 65°, 25°.

465.

Вправи 425 474

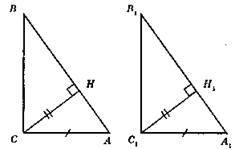
Дано: ?ABC і? A1B1C1 – прямокутні; ∠C = ∠C1 = 90°; АС = A1C1; CH ⊥ SA; C1H1 ⊥ B1A1; CH = C1H1.

?CHА = ?C1H1A1 за катетом і гіпотенузою. З цієї рівності маємо: ∠A = ∠A1. ?АВС = ?A1B1C1 за катетом (АС = A1С1) і гострим кутом (∠A = ∠A1).

466.

Вправи 425 474

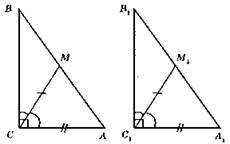
?АВС і? A1B1C1 – прямокутні. ∠C = ∠C1 = 90°; CM – бісектриса кута С, C1M1 – бісектриса кута С1; CM = C1М1.

?MCA = ?M1C1A1: 1) CM = С1М1; 2) С1А1 = СА; 3) ∠MCA = ∠M1C1A1 = 45°.

?MCA = ?М1С1А1 за двома сторонами і кутом між ними. З їх рівності маємо: ∠BAC = ∠B1A1C1. ?ВСА = ?В1С1А1 за катетом (АС = А1С1) і гострим кутом (∠A = ∠A1).

467.

Вправи 425 474

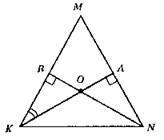
?KMN; KM = NM; KA ⊥ МN; NВ ⊥ МK; ∠KON = 140°; ∠BOK – суміжний ∠KON; ∠BOK = 180° – 140° = 40°.

З? ВОК: ∠BKO = 90° – 40° = 50°.

З? МКА: ∠KMA = 90° – 50° = 40°.

∠K = ∠N = (180° – ∠M) : 2 = (180° – 40°) : 2 = 70°.

Відповідь: 40°, 70°, 70°.

468.

Вправи 425 474

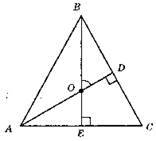
AB = ВС; AD ⊥ ВС; BE ⊥ АС; ?BOD – прямокутний; ∠EBD = 90° – 50° = 40°; BE – висота і бісектриса; ∠ABC = 40° х 2 = 80°; ∠A = ∠C = (180° – 80°) : 2 = 100° : 2 = 50°.

Відповідь: 80°, 50°, 50°.

469.

Вправи 425 474

?CAB – прямокутний; ∠CAB = 90°; АО – медіана; ВС – гіпотенуза. Продовжимо відрізок АО і відкладемо AD = АО.

470.

Вправи 425 474

?АОС – рівнобедрений; ∠1 = ∠2; ?АОВ – рівнобедрений; ∠3 = ∠4; ∠1 + ∠2 + ∠3 + ∠4 = 180°; ∠2 + ∠3 = 180° : 2; ∠2 + ∠3 = 90°, отже, ?АВС – прямокутний.

471.

Вправи 425 474

?ABC – прямокутний; CL – бісектриса; CH ⊥ AB, СН – висота; ∠HCL = 22°.

?СНА. ∠HCA = 45° – 22° = 23°; ∠HAC = 90° – 23° = 67°.

?ABC. ∠B = 90° – ∠A = 90° – 67° = 23°.

Відповідь: 67° і 23°.

472.

Вправи 425 474

?ABC; BL – бісектриса; ∠BAL = ∠CAL; AH ⊥ ВС; AH – висота; ∠LAH = ∠CAH = x; ∠CAL = ∠BAL = 2x; ?ABC – рівнобедрений; AB = BC; ∠A = ∠C;

?AHC; ∠C = 90° – x; 4x = 90° – x; 5x = 90°; x = 90° : 5 = 18°; ∠A = ∠C = 4 x 18° = 72°; ∠ABC = 180° – 72° – 72° = 36°.

Відповідь: 72°, 72°, 36°.

473.

Вправи 425 474

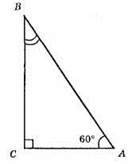
?ABC; ∠C = 90°; ∠A = 60°; AB – AC = 6 CM; ∠CBA = 90° – ∠BAC = 90° – 60° = 30°; AC – катет, що лежить проти кута 30°;

АС = 1/2AВ; AB = х; АС = x/2; x – x/2 = 6; 2x – x = 12; x = 12. AB = 12 см, АС = 6 см.

Відповідь: 12 см, 6 см.

474.

Вправи 425 474

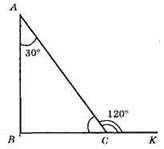
?ABC; ∠B = 90°; ∠ACK = 120° – зовнішній кут при вершині С. ВС + АС = 21 см; ∠ACB = 180° – ∠ACK = 180° – 120° = 60°; ∠BAC = 90° – 60° = 30°; ВС – катет, що лежить проти кута 30°; ВС =1/2АС.

Нехай ВС = х, тоді АС = 2х; х + 2х = 21; 3х = 21; х = 7; ВС = 7 см, АС = 14 см.

Відповідь: 7 см, 14 см.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  2. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  3. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  4. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  5. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  6. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  7. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  8. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  9. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  10. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  11. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  12. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  13. Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...

  14. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  15. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  16. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  17. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  18. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  19. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  20. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  21. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  22. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  23. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  24. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  25. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  26. Запитання і вправи для повторення § 7 Відповідь: (3; 3), (-1; -2), (1; 0,5). 1012. а) х – 2y = 4; X 0 4 Y -2 0 Б) 4х + у = -4; X 0 -1 Y -4 0 В) 3х – 2y = 6. X 0 2 У -3 0 Відповідь: пара чисел (-2; 3) не являється розв’язком системи рівнянь Х […]...

  27. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  28. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  29. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  30. Вправи для повторення розділу 1 До § 1. 617. Цілі раціональні вирази: Дробові раціональні вирази: А + с 618. 50а кг завезли цукру. Якщо а = 12, то 50а = 50 • 12 = 600 (кг). До § 2. 624. n, n + 1, n + 2 – три послідовні цілі числа; N + (n + 1) + (n + […]...

  31. Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...

  32. Вправи для повторення розділу 3 До § 22. 1116. 1) х + 3 = 2; -5 + 3 = 2; -2 ≠ 2; ні; 2) 2 – х = 7; 2 – (-5) = 7; 7 = 7; -5 є коренем рівняння; 3) х : 5 = 1; -5 : 5 = 1; -1 ≠ 1; ні; 4) 4х = […]...

  33. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  34. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  35. Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...

  36. Тренувальні вправи на використання прикметників у мовленні. Практичні словотворчі вправи. Усний опис зимового пейзажу Урок 65 Тема. Тренувальні вправи на використання прикметників у мовленні. Практичні словотворчі вправи. Усний опис зимового пейзажу Мета: вдосконалювати вміння рід, число і відмінок у сполученні з іменником, вміння добирати прикметники-синоніми, повторити правило перевірки ненаголошеного голосного у корені слова; розвивати словотворчі вміння дітей, усне мовлення; виховувати любов до природи. Обладнання: картинки зимової природи, словники синонімів, […]...

  37. Вправи на вживання різних відмінкових форм прикметників у множині. (Вправи 210-212) Тема. Вправи на вживання різних відмінкових форм прикметників у множині. (Вправи 210-212). Мета. Вчити школярів правильно вимовляти і вживати на письмі закінчення прикметників, орієнтуючись на кінцевий приголосний основи. Обладнання: експозиція дитячих квітів-розмальовок, таблиця “Почуття”, таблиця-ватман “Словничок”. Хід уроку I. Організація класу. II. Перевірка домашнього завдання. 1. Вправа “Крісло автора”. Діти зачитують твори про мамині (бабусині) […]...

  38. Вправи на визначення роду і числа прикметників за іменниками. (Вправи 168-170) Тема. Вправи на визначення роду і числа прикметників за іменниками. (Вправи 168-170). Мета. Виявити істотну відмінність між прикметниками та іменниками як частинами мови: кожний прикметник залежно від іменника може змінюватись не тільки за числами і відмінками, а й за родами; вчити розпізнавати рід прикметників за родом іменників та формальними ознаками – родовими закінченнями. Обладнання: таблиця […]...

  39. Вправи на визначення відмінка прикметника у реченні за відмінком іменника. Контрольна робота: списування. (Вправи 179-181) Тема. Вправи на визначення відмінка прикметника у реченні за відмінком іменника. Контрольна робота: списування. (Вправи 179-181). Мета. Вчити учнів за допомогою відмінкової форми іменників визначати відмінок прикметників у реченнях, виховувати шанобливе ставлення до Батьківщини. Обладнання: вірші, прислів’я про Батьківщину, запис “Пісні про рушник” на сл. А. Малишка, індивідуальні картки з текстом пісні. Хід уроку I. […]...

  40. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

Ви зараз читаєте: Вправи 425-474
«
»