Застосування похідної
Математика – Алгебра
Похідна
Застосування похідної
Нехай функція 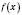 визначена на проміжку
визначена на проміжку 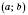 і
і 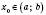 .
.
Функція називається Зростаючою в точці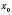 , якщо існує інтервал
, якщо існує інтервал 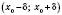 , де
, де 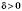 , який міститься у проміжку
, який міститься у проміжку 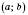 і є таким, що
і є таким, що 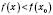 для всіх x з інтервалу
для всіх x з інтервалу 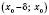 і
і 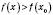 для всіх x з інтервалу
для всіх x з інтервалу
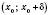 .
.Функція називається Спадною в точці
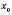 , якщо існує інтервал
, якщо існує інтервал 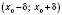 , який міститься в проміжку
, який міститься в проміжку 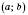 і є таким, що
і є таким, що 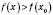 для будь-якого x з інтервалу
для будь-якого x з інтервалу 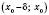 і
і 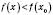 для будь-якого x з інтервалу
для будь-якого x з інтервалу 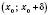 .
.Означення точок екстремуму описано в розділі “Алгебра. 10 клас”.
Якщо функція
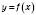 зростаюча (спадна) у кожній точці проміжку
зростаюча (спадна) у кожній точці проміжку 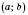 , то вона зростаюча (спадна) на цьому проміжку.
, то вона зростаюча (спадна) на цьому проміжку.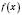 в кожній точці інтервалу
в кожній точці інтервалу 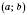 має похідну
має похідну 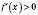
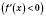 , то функція зростає (спадає) на
, то функція зростає (спадає) на 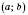 .
.Зверніть увагу:
1) Якщо функція f є неперервною в якомусь із кінців інтервалу
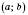 , то цю точку можна приєднати до інтервалу зростання (спадання).
, то цю точку можна приєднати до інтервалу зростання (спадання).2) Для розв’язування задач зручно користуватися таким твердженням: точки, у яких похідна дорівнює 0 або не існує, поділяють область визначення функції f на проміжки, у кожному з яких
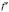 зберігає незмінний знак.
зберігає незмінний знак.Внутрішня точка області визначення функції, у якій похідна дорівнює нулю або не існує, називаються Критичною точкою функції.
Внутрішня точка області визначення, у якій
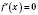 , називається Стаціонарною точкою функції.
, називається Стаціонарною точкою функції.Теорема 2. Якщо функція
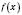 у внутрішній точці області визначення має екстремум, то в цій точці похідна
у внутрішній точці області визначення має екстремум, то в цій точці похідна 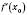 , якщо вона існує, дорівнює нулю.
, якщо вона існує, дорівнює нулю.Теорема 3. Якщо функція f є неперервною в точці
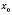 , а
, а 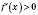 на інтервалі
на інтервалі 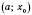 і
і 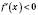 на інтервалі
на інтервалі 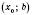 , то точка
, то точка 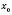 є точкою максимуму функції.
є точкою максимуму функції.Теорема 4. Якщо функція f є неперервною в точці
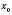 , а
, а 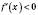 на інтервалі
на інтервалі 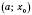 і
і 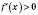 на інтервалі
на інтервалі 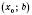 , то точка
, то точка 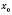 є точкою мінімуму функції f.
є точкою мінімуму функції f.Теорема 5. Нехай точка
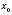 є стаціонарною для функції
є стаціонарною для функції 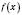 і нехай в цій точці існує похідна другого порядку
і нехай в цій точці існує похідна другого порядку 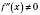 . Тоді, якщо
. Тоді, якщо 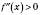 , то
, то 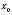 є точкою мінімуму і, якщо
є точкою мінімуму і, якщо 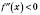 , то
, то 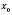 є точкою максимуму функції
є точкою максимуму функції 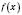 .
.Найбільше і найменше значення функції на відрізку
Щоб знайти найбільше (найменше) значення неперервної функції на відрізку 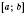 , треба знайти всі локальні максимуми (мінімуми) і порівняти їх зі значеннями функції, яких вона набуває на кінцях відрізка. Найбільше (найменше) число серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку
, треба знайти всі локальні максимуми (мінімуми) і порівняти їх зі значеннями функції, яких вона набуває на кінцях відрізка. Найбільше (найменше) число серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку 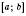 .
.
Позначення: 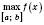 ;
; 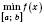 .
.