Координати і вектори у просторі
776.
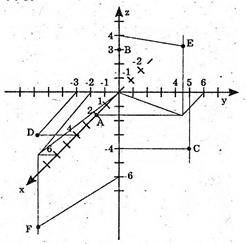
А(2; 0; 0), В(0; 0; 3), С(0; 5; -4),
D(4; -3; 0), Е(2; 6; 4), F(6; -2; -6).
777.
А(2; 0; 5), В(-4; 0; 2), С(4; 0; -2), D(1; 3; 1),
A? хОz, В? xОz, C? xOz.
Основа тетраедра ABC лежить у координатній площині хОz,
Тому що yА = yB = yC = 0.
778.
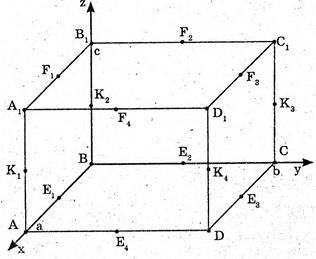
А) Координати вершин паралелепіпеда ABCDA1B1C1D1
А(2; 0; 0) В(0; 0; 3) С(0; 5; -4)
D(4; -3; 0) E(2; 6; 4) F(6; -2; -6).
Б) Середини його ребер: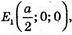 
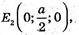
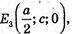
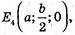
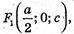
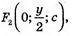
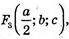
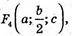
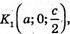
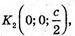
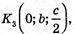
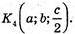
779.
А) А(-1; 0; 6), В( 1; 2; 10); т. Е(0; 1; 8);
АЕ = BE
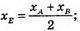
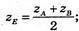
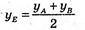
Б) A(0; 4; -6), В(2; 2; 2)
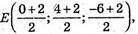E(1; 3; -2);
В) А(-2; 4; 2), В(-2; -4; 2)
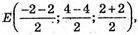Е(-2; 0; 2).
780.
СЕ = ED
А) С(-4; 0; 2), D(4; 0; -2)
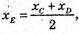
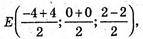Е(0; 0; 0).
Початок координат є серединою відрізка CD.
Б) С(-4; 2; -8), D(4; -2; -8)
Е(0; 0; -8).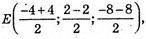 
Початок координат не є серединою відрізка CD.
781.
ME = EN
А) М(2; 4; -6), N(-2; 7; 6);
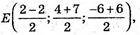
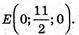
Середина т. Е відрізка MN лежить на осі Оy.
Б) М(-3; 0; 7), N(-3; 0; -7); Е(-3; 0; 0).
Середина відрізка MN лежить на осі Ох.
782.
КЕ = EР
А) К(1; 1; 4), Р(4; 0; -4);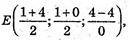 
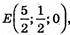Е? xОу;
Б) К(-6; 2; 4), Р(5; -2; 3);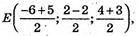 
Р? xΟz.
783.
АС = СВ
А(8; -5; -4), С(2; 1; 10); В(хB; уB; zB).
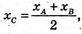
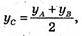
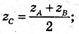
XB = 2xC – xA; yB = 2 yC – y A; zB = 2 zC – z A;
XB = 2 × 2 – 8 = -4; yB = 2 × 1 + 5 = 7;
ZB = 2 × 10 + 4 = 24
B(-4; 7; 24).
784.
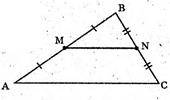
В(-2; 0; 4), М(3; 9; -2), N(-1; -4; 0);
A(хA; уA; zA) = ? C(xс; yс zc)= ?
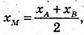xA = 2 × xM – xB, 
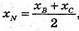хC =2 × xN – xB;
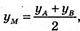yA = 2 × yM – yB, 
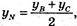yC =2 × yN – yB;
X A = 2 × 3 + 2 = 8, у A = 2 × 9 – 0 = 18;
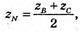zC =2 × zN – zB;
Аналогічно: zA = 2 × zM – z B, zА= 2 × (-2) – 4 = -8;
ХC = 2 × (-1) + 2 – 0, yC = 2 × (-4) – 0 = -8, zC = 2 × 0 – 4 = -4.
А(8; 18; -8), С(0; -8; -4).
785.
А) А(-1; -3; 18), В(-2; 2; 12), С(3; 3; -10), D(4; -2; -4);
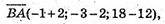
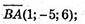
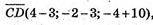
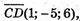
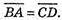
Чотирикутник ABCD є паралелограм.
Б) А(4; -2; -6), В(-6; 2; 8), С(2; -3; 9), В(12; -7; -4);
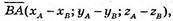
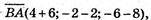
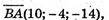
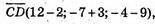
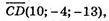
Чотирикутник ABCD не є паралелограм.
786.
А) А(2; 4; -1), В(1; -3; -2), С(-6; 2; 1)
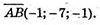
С(-6; 2; 1)
D(XD; yD; zD)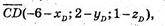 
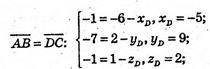D(-5; 9; 2).
Відповідь: D(-5; 9; 2).
Б) A(-7; 5; 4), В(1; 5; 2), C(9; -3; 88), D(xP; yP; zP) = ?
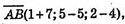
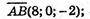
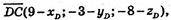
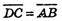
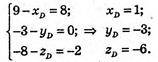
Відповідь: D(1; -3; -6).
787.
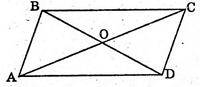
A(-1; 8; -2), B(-4; 6; 5), O(1; 0; 2), C(xC; yC; zC) = ?, D(xP; yP; zP) = ?
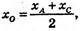xC = 2 × xO – xA, xC = 2 × 1 + 1 = 3;
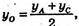yC = 2 × yO – yA, yC = 2 × 0 – 8 = 8;
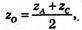zC = 2 × zO – zA, zC = 2 × 2 + 2 = 6.
C(3; -8; 6).
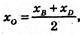xD = 2 × xO – xB, xD = 2 × 1 + 4 = 6; xD = 6;
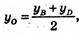yD = 2 × yO – yB, yD = 2 × 0 – 6 = -6; yD = -6;
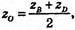zD = 2 × zO – zB, zD = 2 × 2 -5 = -1; zD = -1;
D(6; -6; -1).
Відповідь: C(3; -8; 6), D(6; -6; -1).
788.
B(-2; 6; 3), К(3; 4; -2), ВК = ?
BK2 = (3- (-2))2 + (4 – 6)2 + (-2 – 3)2 = 25 + 4 + 25 = 54;
BK2 = 54;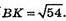 
789.
A(2; -1; -5), B(-2; 1; 6), О(0; 0; 0).
AO2 = 22 + (-1)2 + (-5)2 = 4 + 1 + 25 = 30;
BO2 = (-2)2 + 12 + 62 = 4 + 1 + 36 = 41;
BO2 > AO2.
До початку координат ближче лежить точка А.
790.
А(1; 2; 3), В(2; 3; 4), С(3; 4; 5)
АВ2 = (2 – 1)2 + (3 – 2)2 + (4 – З)2 = 1 + 1 + 1 = 3; АВ2 = 3;
АС2 = (3 – 1)2 + (4 – 2)2 + (5 – З)2 = 4 + 4 + 4 = 12; АС2 = 12;
ВС2= (З – 2)2 + (4 – 3)2 + (5 – 4)2 = 1 + 1 + 1 = 3; ВС2 = 3.
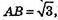
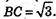
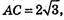АС = АВ + ВС.
Точки А, В, С не є вершинами трикутника.
791.
А(1; -2; 3), В(-2; 3; 1), С(3; 1; -2), РΔABC = ?
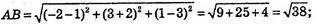
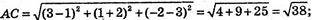
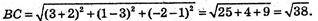
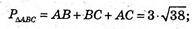
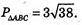
792.
М(0; 1; 1), N(2; -1; 3), Р(-1; k; 0), k = ?
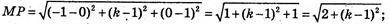
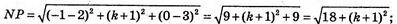
МР2 = NP2; 2 + (k – 1)2 = 18 + (k + 1)2;
2 + k2 -2k + 1 = 18 + k2 + 2k + 1; 4k = -16; k = – 4.
793.
A(4; -1; 3) B(1; 3; 0), M(0; y ;0), y = ?
MA = MB.
МA2 = 42 + (-1 – y)2 + 32 = 25 + (у + 1)2;
MB2 = (1 – 0)2+ (3 – y)2+ 02 = 1 + (y – 3)2;
25 + (у + 1)2 = 1 + (у – 3)2; 25 + у2+ 2y + 1 = 1 + y2 – 6y + 9;
8у = -16, у = -2. M(0; -2; 0).
794.
A(-2; 3; 6), B(2; 3; -1), C(4; 1; 0);
BM = ? ΑM = CM. M (xM, yM)·
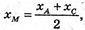
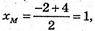хM = 1;
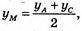
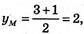yM = 2;
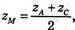
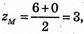zM =3·
M(1; 2; 3); В(2; 3; -1)
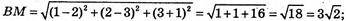
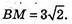
795.
А(2; -4; 2), С(0; 0; 6), M(1; 2; 4),
ВМ = CM, AN = CN. BN =?
N? N(XN, yN, zN),
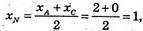хN = 1;
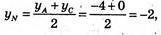yN =-2;
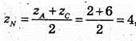zN = 4;
N(1; -2; 4)
В? В(хB; уB; zB),
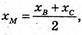хB = 2 × хM – хC = 2 × 1 – 0 = 2, хB = 2;
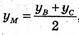yB = 2 × yM – yC = 2 × 2 – 0 = 4, yхB = 4;
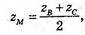zB = 2 × zM – zC = 2 × 4 – 6 = 2, хB = 2;
В(2; 4: 2).
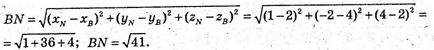
796.
А) А(5; 0; 0), В(0; 5; 0), С(0; 0; 5).
РΔABC = ? SΔABC = ? Вид трикутника ABC?
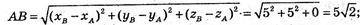
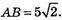
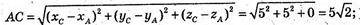
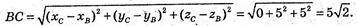
ΔАВС: АВ = АС = ВС. ΔABC – рівносторонній.
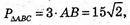
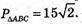
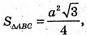
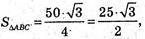
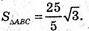
Б) А(-2; 0; 5), В(3; 4; 0), С(-2; 4; 0).
Вид трикутника ABC? PΔABC = ? SΔABC = ?
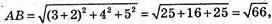
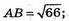
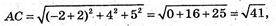
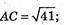
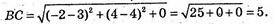
ВС2 + АС2 = 25 + 41 = 66, АВ2 = 66;
ВС2 + АС2 = АВ2, АВ2 = АС2 + ВС2.
ΔАВС – прямокутний, ΔАСВ = 90°.
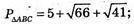
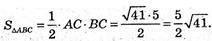
В) А(2; 4 -1), В(-1; 1; 2), С(5; 1; 2).
Вид трикутника ABC? РΔABC = ? PΔABC = ?
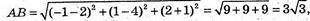
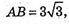АВ = с;
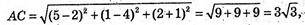
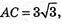АС = b;
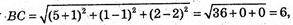ВС = 6, ВС = а.
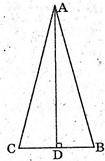
ΔABC: AB = АС. ΔАВС – рівнобедрений.
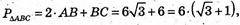
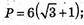
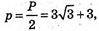а = ВС = 6,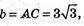 
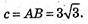
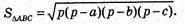
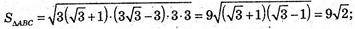
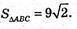
797.
А) М(0; -2; 0), N(4; 1; 0), Р(4; 1; 5), К(0; -2; 5).
Вид чотирикутника MNPK? SMNPK = ?
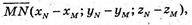
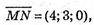
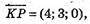
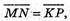тобто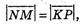 
MN ¦ KР.
Якщо дві протилежні сторони чотирикутника рівні
І паралельні, то цей чотирикутник – паралелограм.
MNPK – паралелограм.
(1 votes, average: 5.00 out of 5)
Loading...