Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Координати вектора

Координати вектора

УРОК № 43

Тема. Координати вектора

Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач.

Тип уроку: комбінований.

Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].

Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач.

Хід уроку

I. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та

відповісти на запитання, які виникли в учнів під час його виконання.

Фронтальна бесіда

1) Що таке вектор? Як позначаються вектори? 2) Які вектори називаються однаково напрямленими (протилежно напрямленими)? 3) Що таке абсолютна величина вектора? 4) Що таке нульовий вектор? 5) Які вектори називаються рівними? Яку властивість мають рівні вектори? 6) Скільки різних векторів можна відкласти від заданої точки, які дорівнюють даному вектору?

II. Сприймання й усвідомлення нового матеріалу

Поняття координат вектора

Координати вектора Координати вектора, що має початок у точці А і кінець у точці В, дорівнюють

різниці координат точок В і А.

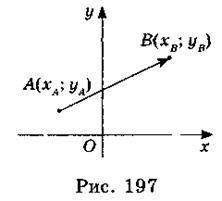
Якщо початок вектора Координати вектора є точка А(хА; уА), а кінець вектора – точка В(хВ; уВ), то Координати вектора(хВ – хА; уВ – уА) (рис. 197).

Координати вектора

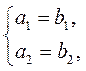Рівні вектори мають рівні координати. Якщо відповідні координати векторів однакові, то вектори рівні. Якщо Координати вектора(a1; a2) = Координати вектора(b1; b2), то Координати вектора і навпаки, якщо 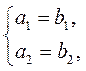Координати вектора, то Координати вектора(a1; a2) = Координати вектора(b1; b2).

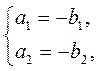Протилежні вектори мають протилежні відповідні координати. Якщо відповідні координати двох векторів протилежні, то вектори протилежні. Якщо Координати вектора(a1; a2), Координати вектора(b1; b2) і Координати вектора = –Координати вектора, то Координати вектора і навпаки.

Довжина вектора дорівнює квадратному кореню із суми квадратів його координат. Якщо задано вектор Координати вектора(a1; a2), то Координати вектора.

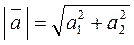Розв’язування вправ

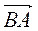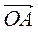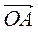1) Дано точки А(2; 3), B(1; 1). Які координати мають вектори Координати вектора і Координати вектора? 2) Знайдіть координати вектора Координати вектора, якщо А(5; 1) і О – початок координат. 3) Коли вектор Координати вектора(1; 2) відклали від початку координат, то дістали вектор Координати вектора. Знайдіть координати точки А. 4) Знайдіть 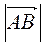Координати вектора, якщо А(1; 2), В(-3; -2). 5) Дано точки: А(3; -2), В(-4; 6), С(-2; -6), D(x; y). 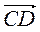Знайдіть х і у, якщо Координати вектора = Координати вектора.

III. Закріплення й осмислення нового матеріалу

Розв’язування задач

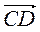1. Від точки А відкладено вектор Координати вектора = Координати вектора. Знайдіть координати точки А, якщо В(-1; 5), Координати вектора(1; 3). 2. Який із векторів Координати вектора(2; 4), Координати вектора(-1; 3) має більшу довжину? 3. Дано точки A(0; 1), B(1; 0), C(1; 2), D(2; 1). Доведіть рівність векторів Координати вектора і Координати вектора. 4. Дано три точки A(1; 1), В(-1; 0), C(0; 1). 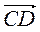Знайдіть таку точку D(x; y), щоб виконувалася рівність Координати вектора = Координати вектора.

IV. Домашнє завдання

1. Вивчити теоретичний матеріал. 2. Розв’язати задачу.

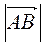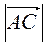Знайдіть Координати вектора, якщо А(3; 2), В(-3; -4). Знайдіть координати точки С(0; у), якщо Координати вектора = Координати вектора.

V. Підбиття підсумків уроку

Заповніть пропуски в тексті.

Координатами вектора з початком у точці А(хА; уА) і кінцем у точці В(хB; уB) будуть числа х = …, у = …. Рівні вектори мають рівні…, і навпаки, … . Модуль вектора Координати вектора(a1; a2) дорівнює….


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...

  2. Множення вектора на число УРОК № 47 Тема. Множення вектора на число Мета уроку: формування вміння множити вектор на число; вивчення властивостей множення вектора на число; формування вмінь застосовувати вивчені значення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують множення вектора на число; […]...

  3. Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...

  4. Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...

  5. Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...

  6. Множення вектора на число Геометрія Вектори Множення вектора на число Добутком вектораНа число називається вектор , тобто . Для будь-якого вектора і чисел і . Для будь-яких двох векторів і і числа . Теорема 1. Абсолютна величина вектора дорівнює . Напрям вектора , якщо , збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо . […]...

  7. Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...

  8. Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...

  9. Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...

  10. Колінеарні вектори УРОК № 48 Тема. Колінеарні вектори Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та […]...

  11. Координати середини відрізка УРОК № 23 Тема. Координати середини відрізка Мета уроку: виведення формул для знаходження координат середини відрізка та формування вмінь учнів застосовувати ці формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують та доводять формули координат середини відрізка. Застосовують вивчені формули […]...

  12. Координати векторa Геометрія Вектори Координати векторa Нехай вектор має початком точку , а кінцем – точку . Координатами вектора називаються числа і . Позначення: або . . Очевидно, що . Теорема. Вектори рівні тоді й тіль­ки тоді, коли вони мають рівні відповідні координати....

  13. Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...

  14. Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...

  15. Розкладання вектора за координатними осями Геометрія Вектори Розкладання вектора за координатними осями Вектор називається Одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають напрями додатних координатних півосей, називаються Координатними векторами, або Ортами (див. рисунок). Позначення: ; . Оскільки координатні вектори відмінні від нуля й неколінеарні, то будь-який вектор можна розкласти за цими векто­рами: ....

  16. Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...

  17. Тематична контрольна робота № 5 УРОК № 51 Тема. Тематична контрольна робота № 5 Мета уроку: контроль навчальних досягнень учнів з мети “Вектори”. Тип уроку: комбінований. Вимоги до рівня підготовки учнів: застосовують означення та властивості геометричних фігур при розв’язуванні задач. Хід уроку І. Тематичне оцінювання № 5 Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. Наводимо текст […]...

  18. Тематичне оцінювання № 6 Урок 61 Тема. Тематичне оцінювання № 6 Мета уроку: перевірка навчальних досягнень учнів з теми “Кути та вектори у просторі”. Тематичне оцінювання № 6 можна провести шляхом виконання те­матичної контрольної роботи. І. Тематична контрольна робота № 6 Варіант А 1. Сторона квадрата ОАВС дорівнює 5 (рис. 303). Запишіть координа­ти вектора . (3 бали) 2. Із […]...

  19. Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...

  20. Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...

  21. Віднімання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри 3.3. Віднімання векторів Різницею двох векторів, спрямованих по одній прямій або паралельних один одному, є алгебраїчна різниця цих векторів. Щоб знайти різницю двох векторів, які мають різні напрями, треба розмістити обидва вектори так, щоб вони виходили з однієї точки. Потім сполучити кінці векторів вектором, спрямованим від від’ємника до зменшуваного. Цей вектор […]...

  22. Координати – Кінематика 5. Механіка 5.1. Кінематика 5.1.5. Координати Координати точки – це числа, які визначають положення фізичного тіла (матеріальної точки) на площині чи в просторі. В декартовій системі координат положення тіла (матеріальної точки) на лінії площини і в просторі визначається відповідно однією (а), двома (б) або трьома (в) координатами (X, Y, Z)....

  23. Тематичне оцінювання № 5 Урок 52 Тема. Тематичне оцінювання № 5 Мета уроку: перевірити навчальні досягнення учнів з теми “Декартові координати у просторі”. Хід уроку Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 5 Варіант А 1. Чи лежать точки А, В, С на одній прямій, якщо А(1;1;-3), В (-1;3;5), С […]...

  24. ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 1. ОСНОВИ КІНЕМАТИКИ 1.2. ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Вектор – напрямлений відрізок. Векторні величини мають числове значення (модуль), напрям, точку прикладання (рис. 3). Рис. З Проекція вектора на вісь Ох – довжина відрізка, який сполучає проекцію початку вектора на вісь Ох з проекцією кінця вектора на ту саму […]...

  25. Прямокутна система координат на площині УРОК № 22 Тема. Прямокутна система координат на площині Мета уроку: узагальнення та систематизація матеріалу про декартову прямокутну систему координат. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують прямокутну систему координат. Застосовують вивчені означення до розв’язування задач. Хід уроку I. Перевірка домашнього завдання […]...

  26. Розв’язування задач координатно-векторним методом 1. 1) Введемо прямокутну систему координат із початком у точці В і спрямуємо вісь Оx вздовж ребра BA, Oz – вздовж ВВ1. Довжину ребра куба позначимо як а. Тоді координати точок: А(а; 0; 0;); С(0; а; 0); R(а; а; 0); C1(0; а; а). Знайдемо координати векторів і Знайдемо довжини векторів: Знайдемо кут між векторами: Кут […]...

  27. Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  28. Прямокутна система координату просторі Урок 44 Тема. Прямокутна система координату просторі Мета уроку: знайомство з декартовою прямокутною системою координат у просторі. Обладнання: модель куба. Хід уроку І. Аналіз виконання тематичного оцінювання II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення й виконання домашнього завдання. III. Сприйняття й усвідомлення нового матеріалу Прямокутна система координат на […]...

  29. Декартові координати у просторі – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Декартові координати у просторі М – точка у просторі М(х, у, x) Мхy – проекція точки М на площину хоу; Мхy(х, о, у) Мх, Му, Mz – проекції точки М на осі OX, OY, OZ відповідно. Мх(х, о, о); Му(о, у, о); Мz(о, о, z). Відстань між точками А(x1,y1,z1) і […]...

  30. Відстань між двома точками простору Урок 45 Тема. Відстань між двома точками простору Мета уроку: виведення формул для знаходження відстані між двома точками, заданих координатами, та застосування формули до розв’язування задач. Обладнання: схема “Відстань між двома точками”, модель куба. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Ребро куба дорівнює 10: варіант 1 […]...

  31. Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано коорди­натами? 2) Як […]...

  32. Проекція вектора на координатну вісь – Елементи векторної алгебри 3. Елементи векторної алгебри 3.5. Проекція вектора на координатну вісь Довжину відрізка A1B1 між проекцією початку вектора а і кінця вектора на вісь, взяту зі знаком ” + ” або “-“, називають проекцією вектора на координатну вісь. Проекція додатна, коли напрям руху від проекції початку вектора до проекції кінця збігається із напрямом координатної осі, і […]...

  33. Додавання векторів за правилом паралелограма – Елементи векторної алгебри 3. Елементи векторної алгебри 3.2. Додавання векторів за правилом паралелограма Щоб додати два вектори за правилом паралелограма, треба розмістити їх так, не змінюючи їх напряму, щоб вони виходили з однієї точки, й добудувати на кінцях векторів паралельні прямі. Діагональ одержаного паралелограма, проведена з точки, в якій суміщені початки обох векторів, є їх сумою....

  34. Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...

  35. Відстань між двома точками із заданими координатами УРОК № 24 Тема. Відстань між двома точками із заданими координатами Мета уроку: виведення формули для знаходження відстані між двома точками, заданими координатами, і застосування формул до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і доводять формулу для знаходження відстані […]...

  36. Розв’язування задач геометричного змісту Урок № 126 Тема. Розв’язання задач геометричного змісту 1. На координатній прямій позначте точку D(-3) і точку С, щоб довжина CD дорівнювала 2,5 одиничних відрізки. Визначте координату точки С. Скільки розв’язків має задача? 2. Знайдіть площу і периметр чотирикутника ABCD, якщо A(-1; 2); B(3; 2); С(3; -4); D(-1; -4). 3. Знайдіть площі заштрихованих фігур, зображених […]...

  37. Прискорення. Прискорення при криволінійному русі – КІНЕМАТИКА ФІЗИКА Частина 1 МЕХАНІКА Розділ 1 КІНЕМАТИКА 1.3. Прискорення. Прискорення при криволінійному русі Градієнт швидкості матеріальної точки V з часом £ характеризують прискоренням Прискорення виражається в метрах на секунду в квадраті (СІ) та сантиметрах на секунду в квадраті (СГС). При прямолінійному русі вектор швидкості напрямлений уздовж однієї й тієї самої прямої – траєкторії, внаслідок чого […]...

  38. Координати середини відрізка Геометрія Декартові координати на площині Координати середини відрізка Якщо , – довільні точки, – середина відрізка AB, то ; ....

  39. Рух точки по колу – КІНЕМАТИКА ФІЗИКА Частина 1 МЕХАНІКА Розділ 1 КІНЕМАТИКА 1.4. Рух точки по колу Рух матеріальної точки по колу є окремим випадком криволінійного руху. Розглядаючи такі величини, як швидкість , прискорення , радіус-вектор , питання про вибір їхнього напряму не виникало, оскільки воно випливало з їхньої природи. Подібні вектори називають полярними. Вектори типу dφ, напрям яких пов’язаний […]...

  40. Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...

Ви зараз читаєте: Координати вектора
«
»