Головна ⇒ 📌Довідник з геометрії ⇒ Квадрат
Квадрат
Геометрія
Чотирикутники
Квадрат
Квадрат – це прямокутник, у якого всі сторони рівні.
Властивості квадрата
Оскільки квадрат є паралелограмом, прямокутником і ромбом водночас, маємо:
1) у квадрата всі сторони рівні;
2) у квадрата всі кути рівні;
3) діагоналі квадрата рівні, перетинаються під прямим кутом, діляться в точці перетину навпіл, є бісектрисами його кутів;
4) діагоналі квадрата ділять його на чотири рівні рівнобедрені прямокутні трикутники.
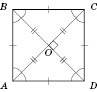
На рисунку ABCD – квадрат. AB = = BC =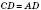 ;
; 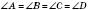 ;
; 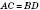 ;
; 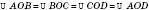 .
.
Ознаки квадрата
Теорема 1. Якщо в чотирикутника всі сторони і всі кути рівні, то він є квадратом.
Теорема 2. Якщо діагоналі прямокутника перетинаються під прямим кутом, то він є квадратом.
Теорема 3. Якщо діагоналі ромба рівні, то він є квадратом.
Related posts:
- Ромб Геометрія Чотирикутники Ромб Ромб – це паралелограм, у якого всі сторони рівні. Властивості ромба Оскільки ромб є паралелограмом, він має всі властивості паралелограма і деякі інші. Теорема 1. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів. На рисунку ABCD – ромб; ; ; ; ; . Теорема 2. Діагоналі ромба розбивають […]...
- Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...
- Квадрат – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Квадрат Діагоналі взаємноперпендикулярні, рівні і в точці перетину діляться навпіл. Всі внутрішні кути прямі. Всі сторони рівні....
- Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...
- Ромб. Квадрат Урок № 9 Тема. Ромб. Квадрат Мета: працювати над засвоєнням учнями змісту означень, властивостей та ознак ромба і квадрата. Формувати вміння: – відтворювати вивчені твердження; – застосовувати властивості, ознаки ромба і квадрата до розв’язування типових задач; – застосовувати властивості, ознаки ромба і квадрата разом із раніше вивченими твердженнями в темі “Чотирикутники” до розв’язування задач підвищеного […]...
- Прямокутник Геометрія Чотирикутники Прямокутник Прямокутник – це паралелограм, у якого всі кути прямі. Властивості прямокутника Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма і ще деякі інші. Теорема. Діагоналі прямокутника рівні. На рисунку . . ; – рівнобедрені. Ознаки прямокутника Теорема 1. Якщо в чотирикутнику всі кути рівні, то він є прямокутником. Теорема 2. Якщо […]...
- Теорема Піфагора Геометрія Трикутники Теорема Піфагора Теорема 1 (Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Правильною є і теорема, обернена до теореми Піфагора. Теорема 2 (обернена). Коли в трикутнику сторони a, b, c і , то цей трикутник є прямокутним з гіпотенузою c. Теорема 3. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу. […]...
- Прямокутник. Квадрат Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 22. Прямокутник. Квадрат На рисунку 156 зображено чотирикутник, у якого всі кути прямі. Такий чотирикутник, як відомо з молодших класів, називається прямокутником. Протилежні сторони прямокутника рівні між собою, тобто АВ = DC і AD = ВС. Сторони прямокутника, які не є протилежними, […]...
- Паралелограм Геометрія Чотирикутники Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника. Вершини чотирикутника називаються Сусідніми, якщо […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- КВАДРАТ ДВОЧЛЕНА РОЗДІЛ 3 МНОГОЧЛЕНИ &11. КВАДРАТ ДВОЧЛЕНА Ви вже знаєте, як додавати, віднімати і множити многочлени. Як і числа, многочлени можна підносити до степеня з натуральним показником. Для цього достатньо помножити многочлен на себе стільки разів, скільки показує число в показнику степеня. В окремих випадках піднесення до степеня дозволяє спрощувати дії з многочленами. Розглянемо їх. Запам’ятайте! […]...
- Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібності випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Рівність фігур Геометрія Рух Рівність фігур Дві фігури називаються Рівними, якщо вони переводяться рухом одна в одну. Теорема. Рівні трикутники (означення дивись у розділі “Геометрія.”) є рівними фігурами, тобто суміщаються рухом....
- КВАДРАТ. ПЕРИМЕТР КВАДРАТА ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ВИРАЗИ З ДУЖКАМИ Урок 32. КВАДРАТ. ПЕРИМЕТР КВАДРАТА Мета: навчити учнів розрізняти квадрат за істотними ознаками; вчити обчислювати периметр квадрата; розвивати пізнавальну активність, уміння спостерігати і порівнювати, робити висновки, висловлювати власну думку; виховувати культуру розумової праці. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ […]...
- Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, якщо: – дві його висоти […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Квадрат суми та квадрат різниці двох виразів 567. (5а + 3)2 = 25а2 + 30а + 9. 568. Тотожності: 3) (12а – b)2= 144а2 – 24аb + b2. Рівняння коренів не має. 577. (a – b)2 = (b – a)2 – тотожність, бо (a – b)2 = a2 – 2ab + b2; (b – a)2 = b2 – 2ab + a2, a […]...
- Правильні многокутники Геометрія Многокутники Правильні многокутники Опуклий многокутник називається Правильним, якщо в нього всі сторони рівні й усі кути рівні. Многокутник називається Вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається Описаним навколо кола, якщо всі його сторони дотикаються до деякого кола. Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним […]...
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Кут між мимобіжними прямими Геометрія Стереометрія Кут між мимобіжними прямими Дві прямі, що перетинаються, утворюють суміжні та вертикальні кути. Кутова міра меншого із суміжних кутів називається Кутом між прямими. Кут між перпендикулярними прямими дорівнює за означенням. Кут між паралельними прямими вважаємо таким, що дорівнює нулю. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним […]...
- РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...