Головна ⇒ 📌Довідник з математики ⇒ Метод інтервалів
Метод інтервалів
Математика – Алгебра
Границя
Метод інтервалів
Отже, нехай функція 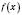 неперервна на інтервалі І й перетворюється на 0 у скінченній кількості точок цього інтервалу. Тоді інтервал І розбивається цими точками на інтервали, в кожному з яких
неперервна на інтервалі І й перетворюється на 0 у скінченній кількості точок цього інтервалу. Тоді інтервал І розбивається цими точками на інтервали, в кожному з яких 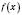 зберігає незмінний знак. Щоб визначити цей знак, достатньо обчислити значення
зберігає незмінний знак. Щоб визначити цей знак, достатньо обчислити значення 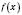 у будь-якій точці кожного такого інтервалу.
у будь-якій точці кожного такого інтервалу.
Приклад
Розв’язати нерівність 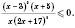
Розглянемо функцію
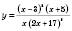 .
.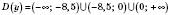 (див. рисунок):
(див. рисунок):
Знайдемо нулі функції
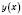 :
: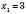 ,
, 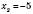 .
.Ці точки поділяють область визначення функції на інтервали, в кожному з яких функція зберігає постійний знак (див. рисунок):

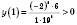 .
.Отже, для
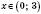 отримали
отримали 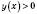 (ставимо на рисунку знак “+” над цим інтервалом).
(ставимо на рисунку знак “+” над цим інтервалом).Зверніть увагу: в умові
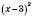 показник
показник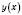 по різні боки від числа 3 однакові.
по різні боки від числа 3 однакові.Решта показників степеня – числа непарні. Тому, переходячи через точки 0; -5; -8,5, знаки змінюємо на протилежні.
Обираємо проміжки, над якими стоїть знак “-“. Нерівність нестрога, тому число -5 теж є розв’язком.
Відповідь:
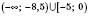 .
.Related posts:
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Властивості модуля – Модуль і його властивості Математика – Алгебра Модуль і його властивості Модуль числа – це відстань від 0 до точки, що відповідає цьому числу на координатній прямій, виміряна в одиничних відрізках. Отже, для всіх значень a. Властивості модуля 1. . 2. Якщо , то . 3. Якщо , то 4. Модуль суми скінченного числа дійсних чисел не перевищує суми […]...
- Степінь з натуральним показником Математика – Алгебра Одночлени Степінь з натуральним показником Степенем Числа a з натуральним показником n, більшим за 1, називається добуток n множників, кожний із яких дорівнює a. Тобто де a – основа степеня; n – показник степеня. Степенем числа a з показником 1 є саме число a. Знак степеня з натуральним показником 1. Якщо основа […]...
- Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...
- Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
- Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на якому функція визначена і для всіх із цього інтервалу. Точку називають Точкою максимуму функції, а саме число – Максимумом функції, якщо існує інтервал , , на якому функція визначена і […]...
- Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Узагальнення поняття степеня Математика – Алгебра Степенева функція Узагальнення поняття степеня Основнi означення 1. Якщо n Є N, , то , де a – довільне число. 2. , де а – довільне число. 3. для . не має змісту. 4. , n Є N, . 5. , n Є N, m Є Z, . Властивості степеня з раціональним […]...
- Дослідження властивостей функції і побудова її графіка Математика – Алгебра Похідна Дослідження властивостей функції і побудова її графіка Для того щоб дослідити функцію , треба: 1) знайти область визначення ; 2) знайти область значень ; 3) дізнатися про парність чи непарність функції ; 4) з’ясувати, чи є функція періодичною; 5) знайти нулі функції; точки перетину графіка з осями координат; 6) визначити проміжки, […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА ЗАДАЧІ НА ПОВТОРЕННЯ ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА 1. Скільки чисел натурального ряду розміщено між числами: 1)120 і 129; 2) 999 і 1100; 3)8901 і 8910; 4) 50000 і 50020? 2. На прямій дано три точки А, В і С. Знайдіть довжину відрізка ВС, якщо АВ = 8 см і АС – 9 см. Скільки розв’язків […]...
- Протилежні числа. Цілі числа. Раціональні числа Розділ 4 Раціональні числа і дії мідними §35. Протилежні числа. Цілі числа. Раціональні числа Точки A і B з відповідними координатами 2 і -2 однаково віддалені від початку відліку – точки О і знаходять ся по різні боки від неї (мал. 71). Щоб потрапити з точки О в точки A(2) і B(-2), треба відкласти однакові […]...
- Степінь натурального числа з натуральним показником Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 7. Степінь натурального числа з натуральним показником Уже відомо, що суму, в якій всі доданки рівні між собою, можна записати коротше – у вигляді добутку. Наприклад, У математиці є спеціальний спосіб і для запису добутку, в якому всі множники рівні між собою. […]...
- Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь з раціональним показником N ) Для будь-якого невід’ємного числа а й натурального числа n (n ≥ 2) існує одне невід’ємне число b, при якому bn = а й позначається . Звідси випливає: 1. = 0 тільки при а = 0; 2. = 1 тільки при а = […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- Квадрат і куб від’ємного числа Урок № 8 4 Тема. Квадрат і куб від’ємного числа Мета: повторити поняття квадрата та куба числа (степінь з натуральним показником) та з’ясувати властивості квадрата і куба від’ємного числа; продовжити роботу на удосконалення умінь виконувати додавання та множення раціональних чисел із використанням їх властивостей. Тип уроку: застосування знань, вмінь, навичок. Хід уроку I. Перевірка домашнього […]...
- СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ РОЗДІЛ II ОДНОЧЛЕНИ &5. СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ Подивіться на малюнки 3 і 4. Ви бачите квадрат зі стороною а (мал. 3) і куб з ребром а (мал. 4). Ви знаєте, як знайти площу квадрата й об’єм куба та як записати результат за допомогою відповідних виразів: а2 і а3. Узагалі, добуток n рівних множників, кожний […]...
- Степінь Математика – Алгебра Подільність натуральних чисел Степінь Добуток n однакових множників, кожний із яких дорівнює а, називається n-м Степенем числа А і записується : , де n – натуральне число. Вираз називається степенем, число a – основою степеня, число n – показником степеня. Приклади ; ....
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Лінійні нерівності та їхні системи УРОК № 61 Тема. Лінійні нерівності та їхні системи Тестове завдання 1. Знайдіть переріз проміжків (-6; 7] і (-4; 25]. А) [7; 25); б) [-4; 7); в) (-6; 25]; г) (-4; 7]. 2. Розв’яжіть нерівність . A) k < 1,125; б) k? ; в) k? 1,125; г) немає розв’язків. 3. При яких х має зміст […]...
- Розв’язування логарифмічних нерівностей УРОК 61 Тема. Розв’язування логарифмічних нерівностей Мета уроку. Формування умінь учнів розв’язувати логарифмічні нерівності І. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні цих завдань. II. Сприймання і усвідомлення розв’язування логарифмічних нерівностей (які розв’язуються введенням нової змінної) Приклад 1. Розв’яжіть нерівність log х – log5 […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- ЧИСЛО І ЦИФРА 9. ПОНЯТТЯ “ДЕВ’ЯТИЙ”. ДОПОВНЕННЯ ДО 9. ПОРІВНЯННЯ ЧИСЕЛ. НАПИСАННЯ ЦИФРИ 9. ЧИТАННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 31. ЧИСЛО І ЦИФРА 9. ПОНЯТТЯ “ДЕВ’ЯТИЙ”. ДОПОВНЕННЯ ДО 9. ПОРІВНЯННЯ ЧИСЕЛ. НАПИСАННЯ ЦИФРИ 9. ЧИТАННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ Мета: продовжити формування в учнів поняття “числа”, учити писати цифру 9; ввести поняття “дев’ятий”; учити порівнювати числа в межах 9, доповнювати до […]...