Головна ⇒ 📌Довідник з геометрії ⇒ Многогранники
Многогранники
Геометрія
Многогранники
Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, – ребром двогранного кута. Півплощини називаються Гранями двогранного кута.
Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається Лінійним кутом двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного кута.
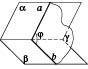
Міра двогранного кута не залежить від вибору
Побудувати лінійний кут двогранного кута можна двома способами.
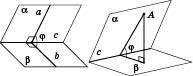
1. Обрати точку на ребрі кута й провести через цю точку перпендикуляри до ребра, що лежать у гранях кута (див. рисунок нижче зліва). Кут між цими перпендикулярами – лінійний кут даного двогранного кута.
2. Обрати точку на грані двогранного кута й опустити з неї перпендикуляри на ребро кута та на іншу грань двогранного кута (див. рисунок нижче справа). З’єднати основи цих перпендикулярів. Кут між цим відрізком і перпендикуляром, проведеним до ребра двогранного кута, буде лінійним кутом даного двогранного кута.
Related posts:
- Правильні многогранники 862. Якщо у піраміді всі ребра рівні, то з них можна скласти правильний октаедр. АB = а; AM = а; Відповідь: 863. А) так; б) так. 864. А) ні; б) так; в) ні. 865. Якщо з однієї вершини куба провести три діагоналі бічних граней і їх кінці з’єднати відрізками, то утворена піраміда буде тетраедром. 866. […]...
- Двогранні кути 520. Нехай дано двогранний кут, міра якого 60°, ∠AOB = 60°. AO + MN, BO + MN, АВ + β, АВ = 12 см. ΔАОВ – прямокутний. 521. Нехай дано двогранний кут, який дорівнює 45°. т. В? α, ОВ = 8 дм. АВ + β. Δ ΟΒΑ – прямокутний. 522. Нехай дано двогранний кут ∠BOA. […]...
- Описана піраміда Геометрія Комбінації геометричних тіл Описана піраміда Якщо вершина піраміди проектується в центр кола, яке є вписаним в основу піраміди, то центр вписаної кулі – точка перетину висоти піраміди з бісектрисою лінійного кута двогранного кута при ребрі основи. У будь-яку правильну піраміду можна вписати кулю, центр якої лежить на висоті піраміди. Точки дотику кулі й бічних […]...
- Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...
- Тригранні кути 562. Нехай дано тригранний кут, усі плоскі кути якого прямі. Лінійний кут кожного тригранного кута прямий, отже всі його двогранні кути прямі. 563. Якщо всі двогранні кути тригранного кута рівні, то кожний з них більше за 60°, оскільки ∠1 + ∠2 + ∠3 > 180°; ∠Α = ∠1 – ∠2 = ∠3, то 3∠A > […]...
- Многогранники 663. А) Грань – Г = 6; ребро – Р = 12; вершина – В = 8. Теорема Ейлера: В – Р + Г; 8 – 12 + 6 = 2. Б) Г = 5; Р = 9; В = 6. 6 – 9 + 5 = 2 В) Г= 7; Р = 12; В […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Кут між мимобіжними прямими Урок 53 Тема. Кут між мимобіжними прямими Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими. Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда. Хід уроку II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання. III. Сприйняття й […]...
- Многогранник Геометрія Многогранники Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників. Многогранник називається Опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини й поверхні опуклого многокутника називається Гранню. На рисунку нижче зліва зображений неопуклий многогранник; на рисунку справа – опуклий. […]...
- Конус Геометрія Тіла обертання Конус Круговим конусом називається тіло, яке складається з круга – Основи конуса, точки, яка не лежить у площині цього круга, – Вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються Твірними конуса. Конус називається Прямим (далі просто “конус”), якщо […]...
- Площа круга Геометрія Площі фігур Площа круга S =pR2 Круговим сектором називається частина круга, яка лежить усередині відповідного центрального кута (див. рисунок). Sсект, де – градусна міра відповідного центрального кута. Круговим сегментом називається спільна частина круга й півплощини. На рисунку нижче зліва зображений круговий сегмент, якщо ; на рисунку справа – круговий сегмент, якщо ....
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...
- Об’єми многогранників Геометрія Об’єми тіл Об’єми многогранників Об’єм будь-якої призми дорівнює добутку площі основи та висоти. . На рисунках наведені приклади призм із різними основами. Для прямокутного паралелепіпеда отримаємо , де a, b, c – його виміри. Для куба , де a – довжина ребра. Для похилої призми (рисунок нижче зліва) об’єм можна обчислити як добуток площі […]...
- Піраміди і зрізані піраміди 796. Нехай дано правильну чотирикутну піраміду, висота якої MO = 147 м, А площа основи – SABCD = 5,3 га = 53 000 м2. ∠MCO – кут нахилу бічного ребра. OK + ВС, MK + BC, ∠MKO – лінійний кут двогранного кута при ребрі основи піраміди. SABCD = 53 000 м2; ΔMOK – прямокутний. ∠MOK […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180° Геометрія Декартові координати на площині Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180° Візьмемо коло на площині Oxy з центром у початку координат і радіусом R. Відкладемо від додатної півосі Ox кут у верхню півплощину (див. рисунок нижче). Точку перетину сторони кута з колом назвемо . Вона має координати . Тоді […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Призми 701. Ні, не існує. 100-кутна призма має 300 ребер, 200 вершин. 703. Нехай дано правильну п’ятикутну призму, ∠ABC – двогранний кут при бічному ребрі ВВ1. ∠ABC – лінійний кут двогранного кута при бічному ребрі. ВВ1. Відповідь: 108 704. Нехай дано призму, бічне ребро якої АА1 = l, нахилене до площини основи під кутом α. ∠Α1ΑΟ […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 19. ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК Щоб розв’язувати складніші задачі на побудову, потрібно знати, що таке геометричне місце точок. Геометричним місцем точок (ГМТ) називають фігуру, яка складається з усіх точок, що мають певну властивість. Розглянемо кілька геометричних місць точок площини. Коло – геометричне місце точок, рівновіддалених від даної точки. […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
- Кут між прямою і площиною Урок 54 Тема. Кут між прямою і площиною Мета уроку: формування поняття кута між прямою і площиною, а також умінь учнів знаходити кути між прямою і площиною. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Дайте означення кута між мимобіжними прямими. 2) Чи залежить кут між мимобіжними прямими від вибору прямих, які […]...
- Циліндр, описаний навколо кулі Геометрія Комбінації геометричних тіл Циліндр, описаний навколо кулі Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...