Множини і підмножини
567.
А – (понеділок, вівторок, середа, четвер, п’ятниця, субота, неділя) – множина днів тижня;
В – множина кольорів світлофора: (жовтий, зелений, червоний);
С – множина материків: (Євразія, Африка, Північна Америка, Південна Америка, Австралія, Антарктида);
D – множина цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
E – множина кольорів веселки (червоний, оранжевий, жовтий, зелений, голубий, синій, фіолетовий).
569.
{А, В, Г, И, Л, О, Р, С}.
570.
{0, 1, 4, 9}.
571.
А) {0, 3, 6, 9} ? 3;
Б) {0, 5} ? 5;
В) {0} ? І5,
572.
А){?, ?}
Підмножини{?}, {?}, {?,
Б)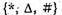 
{*, Δ, #}
Підмножини {*}, {Δ}, {#}, {*, Δ}, {*, #}, {Δ, #}, {*, Δ, #}
573.
{а, о, у, е, и, і}.
574.
А) {4, 5, 6, 7, 8, 9, 10, 11, 12};
Б) {-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
576.
60 ? {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}; 73 ? {1}
577.
D (120, 150) : {1, 2, 3, 5, 6, 10, 15, 30}.
578.
А) х(х2 – 4)= 0 {-2; 0; 2};
Б) х2 + 6 = 0 {Ø};
В)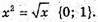 
579.
А) 2х – 1 < 7, x < 4, (-∞; 4);
Б) х2 -2х ≤ 0, х(х – 2) ≤ 0, [0; 2];
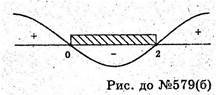
В) |x – 3| < 2, -2 <-х – 3 < 2, 1 < х < 5 (1; 5).
580.
А) 7 ? Q;
Б) -5 ? R.
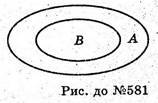
581.
Так, А – множина птахів; В – множина голубів.
582.
А) у =
Б) у = 1x, х? [1; 8], у = {1}.
583.
K = {a, b, c, 2}, P = {1, 2, a, c, x}.
Переріз K 
P = {a, c, 2},
K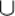 
P = {1, 2, a, c, x, b}.
P \ K = {1, x}; K \ P = {b}.
584.
A) A – {2, 3, 7}, В = {5, 7, 3},
A В = {3. 7}, A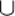 
В = {5, 7, 3, 2};
Б) A = {0, 1, 2}, В = {0, -1, 2, -3},
A В = {0, 2}, Α 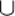В = {0, -1, 2, -3, 1};
В) A = {-, ^,?}, В = {^, 0, -},
A B = {^}, A 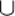B = {-, ^, ?, 0, -};
Г) A = {?, 0, ^}, В = {0, Δ, ?},
A В = {?, 0), A 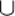В = {?, 0, ^, Δ}.
585.
A) A = {a, b, c}, В = {b, d},
A B = {b}, A 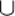В = {a, b, c, d};
Б) A = {α, β, γ}, В = {б, в, β, γ, г},
A В = {β, γ}, A 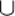В = {a, β, γ, б, в, г};
В) А = (3, 5, 7}, В = {7, 6, 5, 4},
А В = {5, 7}, А 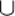В = {3, 5, 7, 6, 4};
Г) А = {2, 3},В = {22, 33},
А В = {Ø}, А 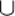В = {2, 3, 22,33}.
586.
А) множина від’ємних чисел, нескінченна;
Б) множина цифр у записі числа π, нескінченна;
В) множина чисел, що належать відрізку [0; 1], нескінченна;
Г) 2х + 3у = 5- множина розв’язків рівняння – нескінченна;
Г) множина розв’язків нерівності х2 – 2у + 1 ≤ 0 – нескінченна.
587 .
А) спільні дільники чисел 60 і 120: {1, 2, 3, 6};
Б) прості числа з першої сотні: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};
В) множина розв’язків рівняння x2 + у2 = 0 : {(0; 0)}.
588.
А) (-∞; 5) 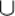(1; +∞) = (-∞; +∞); (-∞;5) 
(1; +∞) = (1; 5);
Б) (1; 3) 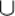[1; ,∞) = [1; ∞); (1; 3) [1; ∞) = (1; 3);
В) [0; 2] 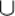(-∞; 0) = (-∞; 2); (-∞; 0) 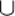[0; 2] = {Ø}.
589.
А) (-7; 7) 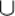(-∞>; -1) = (-∞; 7); (-7; 7) (-∞; -1) = (-7;-1);
Б) [0; 3) 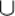[-3; 0] = [-3; 3); [0; 3) [-3; 0] = {0};
В) [4; ∞] 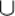[1; 2) = [1; 2) 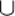[4; ∞); [4; ∞) 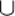[1; 2) = {Ø}.
590.
A – множина розв’язків рівняння 2х + 3у = 5,
В – множина розв’язків рівняння х – 5у – 9
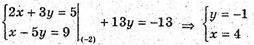
А В – {(4; -1)} – це точка перетину прямих А і В.
591.
A – множина чисел, кратних 2, тобто а = 2k,
В – множина чисел, кратних 3, тобто b = Зn, тоді переріз А В = {6m},
Тобто числа, кратні 6, ця множина нескінченна {6, 12, 18, .., 6m,…}.
592.
A – множина парних, натуральних чисел,
В – множина непарних натуральних чисел,
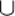Тоді переріз А В = {Ø}, об’єднання А В = N –
Множина всіх натуральних чисел, А\В = А.
593.
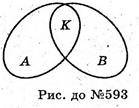
А – множина прямокутників,
В – множина ромбів,
К = А В – це квадрати
К А = К, К А = А, так
А\В – це прямокутники, які не є квадратами,
Тобто з різними сторонами;
В\А – це ромби, які не є квадратами,
Тобто кут ромба ≠ 90°.
594.
А) А – множина квадратних рівнянь,
В – множина рівнянь, які мають 2 корені;
Б) {Δ, ?, 0}
Двоелементні підмножини: {Δ, ?}, {Δ, 0},{?, 0}.
Всього 3 підмножини.
595.
А = {a, b, с, d)
Трьохелементні підмножини: {a, b, с}, {a, b, d}, {а, с, d}, {b, с, d}.
4 трьохелементних підмножин.
596.
А) множина, яка містить d елемент, має 2 підмножини: {а}, Ø;
Б) множина, яка містить 2 елементи, має 4 підмножини:
{a}, {b}, {а, b}, Ø, тобто 22 = 4;
В) три елементи – 8 підмножин:
{a}, {b}, {с}, {a, b}, {а, с}, {b, с}, {а, b, с}, Ø, тобто 23 = 8;
Г) чотири елементи – 16 підмножин:
{a}, {b}, {с}, {d}, {a, b}, {а, с}, {a, d}, {b, с}, {b, d}, {с, d},
{a, b, с}, {a, b, d), {а, c, d}, (b, с, d}, {a, b, с, d}, Ø, тобто 24 = 16.
597.
{a, b, с, d, е}
{a, b},{а, с}, {a, d}, {a, e}, {b, с}, {b, d}, {b, e}, {с, d}, {с, e}, {d, e}.
Всього: 10.
(a, b, c), {a, b, d}, {a, b, e}, {b, c, d}, {b, c, e}, {c, d, e}, {a, c, d},
{a, c, e}, {a, d, e}, {b, d, e}.
Всього: 10.
(1 votes, average: 5.00 out of 5)
Loading...